Законы подобия
И понял вдруг: нет времени.
На крыльях поднят как орел, я видел
сразу, что было и что будет,
Пружины троек видел я и двоек
В железном чучеле миров,
Упругий говор чисел.
И стало ясно мне
Что будет позже
***
Доски судьбы! как письмена черных ночей вырублю вас, доски судьбы!...Доски судьбы! читайте, читайте прохожие! Как на тенеписи, числа борцы пройдут перед вами, снятые в разных сечениях времени, в разных плоскостях времени, и все их тела, разных возрастов сложенные вместе, дают глыбу времени между падениями царств, наводивших ужас
Чистые законы времени строятся на степенях двойки и тройки, первых четном и нечетном числах: Мой основной закон времени: во времени происходит отрицательный сдвиг через 3n дней и положительный через 2n дней; события, дух времени становится обратным через 3n дней и усиливает свои числа через 2n дней
Прошлое вдруг стало прозрачным <...> Я понял, что время построено на степенях двух и трех <...> У пространства каменный показатель степени, он не может быть больше трех, а основание живет без предела; наоборот, у времени основание делается твердыми двойкой и тройкой, а показатель степени живет сложной жизнью, свободной игрой величин <...> событие, достигшее возраста 3n дней, меняет знак на оборотный <...> Как-то радостно думалось, что по существу нет ни времени, ни пространства, а есть два разных счета, два ската одной крыши, два пути по одному зданию чисел
Велимир Хлебников. И понял вдруг: нет времени
https://web.archive.org/web/20180715010425/https://kirsoft.com.ru/freedom/KSNews_982.htm
***

VIII. 2.3. Законы подобия
Внимательное изучение чисел, представленных в табл. VIII. 1, показывает, что их сходимость к точке накопления подчиняется простому и строгому закону: разность значений м, соответствующих двум последовательным бифуркациям, уменьшается каждый раз соответственно почти постоянному коэффициенту
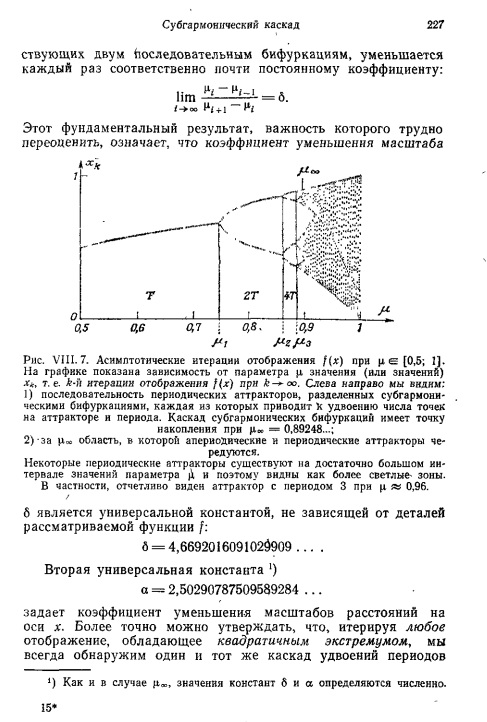
...Этот фундаментальный результат, важность которого трудно переоценить, означает, что коэффициент уменьшения масштаба Б является универсальной константой, не зависящей от деталей рассматриваемой функции:
Б = 4,6692016091029909....
Вторая универсальная константа ')
А = 2,50290787509589284...
задает коэффициент уменьшения масштабов расстояний на оси х. Более точно можно утверждать, что, итерируя любое отображение, обладающее квадратичным экстремумом, мы всегда обнаружим один и тот же каскад удвоений периодов с одними и теми же законами подобия, которые приведены выше. Мы располагаем весьма общей теорией, которая апостериори обосновывает наш выбор конкретной функции f. Замечательно, что эта теория позволяет делать количественные предсказания, если выполнено простое качественное условие (Хорошо известна аналогия между упомянутой теорией и теорией фазовых переходов, в частности процедурой и терминологией теории ренормгруппы. Константы Б и А можно рассматривать как «критические покаэатели» в точке накопления).
...
VIII. 3. ХАРАКТЕРИСТИКИ ХАОСА
VIII. 3.1. За субгармоническим каскадом при возрастании параметра М и его стремлении к М_безкон появляются аттракторы со все большим периодом 2^l. Следовательно, для того чтобы установить соответствующую периодичность, за явлением требуется наблюдать в течение все более продолжительного (бесконечно большого в точке М_безкон) времени. Но что происходит за точкой накопления?
Численное моделирование показывает, что за критическим значением М = 0,892486418... начинается очень сложная область. На графике, представленном на рис. VIII. 7, появляются различные зоны, одни более светлые, другие более темные. Подробный анализ обнаруживает, что в закритической области периодические аттракторы чередуются с режимом, который теперь принято называть хаосом.
В последнем случае итерации функции f порождают последовательность таких значений х, которые а) не повторяются, б) зависят от начального условия х0. В частности, две первоначально близкие точки порождают две последовательности итераций (или траекторий), которые расходятся друг от друга.
...
VIII. 3.3. Обратный каскад

Рис. VIII.10. Прямой и обратный каскады. Этот схематический рисунок приведен для того, чтобы привлечь внимание читателя к одной детали, которая не видна на рис VIII.7: обратный каскад — своего рода нечеткое отражение прямого каскада относительно вертикали, соответствующей значению параметра М_безкон.
Сказанное выше позволяет полагать, что хаотический режим при М > М_безкон не полностью лишен определенного порядка, хотя этот порядок на первый взгляд, возможно, и не виден. Другим элементом порядка, свидетельствующим о том же, являются «окна периодичности» (разд. VIII.3.4) — периодические аттракторы в интервале (М_безкон, 1). Некоторые из них можно наблюдать в виде более светлых зон) на рис. VIII. 7. Периодические и апериодические аттракторы тесно взаимосвязаны. Действительно, как показывает тщательный анализ апериодических аттракторов, они являются своего рода «шумовыми предельными циклами» с периодом 2^l, где l — целое число, неограниченно возрастающее, когда М стремится к М_безкон сверху. Более точно, образ
точки последовательно посещает множество, состоящее из 2^l непересекающихся отрезков из интервала (0, 1). После 2^l итераций мы возвращаемся на исходный отрезок: это позволяет говорить о цикле. Вместе с тем поведение внутри каждого отрезка полностью хаотическое: отсюда прилагательное «шумовой». Короче говоря, все итерации порядка 2^l содержатся внутри малого отрезка, но там они полностью неупорядочены. Аналогичное утверждение справедливо относительно каждого из 2^l отрезков.
При возрастании М мы видим, что при некоторых значениях этого параметра отрезки расщепляются на два. Вместо шумового цикла с периодом 2^l возникает другой шумовой цикл с вдвое меньшим периодом, т.е. с периодом 2^(l-1). При дальнейшем возрастании процесс повторяется до тех пор, пока не будет достигнут «период» 2^0 = 1. На рис. VIII. 10 схематично показана серия изменений периода. Мы видим, что наряду с субгармоническим каскадом существует другой каскад с близкой структурой, но ведущий в противоположном направлении по оси М. Обычно первый каскад принято называть прямым, а второй обратным. Результат, который но самым скромным оценкам может быть назван замечательным, состоит в том, что значения параметра М, при которых происходят бифуркации обратного каскада, также сходятся к М_безкон с тем же масштабным множителем Б = 4.669..., что и прямой каскад. В этом еще одно подтверждение того, что в хаосе существует некоторый порядок (если это утверждение нуждается в подтверждении)!
...
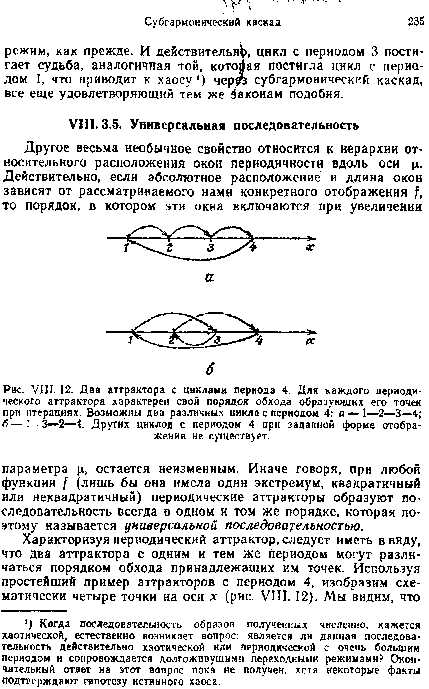
VIII.3.5. Универсальная последовательность
Другое весьма необычное свойство относится к иерархии относительного расположения окон периодичности вдоль оси М. Действительно, если абсолютное расположение и длина окон зависят от рассматриваемого нами конкретного отображения f, то порядок, в котором эти окна включаются при увеличении параметра М. остается неизменным. Иначе говоря, при любой функции f (лишь бы она имела один экстремум, квадратичный или неквадратичный) периодические аттракторы образуют последовательность всегда в одном и том же порядке, которая поэтому называется универсальной последовательностью.
Характеризуя периодический аттрактор, следует иметь ввиду, что два аттрактора с одним и тем же периодом могут различаться порядком обхода принадлежащих им точек...
Берже П., Помо И,, Видаль К. Порядок в хаосе. О детерминистском подходе к турбулентности. Пер. с франц. Юлия Данилова. М.: Мир, 1991. 366с.
https://zenodo.org/record/12813/files/berzhe_p_pomo_i_vidal_k_poryadok_v_haose_o_deterministskom_p.pdf

О Природе Дружбы
https://web.archive.org/web/20161214043110/https://sinsam.kirsoft.com.ru/KSNews_166.htm
Се ТрГлаве молiхомь Влiце а Мале

2.II.22
Ну, тащися, Сивка
Шара земного.
Айда понемногу!
Я запрег тебя
Сохой звездною,
Я стегаю тебя
Плеткой грезною.
Что пою о всём,
Тем кормлю овсом,
Я сорву кругом траву отчую
И тебя кормлю, ею потчую.
Не затем кормлю -
Седину позорить:
Дедину люблю
И хочу озорить!
Полной чашей торбы
Насыпаю овса,
До всеобщей борьбы
За полет в небеса.
Я студеной водою
Расскажу, где иду я,
Что великие числа -
Пастухи моей мысли.
Я затем накормил,
Чтоб схватить паруса,
Ведь овес тебе мил
И приятна роса.
Я затем сорвал
Сена доброго,
Что прочла душа, по грядущему чтица, -
Что созвездья вот подымается вал,
А гроза налетает, как птица.
Приятель белогривый, - знашь? -
Чья грива тонет в снежных горах.
На тучах надпись - Наш,
А это значит: готовлю порох
Ну, тащися, Сивка, по этому пути
Шара земного,
- Сивка Кольцова, кляча Толстого.
Кто меня кличет из Млечного Пути?
А? Вова?
В звезды стучится!
Друг! Дай пожму твое благородное копытце!
Очи Перуна
Я продырявил в рогоже столетий.
Вылез. Увидел. Звезды кругом
Правительства все побежали бегом
С хурдою-мурдою в руках (1921-1922)
Велимiр Хлъбников. Ну, тащися, Сивка. 2.II.22
https://web.archive.org/web/20161218041028/https://sinsam.kirsoft.com.ru/KSNews_164.htm
Зарей Венчанный...Впервые я нашел черту обратности событий через 3^5 дней, 243 дня. Тогда я продолжил степени, и росты найденных времен стал применять к прошлому человечества. Это прошлое вдруг стало прозрачным, и простой закон времени вдруг осенил его все. Я понял, что время построено на степенях двух и трех, наименьших четных и нечетных чисел. Я понял, что повторное умножение само на себя двоек и троек есть истинная природа времени; и когда я вспомнил древне-славянскую веру в чет и нечет, я решил, что мудрость есть дерево, растущее из зерна суеверия в кавычках. Открыв значение чета и нечета во времени, я ощутил такое чувство, что у меня в руках мышеловка, в которой испуганным зверьком дрожит древний рок. Похожие на дерево уравнения времени, простые как ствол в основании и гибкие и живущие сложной жизнью ветвями своих степеней, где сосредоточен мозг и живая душа уравнений, казались перевернутыми уравнениями пространства, где громадное число основания увенчано или единицей, двойкой, или тройкой, но не далее. Это два обратных движения в одном протяжении счета, решил я. Я видел их зрительно: горы, громадные глыбы основания, на которых присела, отдыхая, хищная птица степени, птица сознания, для пространства, и точно тонкие стволы деревьев, ветки с цветами и живыми птицами, порхающими по ним, казалось время. У пространства каменный показатель степени, он не может быть больше трех, а основание живет без предела; наоборот, у времени основание делается твердыми двойкой и тройкой, а показатель степени живет сложной жизнью, свободной игрой величин. Там, где раньше были глухие степи времени, вдруг выросли стройные многочлены, построенные на тройке и двойке, и мое сознание походило на сознание путника, перед которым вдруг выступили зубчатые башни и стены никому неизвестного города. Если в известном сказании Китеж-град потонул в глухом лесном озере, то здесь из каждого пятна времени, из каждого озера времени выступал стройный многочлен троек с башнями и колокольнями, какой-то Читеж-град. Такие ряды, как 1053 = 3^(3 + 3) + 3^(3 + 2) + 3^(3 + 1), где число членов равно основанию, показатель старшей степени дважды взятая тройка, а другие показатели убывают на единицу, или всем знакомое число 365 = 3^5 + 3^4 + 3^3 + 3^2 + 3^1 + 3^0 + 1, с одной стороны вскрывали древнее отношение года к суткам, с другой стороны древнему сказанию о Китеж-граде давали новый смысл. Город троек со своим башнями и колокольнями явно шумел из глубины времени. Стройный город числовых башен заменил прежние пятна времени. Я не выдумывал эти законы: я просто брал живые величины времени, стараясь раздеться до нага от существующих учений, и смотрел, по какому эти величины переходят одна в другую. И строил уравнения, опираясь на опыт. И числовые скрепы величин времени выступали одна за другой в странном родстве со скрепами пространства. И в то же время двигаясь по обратному течению
Велимiр Хлъбников. Доски Судьбы
https://web.archive.org/web/20161218041028/https://sinsam.kirsoft.com.ru/KSNews_151.htm
Пусть f(x) = 1 – x. Тогда f(f(x)) = 1 – (1 – x) = x, причём f(1/2) = 1/2, и равенство f(x) = x выполнено только при x = 1/2. Точку 1/2 называют неподвижной точкой отображения f (или точкой периода 1), а все остальные точки — точками периода 2.
Вообще, для функции f(x) можно рассмотреть её итерации f(f(x)), f(f(f(x))), f(f(f(f(x)))),... и спросить себя, существуют ли числа x, для которых, например, f(f(f(x))) = x (точки периода 3). Теорема украинского математика Шарковского (1964) утверждает, что если упорядочить натуральный ряд некоторым специальным образом (как именно — объяснено ниже), то для любого натурального числа n, для любого натурального числа m, расположенного в рассматриваемом упорядочении правее, чем n, и для любого непрерывного отображения f прямой в себя, обладающего точкой периода n, отображение f будет обладать и точкой периода m. (Следствие. Если отображение имеет точку периода 3, то оно имеет периодические точки всех периодов правее)
Упорядочение натурального ряда, используемое в теореме Шарковского, устроено так:
сначала идут простые числа (кроме 2) 3, 5, 7, 11, 13, 17...;
затем простые числа, умноженные на два: 6, 10, 14, 22, 26, 34...;
затем простые числа, умноженные на четыре: 12, 20, 28, 44, 52, 68...;
затем простые числа, умноженные на восемь: 24, 40, 56, 88, 104, 136...;
...,
наконец, степени двойки:..., 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2, 1.
3<5<7<11<13<17<...<2^3<2^5<2^7<2^11<2^13<2^17...<2^2*3<2^2*5<2^2*7<2^2*11<2^2*13<2^2*17...<2n<2n-1...<2<1
Доказательство теоремы опирается на теорему о среднем значении непрерывной функции и состоит в поиске периодической точки замкнутых путей в ориентированном графе
А.Н. Шарковский. Сосуществование циклов непрерывного отображения прямой в себя / Укр. матем. журнал 1964 - Т.16. с.61-71
А.Н. Шарковский. О циклах и структуре непрерывного отображения / Укр. матем. журнал 1965 - Т.17. с.101-111
А.Н. Шарковский, С.Ф. Коляда, А.Г. Спивак, В.В. Федоренко. Динамика одномерных отображений. Киев: Наукова думка, 1989. c.216

Порядок Шарковского
Исследуя унимодальные отображения, украинский математик А.Н. Шарковский в 1964 г. обнаружил, что в области - хаоса - имеются так называемые - окна периодичности - узкие интервалы значений параметра r, в которых существуют периодические движения. Двигаясь вспять (т.е. в сторону уменьшения) по параметру r, можно наблюдать окна периодичности с периодами, равными соответственно
3-->5-->7-->11-->13-->17-->…
-->3*2-->5*2-->7*2-->11*2-->13*2-->17*2-->…
-->3*2^2-->5*2^2-->7*2^2-->11*2^2-->13*2^2-->17*2^2>…
...
-->2^n-->2^(n-1)-->...-->2^5-->2^4-->2^3-->2^2-->2-->1
(2.15)
(стрелка --> означает - влечет за собой: a --> b означает: а влечет за собой b, или b следует за а). В верхней строке представлены в порядке возрастания все простые числа, кроме 2, во второй строке - произведения простых чисел на 2, в третьей - произведения простых чисел на 2^2, в k-й строке сверху - произведения простых чисел на 2^k. Наконец, в последней (нижней) строке представлены чистые степени двойки. Двигаясь в нижней строке против направления стрелок от 1, мы проходим каскад удвоений периодов Фейгенбаума.
Самым - многообещающим - в порядке Шарковского оказывается 3-цикл. К аналогичному результату независимо от Шарковского пришли в 1975 г. Т. Ли и Дж. Йорк. Им также удалось показать, что из существования в унимодальной системе 3-цикла следует существование хаотических последовательностей, - цикл три рождает хаос. Ни теорема Шарковского, ни работа Ли-Йорка ничего не говорят об устойчивости циклов (окон периодичности).
Юлий Данилов. Лекции по нелинейной динамике. Элементарное введение. Серия "Синергетика: от прошлого к будущему". Изд.2, 2006. 208с.
https://www.urss.ru/cgi-bin/db.pl?cp=&page;=Book&id;=29805⟨=Ru&blang;=ru&list;=Found#FF0
https://vk.com/doc345514291_571666264
Ведь мы Русичи - славьте Богов наших!
Се бо сьме Русiще
Славце Бзе нашя
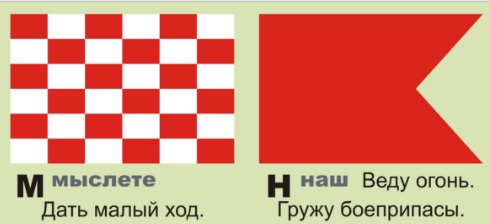
Сигнальные флаги ВМФ Российской Федерации. Буквенные сигналы. М, мыслете. Дать малый ход; Н, Наш. Веду огонь. Гружу боеприпасы (взрывчатые или огнеопасные вещества. - 14 июня 1905 на эскадренном броненосце Князь Потемкин-Таврический вместо специального красного флага, которого не было, был поднят сигнальный флаг из корабельного комплекта - красное полотнище с двумя косицами)
Во Влескниге слово Наш встречается более 427 раз.
Есть Наши (Слва Бзем нашем), а есть Чужие (а тоi Асклд пожере богом чюжем неботе нашiем; i не соуте нашiе нiжде цiзы кнзiе; i тако ряхомь бендетце цюже онь iнiу). Есть также Оные, а есть Иные.
Наши Боги (Бзе наша, Бъзi наше, Бозе наше, бяхом ста со Бзех нашех а до све Бзе не нуте наше) - 30
Наши ПраЩуры (ПраЩуры наша, Праштырь, Щуре нашiе) - 15
Наши Деды (ПраДы нашы, Прадi наше, Дядi нашi, наше Дiдо, Дядь наше ДажБо) - 9
Наши Отцы (ПраСвнтОце наша, ПраОтцi наша, наше СтарОцтсво, Парце наше, ОцЪм нашiм, нашi Оцi, Отце наше, Отще бо наш) - 49
Наш Род (род наше, наше родiще, нашiе родiцiе, старще родце нашiе) - 9
племы нашя, нашы людi (3), народо наш
Наши братья (брачке наше, наша братчi, брате нашiе, братрем нашiемо, до братень нашiех) - 7
Наши дети (дЪцкЪм нашiм, детем нашем, оце децко а мате нашя) - 5
жены нашiе, красене нашiа, сыны нашiе, дцере нашiа, о внуче нашiя, потомiцьЪ нашья
ТрГлаве наше, Сврг наш (3), до Рае наше, Суньце наше, Слонце Суне нашiу, Пероуньiе нашь, ДiдДубСноп нашь, Дiде наше ДажБо, ДажьБа ншiго, ДажБу нашоi, нашь Пъкрвiтел а Застоупiщ, i семы о Бзех внуще Iсьвра нашiе а ДажБо, КiОце нашье, Ярове наше, Вынего Допоменце нашего, нашен Iнтра
Наша Земля (земе наше, земi нашiеi, в нашi земЪ, земле наше) - 41
Наша кровь (крявь наше, кревь нашiе) - 6
Наша Русь (Русь наше, Русь тая есь Мать наше, Рускень нашiу) - 3
ступы нашiя (5), рiекы нашiе (2), краiе нашех (2), домове наша, до огнiцы нашiе, сонма наше, тржiща наше (2), граде нашiе, селы нашы, до жiтенець нашiех, кмЪто наше, поле нашi (2), жнева нашы (2), жiтва нашаiя (3), трвы нашея, Колуне нашю, Суренже наше
Наши (наша, нашiя, наше, нашь, про наше, iмоуть нас взеце нашiе, се бь годьштя земь iе нашя, бодЪ наше) - 12
А рцемо влiка Слву ОцЪм ншiм ДЪдом яковi соуте бе Сврзе Прщемо тако трiще а iдемо стд ншiх ведмо iа на трвiе
Наши враги (врзi наша, од врг нашех) - 15
Наш друг (наше друг) - 2
Наши князья (кънязi наша, конязi старощi наша, коненнзе нашiе, о прве Бане наше) - 10
вутце наше (3), воявенде нашы (3), наше рате (3), о меще нашiем (4), акыне наше, наше вое, валiцу нашiу, походiу нашiу, стенга нашя (4), крепе нашю, кромы нашя (2), нелегносте нашiю, владь наше, i ДежДе прiнесе побiедоу нашiу
Наша Слава (слва наше) - 3
Наши герои (гордiну нашего, грде нашie) - 4
нашiа стара потщiна, нашь пысьма, пъснеща наша, спiевы нашiе, бранды наша а боянi, паменте нашiе, свенты нашiа, жартве нашiе (3), волка нашя, вiре наше, дълженсте наше, наше мета, розумство нашiе, до мысля наша (2), наше борьба
Наша сила (сыла нашя, сiлоу нашю а кренпосць двужiла) - 7
Наша жизнь (жiвото нашо, наше жiвоте, о жiвоте нашем, за жiву нашу, о жiтнЪ нашя, до концiе жiтьбы нашiеа) - 15
Наша смерть (о смрте нашiе)
Наш труд (труды наше, труд наш) - 4
Наш хлеб (хлб нашь)
Наши души (душi наша, душi а телесi наша) - 6
Наши тела (тiелесы нашiа) - 3
Наши раны (вране нашiе)
Наше сердце (средьця наша, средьце наше, сердiе нашiе) - 5
Наше счастье (наше щества)
Наш скот (скуфе наше, скотi наша, о скоть нашоу, теле овна а скътiе наша, говiяд нашех, i кравiе нашiе скуте, теле овна а скътiе наша) - 8
краве наше (2), млеко нашiе на прпыте нашiе, млекы нашiа, покоръм наш, комонезем нашiм
ощесы нашiя, ренцы нашя, кренке наша (2), лядвы нашя, щерве нашiе, у мысце нашя
наше благо (3), о помоще нашiу, нуже нашiе, о захць нашiе, собьство нашiе, злыа дЪяня нашiя, о наше леносте, наше ошыбiце, скорбень нашу, нашiе роздiеляны i оусобiць, погенбель наше, нерадЪнем нашiiм, наше нещастъ, а прящехомсе зуре протi борства нашiего
Наши дни (дне нашiя, на щасе нашiе, до нашiе доба) - 8
будоущая нашя, о едноце нашiе - будущее наше, о единстве нашем
I се молiхь Бзе о заступнене нашiе - И я молил Богов, чтобы заступились за нас
од Оpie То се обящi нашы Оце со Борусоi - От Ория. Это ведь общий наш Отец с Борусами
А умре а до луце Свргова iде а тамо Перунiца рЪще Тые бо нiкiе iн нiже Рус гордiн а нi Грьць а нi вряг анмо Славен роду Славна А тон iде по спъвех Матыревеха МатыреСваНщех до луце твех Сварже влiке - А умрет — и на луга Свароговы идет, а там Перуница речет: „Ты ведь никто иной, а Рус-герой, а не Грець и ни воряг, а славный роду славного". И он идет вослед за пением Матеревым, Матери Всех Наших, на луга твои, Свароже великий!
Се бо словiесы нашя iстьве соуте i iхова леждена Се бо лузь рещашуть i неiа iмуть - Вот ведь, слова наши истинны, а их — лживы. Они ведь ложь рекут, и её и имеют
Се бо дружына собiрхом ста до стенга нашя - Вот ведь, дружины собрали мы с вами под стяги наши
Матере Слава бiе крыдлема о палы а iдьмо до стегi нашенстве А те бо Стенгi Ясуне - Матерь Слава бьет крыльями о полы, и идем под стяги наши, а они ведь — Стяги Ясные
Да iде слво Нашiе о Правдiе - Да идет слово наше к Правде