Теория графов
I. Основные определения
Пусть задано множество точек (на плоскости) -X и множество линий (отрезков), соединяющих все или некоторые точки - U.
Пара множеств X и U называются графом: G = (X,U). Элементами графа являются точки и соединяющие их линии (отрезки).
Точки графа называются вершинами. Линии (отрезки) могут быть направленными, то есть имеющими начало и конец, и ненаправленными.
Ненаправленные линии графа называются ребрами. Граф, состоящий из вершин и ребер, называется неориентированным графом.
Направленные линии графа называются дугами (и обозначаются линиями со стрелками). Граф, состоящий из вершин и дуг, называется ориентированным графом.
Граф, состоящий из вершин, ребер и дуг (то есть направленных и не направленных линий) называется смешанным.
Форма ребер и дуг не имеет значения. Главное, - какие вершины они связывают. Частный случай: дуга, у которой начало и конец совпадают, называются петлей. Ребра и дуги должны соединять вершины (и не могут обрываться «в некуда»).
Граф, состоящий только из одних вершин, называется ноль – графом. Пустой граф, граф у которого множество вершин (а следовательно и множество соединяющих их отрезков) - пустое множество.
Примеры графов: родословное дерево, карта дорог, схема соединений электрических или логических элементов, графическое изображение алгоритма, схема передвижения товаров или денежной массы.
Подграфом G' графа G=(X,U) называется граф, в котором входят часть его вершин и отрезков, то есть G'=(X',U') где X'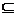 
X, U' 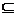U.. Остовным (частичным) графом G" пo отношению к графу G=(X,U), называется граф, содержащий все вершины графа G и часть отрезков графа G, то есть G"=(X,U'), где 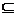U' U.
|
|
 |
Например, граф G
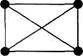
подграф
частичный граф
Частичный граф — частный случай понятия подграф.
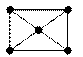
Подграф G''' = (X',U'), в который входят все линии (отрезки) графа G принадлежащие U и соединяющие вершины, принадлежащие X', называется подграфом, порожденным подмножеством X'.
| Граф | Множество вершин | Множество линий |
| 
| 
|
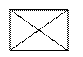
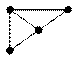
| Подмножество вершин X’ | Граф, порожденный подмножеством X’ | Граф, не является порожденным подмножеством X’ |
| 
| 
|
Допустима другая терминология:подграф – часть графа, частичный (остовной) граф – суграф, подграф, порожденный подмножеством вершин — подграф.
Звездный граф по отношению к вершине х - граф, содержащий все смежные х вершины и все инцидентные х - ребра, то есть включает все линии с началом и концом в вершине х.
 
|
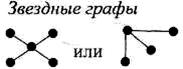
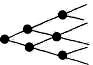Граф может быть конечным (если множество элементов графа конечно) и бесконечным.
Бесконечный граф
Граф, в котором любая вершина соединена с каждой другой вершиной, называется полным, иначе не полным.
полный не полный
|
Двудольным графом называется граф, у которого множество вершин можно разбить на два подмножества так, что любой отрезок (ребро или дуга) соединяет вершины из разных подмножеств.
Если каждая вершина одного из подмножеств соединена с каждой вершиной из другого подмножества, то такой граф называется полным двудольным графом.
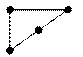
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что его дуги или ребра не пересекались.
Планарный граф - может быть изображен
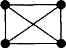
Простейшие непланарные графы:
|
|
 
|
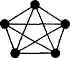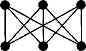
| полный граф (п=5) |
полный двудольный граф 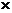3 
3.
Любой более простой граф (например, если изъять у них по одному ребру или вершине) – планарный. Граф, включающий в себя простейшие непларные графы – непланарный.
Теорема Эйлера: п-т+r=2, где п - число вершин, т - число ребер, r -число областей, ограниченных ребрами, включая внешнюю область. Если ребра пересекаются, точка пересечения должна трактоваться как вершина.
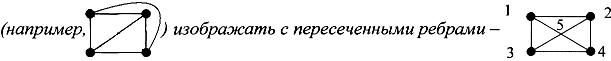При изображении непланарного графа (а в ряде случаев и планарного графа) допускается, чтобы ребра и дуги пересекались. При этом точка пересечения может вершиной не являться. Иногда удобно планарный граф,
1,2,3,4 – вершины, точка 5 вершиной не является. При этом вершины необходимо выделить (кружочками или жирными точками).
Операции над графами. Пусть G1= (X1,Ul), G2 = (X2,U2).
G = G1 
G2 = (X1 X2 , U1 U2) – объединение графов.
G = Gl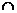 
G2 =(X] 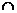X2,U1 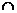U2) – пересечение графов.
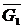– дополнение G1 до G (G1 
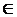G) - множество ребер и вершин, принадлежащих G, но не принадлежащих G'.
Следовательно, 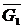– графом может не являться.
II. Характеристики ориентированного графа
Итак, ориентированный граф - граф, состоящий из вершин и дуг, то есть направленных отрезков, соединяющих две вершины.
Дуга u = (а,b)
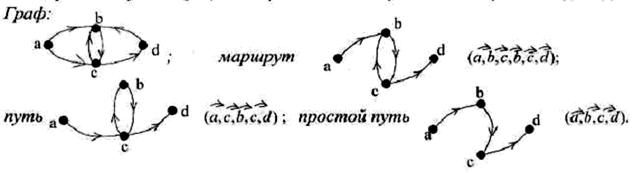
Маршрут – последовательность дуг, в которой конец каждой дуги совпадает с началом следующей дуги, то есть маршрут
μ = (u1,u2,…un) = (а0,a1…аn), где u1=(а0а1), и2=(а1а2)...
Путь – маршрут, в котором никакая дуга не встречается дважды. Если существует путь из вершины х в вершину у, то говорят, что вершина у достижима из х.
Простой путь - путь, в котором никакая вершина не встречается дважды.
|
|
Длина пути: существует два подхода.
1. Считается, что длина любой дуги равна единице (единичные дуги). Тогда длина пути равна числу дуг, составляющих путь. (В повседневной жизни иногда длина пути меряется числом трамвайных остановок или числом дневных переходов и т.д.).
2. Каждой дуге приписывается число e(иi) - длина дуги. (Это может быть расстоянием, временем проезда из точки в точку, стоимостью проезда и т.д.). Тогда длина пути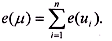 
Замкнутый маршрут – маршрут, у которого начальная и конечная вершины совпадают.
Контур – замкнутый маршрут, в котором никакая дуга не встречается дважды, то есть путь, в котором начальная и конечная вершины совпадают.
Простой контур – контур, у которой все вершины различные (за исключением конечной и начальной, которые считаются одной вершиной). Вместо введенных определений возможны и другие подходы:
| Введенные определения | Допустимые определения | |
| маршрут | маршрут | путь |
| путь | маршрут | простой путь |
| простой путь | путь | элементарный путь |
| замкнутый маршрут | замкнутый маршрут | контур |
| контур | замкнутый маршрут | простой контур |
| простой контур | контур | элементарный контур |
Элементарный контур еще можно определить как контур, не содержащий внутри себя других дуг и вершин. Частный случай контура - петля («контур единичной длины»), хотя часто петля контуром не считается.
Две вершины называются смежными, если существует дуга, соединяющей эти вершины.
Дугу называют инцидентной вершине, если она заходит в эту вершину или исходит из неё.