При пересечении двух плоскостей, также как и при пересечении прямой и плоскости, возможны следующие случаи:
РÇq= l
1. Обе плоскости проецирующие.
2. Одна плоскость проецирующая, другая общего положения.
3. Обе плоскости общего положения.
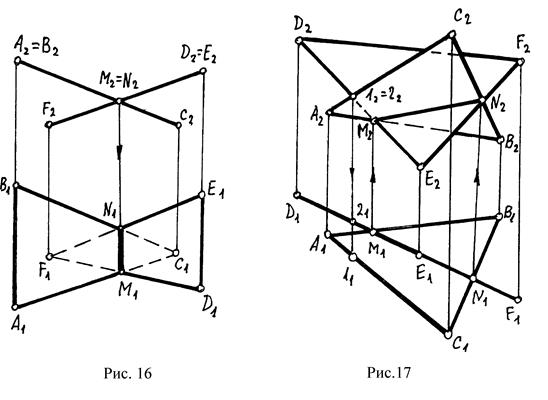
Случай 1: При пересечении плоскостей получается прямая линия. Проекции этой прямой совпадают с проекциями проецирующих плоскостей на основании их собирательных свойств. Проекции такой прямой уже имеются на комплексном чертеже и, следовательно, на требуется никаких дополнительных построений (рис.16).
Случай 2: Пересекаются плоскость общего положения с проецирующей плоскостью, то, как уже говорилось раньше такие задачи решаются по следующей схеме:
1. Формулируются собирательные свойства проецирующей плоскости.
2. Одна проекция линии пересечения совпадает с главной проекцией проецирующей плоскости.
3. Недостающая проекция линии пересечения строится из условия принадлежности к плоскости общего положения.
4. Определяется взаимная видимость (рис.17).
Случай 3: При построении линии пересечения двух плоскостей общего положения необходимо вводить вспомогательные плоскости (посредники). Так как в результате пересечения получается прямая линия, а прямая линия определяется в пространстве двумя точками, то и посредников требуется не меньше двух.
Рассмотрим построение линии пересечения двух плоскостей общего положения на примере.
Плоскость Р задана двумя пересекающимися прямыми, а и b, плоскость Q – двумя параллельными прямыми, e и d. Требуется построить линию пересечения плоскостей Р и Q.
Схема решения позиционной задачи №2 (случай 3):
1. Пересечем данные плоскости Р и Q вспомогательной горизонтальной плоскостью уровня l (l2).
2. Построим линии пересечении плоскости l с заданными плоскостями: lÇР= l (А, В), lÇQ=n(C, D).
3. Найдем точку пересечения построенных прямых l Çn=k. Точка K принадлежит одновременно обеим заданным плоскостям и Р, и Q, следовательно, точка K принадлежит линии пересечения заданных плоскостей.
4. Вводится вторая вспомогательная горизонтальная плоскость уровня D (D2). При помощи плоскости D находится вторая точка F, которая принадлежит линии пересечения.
5. Прямая m линия пересечения плоскостей P и Q проходит через точки K и F (рис.18).
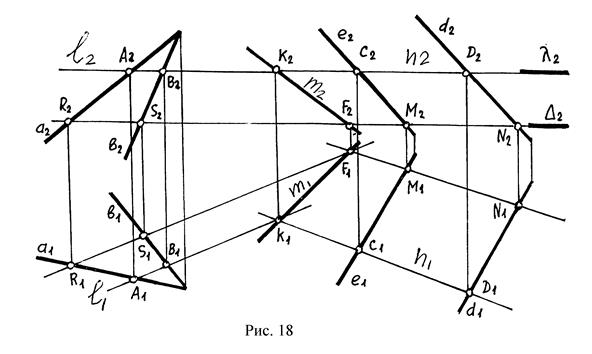
В качестве вспомогательных секущих плоскостей (посредников) можно выбирать любые проецирующие плоскости.
9. Способы преобразования чертежа. Основные задачи преобразования.
Задачи, в которых требуется определить метрические величины углов, длин, площадей, называются метрическими задачами. Решение таких задач значительно упрощается, если заданные на исходном чертеже геометрические образы занимают частные положения (т.е. параллельны или перпендикулярны одной из плоскостей проекций).
В случае, когда геометрические образы расположены в общем положении, возникает необходимость преобразования комплексного чертежа. Цель преобразования – придать геометрическим образам такое частное положение, которое позволяет упростить решение поставленной задачи.
Наиболее часто применяется при решении задач два способа преобразования комплексного чертежа: замена плоскостей проекций и плоскопараллельное перемещение.
При изучении способа плоскопараллельного перемещения важно уяснить следующие основные положения:
1. Плоскости проекций неподвижны, а оригинал перемещается в пространстве;
2. Все точки оригинала перемещаются во взаимно параллельных плоскостях уровня (каждая в своей плоскости).
Если рассматривать плоскопараллельное перемещение прямой или плоскости, то важно учитывать, что в процессе перемещения геометрического образа не изменяется угол его наклона к той плоскости проекций, относительно которой совершается его плоскопараллельное перемещение.
Из выше сказанного следуют основные правила построения комплексного чертежа:
1. Проекция оригинала на плоскости, параллельно которой совершается его движение, сохраняет свою форму и величину, изменяя только положение.
Проекции точек оригинала на другой плоскости проекций перемещаются по прямым, перпендикулярным соответствующим линиям связи (при этом проекция оригинала на эту плоскость меняет свое положение и форму).
При изучении способа замены плоскостей проекций важно понять, что при этом способе оригинал остается неподвижен, а одна из плоскостей проекций заменяется на новую, перпендикулярную к незаменяемой плоскости проекций и расположенную частным образом относительно оригинала. При замене одной из плоскостей новой плоскостью расстояние от точек геометрического объекта до незаменяемой плоскости проекций остаются постоянными. Следовательно, на комплексном чертеже присутствие осей между двумя заданными плоскостями проекций, а также между вновь введенной плоскостью и той, которая осталась обязательной.
Для того чтобы понять, как осуществляется построение на комплексном чертеже при замене плоскостей проекций по отношению к объекту, нужно понять, как происходит замена плоскостей проекций по отношению к точке. Пусть дана точка А (А1,А2) в заданной системе плоскостей проекций П1/П2 (рис.19). Первоначально заменим плоскость П2 на новую плоскость П4 (П4^П1). Помня о том, что линии связи всегда перпендикулярны координатным осям проводим А1А4^X14. Для построения точки А в П4
замеряем расстояние её до незаменяемой плоскости проекций П1, которое снимаем на П2 (от А2 до X12). Затем заменяем плоскость П1 на П5 (П5^П4), П4 в данной замене выполняет роль неподвижной (незаменяемой) плоскости. Плоскости П4 и П5 разделяет ось X45. Для построения точки А в П5 проводим аналогичные рассуждения, что и для построения точки в П4, расстояние точки А до незаменяемой плоскости проекций П4 замеряется на П1 и равно расстоянию от А1 до X14.
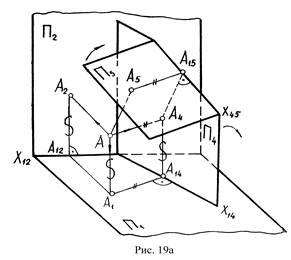

Изучив и запомнив основы способов замены плоскостей проекций и плоскопараллельного перемещения, следует научиться решать этим способом основные задачи преобразования комплексного чертежа (табл.2 и 3).
Для способов преобразования комплексного чертежа характерны следующие преобразования в отношении геометрических объектов:
1. Прямая общего положения может быть преобразована в линию уровня.
2. Линия уровня преобразуется в проецирующую прямую.
3. Плоскость общего положения сначала преобразуется в проецирующую плоскость.
4. Проецирующая плоскость может быть преобразована в плоскость уровня.
Способы преобразования комплексного чертежа применяются при решении следующих задач:
1. Первая задача – перевод прямой общего положения в прямую уровня. Такая задача решается с целью определения натуральной величины отрезка прямой линии и углов её наклона к плоскости проекций.
2. Вторая задача – перевод прямой уровня в проецирующую прямую. Цель решения задачи заключается в определении натуральных величин расстояний от точки до прямой, между параллельными прямыми, между скрещивающимися прямыми; определение натуральной величины двугранного угла (угла между плоскостями).
3. Третья задача – перевод плоскости общего положения в проецирующую плоскость. Область применения задачи – определение натуральной величины углов наклона плоскости к плоскостям проекций, упрощение определения расстояния от точки до плоскости между параллельными плоскостями, упрощение решения задач на взаимное пересечение линии и плоскости, а также плоскости и двух поверхностей.
4. Четвертая задача – перевод проецирующей плоскости в плоскость уровня. Решение необходимо для определения истинного вида плоской фигуры, определение её метрических размеров, выполнение различных геометрических построений в плоскости фигуры.
Таблица 2.

Научившись решать четыре основные задачи преобразования комплексного чертежа, можно приступить к решению любых метрических задач начертательной геометрии. Все метрические задачи можно разделить на три основные группы: определение расстояний, определение углов, определение натурального вида плоских фигур и разверток поверхностей.
Эти задачи имеют широкое распространение при решении практических задач, при проектировании изготовления деталей и сборочных машин и механизмов.
Таблица 3.

10. Кривые линии и их проекционные свойства
10.1. Общие сведения о кривых
Кривая – это множество точек пространства, координаты которых являются функциями одной переменной. Термин «кривая » в начертательной геометрии рассматривается как траектория, описанная движущейся точкой, как проекция другой кривой, как линия пересечения двух поверхностей и т.д.
Кривая называется плоской, если все ее точки принадлежат некоторой плоскости, в противном случае она называется пространственной. Примером плоской кривой может служить окружность, так как все ее точки размещаются в одной плоскости. Пример пространственной кривой - винтовая линия (рис. 20). К кривым второго порядка относятся: окружность, эллипс, парабола, гипербола. Это все плоские кривые. Если кривая 2-го порядка пересекается с прямой линией или плоскостью, то она не может давать более 2-х точек пересечения. Это ее отличительный признак, выраженный на языке начертательной геометрии. Кривая линия моделируется на плоскость проекций парой кривых.


Проверить плоская это кривая или пространственная можно с помощью 3-х точек А, В, С. Проекции точек должны лежать на проекциях кривой и располагаться на одной линии связи, или необходимо соединить попарно двумя прямыми линиями 4 произвольные точки этой кривой (рис. 21). Если эти прямые окажутся пересекающимися, то заданная на комплексном чертеже кривая – плоская, если скрещивающимися - пространственная. К пространственным кривым относятся все кривые, полученные при пересечении кривых поверхностей.
Кривые линии подразделяются на алгебраические, которые можно задать алгебраическими уравнениями (окружность, эллипс, парабола, гипербола др.) и трансцендентные, уравнение которых имеет вид трансцендентных функций (синусоида, спираль Архимеда и др.).
Важно уметь у алгебраических кривых определить порядок кривой – степень ее уравнения. Порядок плоской кривой геометрически определяется как максимально возможное число точек пересечения кривой с прямой линией, порядок алгебраической пространственной кривой – как максимальное число точек пересечения кривой с плоскостью. Например, прямая линия может пересекаться с эллипсом не более чем в 2-х точках. Отсюда эллипс – кривая второго порядка и его уравнение второй степени.
10.2. Особые точки кривых
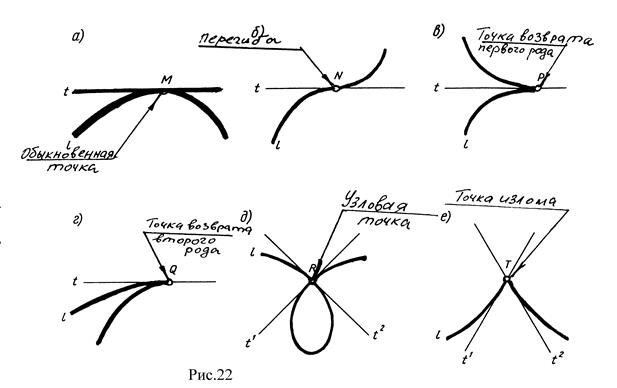
Точки кривых разделяются на обыкновенные (рис.22а) и особые (рис.22б, в, г, д, е). На рис. 22б точка N – точка перегиба, на рис. 22в точка Р – точка возврата первого рода, на рис. 22г точка Q – точка возврата 2-го рода, на рис. 22д точка R – узловая точка, на рис. 22е точка Т – точка излома.
Для характеристики точек плоской кривой необходимо наличие одной проекции кривой, а чтобы судить о характере точек пространственной кривой необходимо наличие двух проекций этой кривой.
10.3. Секущая, касательная, нормаль к кривой
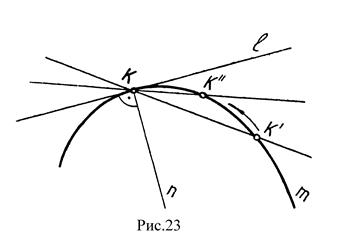
Прямая, пересекающая кривую в одной, двух и более точек называется секущей (рис. 23 – КК/). Касательной прямой ℓ к кривой m, в некоторой точке К является предельное положение секущей КК/, при котором точка К/ стремится к точке К. Прямая n проведенная через точку К перпендикулярно к касательной ℓ называется нормалью (рис.23). Причем, если прямая касается кривой в пространстве в некоторой точке К, то проекции этой прямой касаются проекций кривой в точках, которые являются проекциями точки касания (рис.21). На практике при анализе плоских кривых необходимо уметь строить касательную из точки, лежащей вне кривой, и через точку, взятую на кривой линии.
Для построения касательной, проведенной из точки вне кривой (рис.24), проведем из точки А пучок секущих, пересекающих данную кривую m в точках 1,2,3,4….Через середины полученных хорд проводим кривую ошибок ℓ, которая пересекаясь с данной кривой m, определяет точку касания К. Через данную точку касания К и данную точку А проводим искомую касательную.
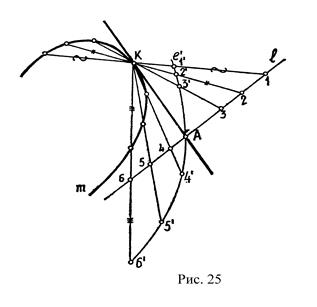
Чтобы построить касательную через точку К, взятую на кривой m, необходимо провести вспомогательную прямую ℓ расположенную приблизительно перпендикулярно к будущей касательной (рис.25). Затем через точку касания К проводим пучок секущих, пересекающих вспомогательную прямую ℓ в точках 1,2,3,4…. От этих точек откладываем соответствующие хорды. Через полученные на секущих точки: 1/, 2/, 3/,… проводим кривую ошибок ℓ/, которая пересекаясь со вспомогательной кривой ℓ, определяет вторую точку А, искомой касательной.

10.4. Определение длины отрезка кривой
Определение длины отрезка кривой находят приближенно. Для этого кривую линию заменяем на ломаную, вписанную в эту кривую с последующим определением натуральной величины каждого звена ломаной линии, тогда длина отрезка кривой линии определяется приближенно и равна сумме натуральных величин звеньев этой ломаной линии. Все отрезки звеньев ломаной линии размещаем параллельно П2 и на П2 определяем натуральную величину отрезка кривой линии (рис.26).

10.5. Цилиндрическая винтовая линия
Из пространственных кривых линий широко применяются в технике винтовые линии, которые являются направляющими поверхностей резьб, червяков, шнеков, пружин, сверл, разверток и т.д.
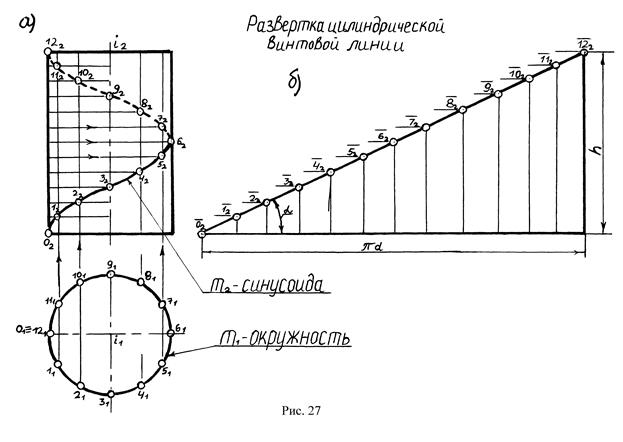
Цилиндрическая винтовая линия – пространственная кривая, полученная движением точки по образующей цилиндра, которая в свою очередь вращается вокруг его оси. На рис.27 показано образование винтовой линии, построение которой вытекает из способа ее образования движением точки по поверхности цилиндра. Для этого шаг винтовой линии, равный 60 мм делим на 4 части, затем каждую часть делим еще на 3 части, всего получается 12 делений. Основание цилиндра (окружность) делим тоже на 12 частей (см. рис.27а). Все остальное построение показано на рисунке 27.
Фронтальная проекция цилиндрической винтовой линии является синусоидой, а горизонтальная проекция - окружностью развертки цилиндрической винтовой линии – прямая линия, наклоненная к горизонтальной прямой под углом α. Угол α – угол наклона винтовой линии и может быть определен из выражения:
 (1)
(1)
10.6. Коническая винтовая линия
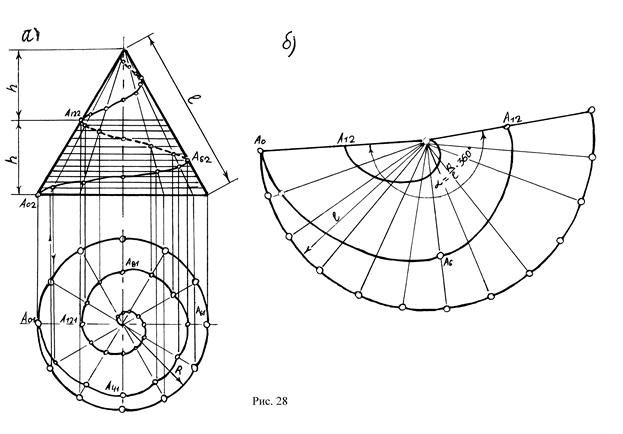
Конической винтовой линией – называется пространственная кривая, полученная равномерным движением точки по образующей конуса, которая равномерно вращается вокруг его оси. Для построения конической винтовой линии необходимо окружность основания конуса и шаг винтовой линии разделить на 12 частей, затем через точки деления основания провести соответствующие образующие конуса. Положение движущейся точки на каждой образующей конуса находим, исходя из того, что ее движение вдоль образующей пропорционально угловому перемещению этой образующей вокруг оси конуса (рис. 28б). Горизонтальная проекция конической винтовой линии - спираль Архимеда, фронтальная проекция – синусоида с затухающей амплитудой. Развертка конической винтовой линии является тоже спиралью Архимеда (рис. 28б).
 (2)
(2)
где ℓ– образующая конуса;
R - радиус основания.
11. Гранные и кривые поверхности
11.1. Общие сведения о поверхностях и их изображениях на комплексном чертеже. Точка и линия на поверхности
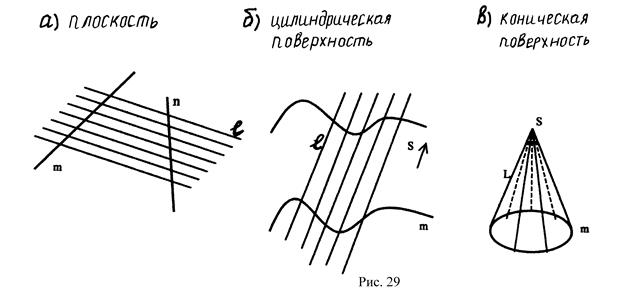
«Поверхность – это след линии, движущейся в пространстве» - это определение поверхности дал древнегреческий математик Эвклид, живший в III-IV веке до н. э. Движущаяся линия называется образующей. Она при своем движении может сохранять или изменять свою форму, подчиняясь какому-либо закону. Закон перемещения образующей включает другие линии, называемые – направляющими, по которым скользит образующая при своем перемещении в пространстве, а также характер движения образующей (рис.29).
В некоторых случаях одна из направляющих может превращаться в точку (рис. 29в) или находиться в бесконечности – цилиндрическая поверхность.
В начертательной геометрии поверхности рассматривают, исходя из кинематики их образования, и поверхность может быть определена как совокупность всех последовательных положений некоторой линии (образующей), перемещающейся в пространстве по определенному закону.
Сочетание образующих и направляющих поверхности называется ее каркасом. На комплексном чертеже любая поверхность задается своим определителем – совокупностью геометрических элементов задающих поверхность, позволяющих реализовать кинематический закон образования поверхности (см. рис. 29) и позволяющих построить каждую точку поверхности.
В зависимости от формы образующей и закона ее перемещения в пространстве, поверхности делят на две группы:
1. Линейчатые поверхности. Образующая – прямая линия.
В свою очередь они подразделяются:
 а) на развертываемые б) неразвертываемые
а) на развертываемые б) неразвертываемые
 | |||||
 | |||||
 | |||||
Гранные: Торсовые: С плоскостью Винтовые
Пирамида, конические, параллелизма: поверхности:
призма цилиндри цилиндроид, прямой и
ческие, коноид, косая наклонный
торсовые плоскость геликоид
2. Нелинейчатые поверхности. Образующая – окружность или кривая линия.
Подразделяются:
а) с постоянной образующей: б) с переменной образующей:
 | |||
 |
1. Поверхности вращения: 1. Циклические (каналовые)
тор, эллипсоид, параболоид, поверхности:
гиперболоид; поверхности труб перемен-
ного сечения;
2. Циклические поверхности: 2. Графические поверхности
трубчатые, пружины (земли, обуви, фюзеляжа
трубы изогнутые самолета).
Одна и та же поверхность может быть образована по разному (рис.30). Поверхность цилиндра, например, может быть образована:
1. Вращением образующей ℓ вокруг оси i.
2. Перемещением окружности к вдоль оси i.
3. Вращением вокруг оси i образующей m.

Если направляющей будет ломаная линия, состоящая из ряда прямолинейных звеньев, то поверхность цилиндра превращается в поверхность призмы, а поверхность конуса – в поверхность пирамиды.
11.2. Многогранники. Задание на комплексном чертеже Определение видимости элементов многогранников
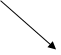
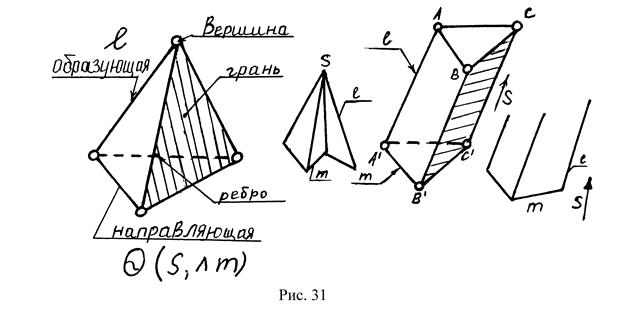
Поверхности, состоящие из ряда плоскостей – граней, называются многогранниками. Образуются перемещением образующей по ломаной линии направляющей. Наибольший практический интерес представляют пирамиды и призмы. Элементами многогранников являются вершины, ребра, грани (рис.31).
Совокупность всех ребер многогранника называется его сеткой или каркасом. Построение проекций многогранника сводится к построению проекций его сетки (каркаса).
Пирамида образуется перемещением образующей ℓ по ломаной направляющей m, при этом ℓ закреплена в точке S – вершине, которая неподвижна.
Призма образуется перемещением образующей ℓ по ломаной направляющей m, при этом ℓ остается параллельна заданному направлению S.
Задание на комплексном чертеже пирамиды и призмы представлено на рис.32 и рис.33.
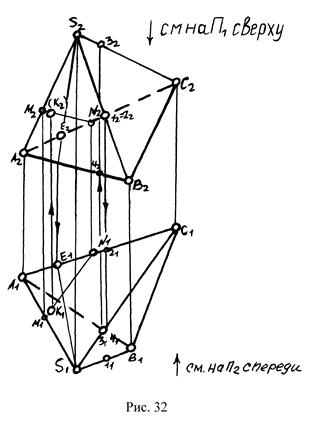

Видимость элементов многогранника определяется с помощью конкурирующих точек (см. рис. 32 и 33) и следующих правил:
1. Линии, образующие внешний контур (очерк) каждой проекции всегда видимы.
2. Если внутри очерка пересекаются проекции двух ребер, то одна из них видимая, а другая – нет. Видимость определяется при помощи конкурирующих точек.
3. Если проекция хотя бы одного из ребер, ограничивающих грань невидима, то невидима вся грань на этой плоскости проекции.
4. Если внутри очерка сходятся в одной точке проекции трех ребер, то или все три видимы, или все три не видны. Исходя из этого, достаточно определить видимость одной из трех проекций ребер, видимость двух других будет такой же.
5. Если видимость на одной проекции определена, видимость на другой проекции можно определить без дополнительных построений. Если последовательность наименований вершин при обходе какой –либо грани по часовой или против часовой стрелки одинакова на обеих проекциях, то и видимость грани на обеих проекциях также одинакова.
11.3. Поверхности вращения
Поверхности вращения имеют широкое применение в технике, так как являются определяющими многих деталей различных механизмов. Это объясняется распространенностью вращательного движения, простотой изготовления и обработки деталей с поверхностями вращения. Образуются вращением производящей линии вокруг неподвижной оси i, перпендикулярной одной из плоскостей проекций. Определителем поверхности вращения является образующая линия ℓ и ось вращения i (см. рис.34). При вращении образующей ℓ вокруг оси i перпендикулярной П1, т. А и т. Е описывают окружности, плоскости которых перпендикулярны оси i и следовательно параллельных между собой. Они называются параллелями и проецируются без искажения на ту плоскость, которая перпендикулярна оси i.

Параллель наименьшего диаметра называется горлом, наибольшего – экватором. Линия пересечения поверхностей ращения с плоскостью, проходящей через ось i, называется меридианом, а секущая плоскость называется меридиальной. Если секущая плоскость параллельна плоскости проекции П2, то она называется плоскостью главного меридиана. Эта плоскость определяет очерк поверхности на П2, разбивает поверхность на две части: переднюю – видимую на П2 и заднюю – не видимую на П2, что позволяет определить видимость элементов поверхности вращения при взгляде спереди. Совокупность меридианов или параллелей (или их сочетание) образует каркас поверхности вращения. Каждую точку поверхности можно построить с помощью линий каркаса. Наиболее удобными линиями при этом построении являются параллели.
11.4 Виды поверхностей вращения