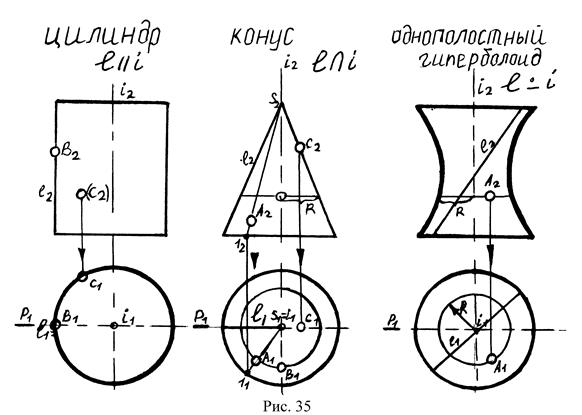
А. Поверхности, образованные вращением прямой линии вокруг оси i (цилиндр, конус, однополостный гиперболоид). Точки на поверхностях находят с помощью параллелей или образующих (см. рис.35). Определитель поверхностей один ∑(ί, ℓ).
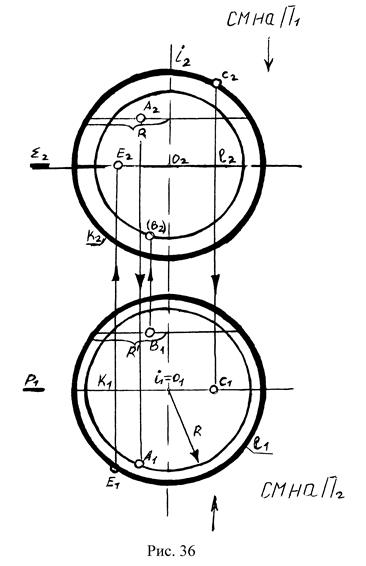
Б. Поверхности, образованные вращением окружности вокруг оси ί (сфера – шаровая поверхность, тор) (см. рис.36).
1. Шаровая поверхность – образующая окружность, вращается вокруг своего диаметра, так как ось вращения ί совпадает с ее диаметром. Экватор ℓ и меридиан к равны: ℓ = к (см. рис.36). Точка С лежит на главном меридиане.. Точка Е лежит на экваторе. Определить т. А, В можно с помощью параллелей своего радиуса R и R1.
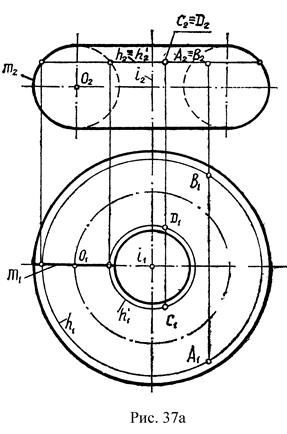
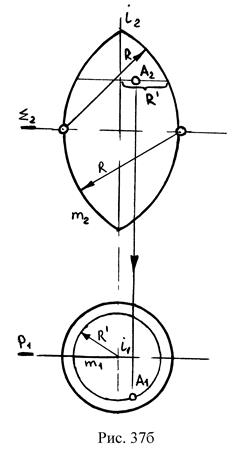
2. Тор - поверхность, образованная при вращении окружности вокруг оси ί принадлежащей плоскости этой окружности, не проходящей через ее центр.
Тор может быть открытым или закрытым в зависимости от R образующей окружности и центра, и расстояния от центра оси вращения (см. рис.37а, б).
В. Поверхности, образованные вращением кривых 2-го порядка (эллипс, парабола, гипербола) вокруг их оси (см. рис.38 а, б, в, г). Эти поверхности могут быть заданы уравнением 2-ой степени.
Рассмотрим поверхности, образованные вращением эллипса, параболы и гиперболы вокруг их осей.
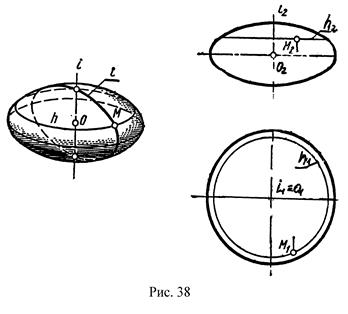
Эллипсоид вращения бывает двух видов:
а) вытянутый, который образуется при вращении эллипса вокруг его большой оси (рис.38);
б) сплюснутый, образованный вращением эллипса вокруг его малой оси.
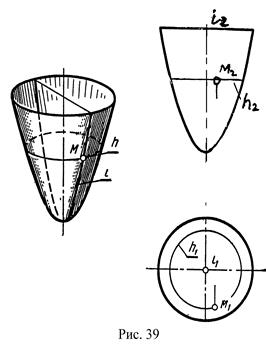
Параболоид вращения – поверхность, получающаяся вращением параболы вокруг ее оси (рис.39).
При вращении гиперболы могут получиться два вида гиперболоида вращения:
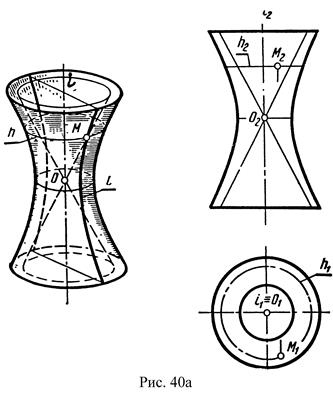
а) однополостный гиперболоид, образующийся при вращении гиперболы вокруг ее мнимой оси (рис. 40а). Однополостный гиперболоид является линейчатой поверхностью, так как может быть образован и вращением прямой ℓ(ℓ1, ℓ2) вокруг скрещивающейся с ней оси ί (ί1, ί2) (рис.41);
|
|
б) двуполостный гиперболоид образуется вращением гиперболы вокруг ее действительной оси (рис.40б).
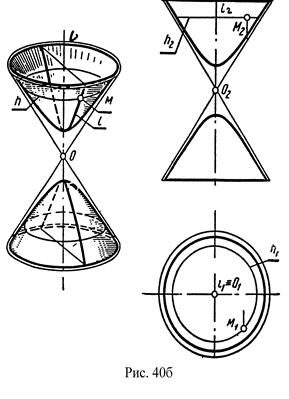

На рис.40 показан также асимптотический конус, который образуется при вращении асимптот гиперболы, причем, однополостный гиперболоид расположен во внешней области асимптотического конуса, а двуполостный гиперболоид – в его внутренней области.
Все рассматриваемые поверхности вращения, за исключением тора, являются алгебраическими поверхностями второго порядка, так как при пересечении прямой линии с каждой из этих поверхностей образуется не более двух точек. В результате пересечения прямой линии с поверхностью тора могут получиться четыре точки. Поэтому тор является поверхностью 4-го порядка.
Построение точки А на каждой из разобранных поверхностей вращения осуществлено с помощью соответствующей параллели (рис.35-41).
11.5. Циклические и топографические поверхности.
1. Циклической поверхностью называется поверхность, которая описывается какой-либо окружностью (образующей) постоянного или переменного радиуса при ее произвольном движении.
Из рассмотренных выше поверхностей к циклическим можно отнести все поверхности вращения, так как они могут быть образованы движением окружности (параллели), центр которой перемещается вдоль оси, а ее плоскость перпендикулярна к оси. К циклическим поверхностям можно также отнести те из поверхностей второго порядка, которые имеют круговые сечения.
|
|
Кроме этого, к циклическим поверхностям можно отнести каналовые и трубчатые поверхности (рис. 42).
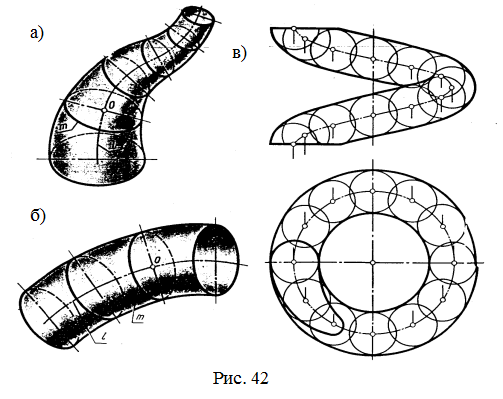
Каналовая поверхность образуется движением окружности переменного радиуса, причем центр окружности О перемещается по заданной кривой ℓ (направляющей), а ее плоскость остается перпендикулярной к этой кривой (рис. 42а).
Трубчая поверхность отличается от каналовой только тем, что ее образующая окружность m имеет постоянный радиус (рис. 42б).
Если направляющая ℓ трубчатой поверхности является цилиндрической винтовой линией, образуется трубчатая винтовая поверхность (рис.42в).
2. Топографической поверхностью называется поверхность, образование которой не подчинено какому-либо геометрическому закону.
К таким поверхностям относятся поверхности земной коры, корпуса судна, обшивки самолета, автомобиля и др.
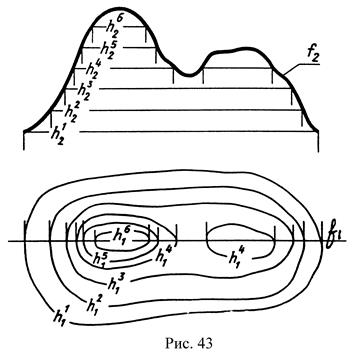
На чертеже эти поверхности изображают при помощи совокупности некоторых линий. Так, земная поверхность изображается при помощи семейства ее горизонталей (рис.43), поверхность обшивки самолета и другие – при помощи ее линий уровня (горизонталей, фронталей и профильных прямых) с последующей их увязкой и согласованием.
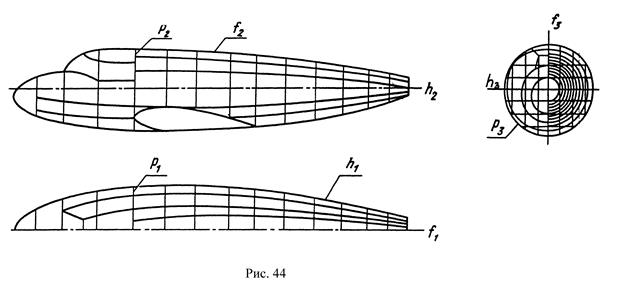
Такие поверхности часто называют каркасными, так как совокупность линий, которыми они задаются, образуют каркас поверхности. На рис.44 показан теоретический чертеж поверхности фюзеляжа самолета, который обычно выполняется в натуральную величину. На чертеже показаны три семейства линий рассматриваемой поверхности, а именно: горизонтали, фронтали, профильные прямые. При этом, чтобы не затемнять горизонтальную и фронтальную проекции, на чертеже не изображены фронтальные проекции горизонталей и горизонтальные проекции фронталей.
|
|
11.6. Линейчатые поверхности
Линейчатой называется поверхность, которая образована перемещением прямой линии (образующей) в пространстве по какому-либо закону. В зависимости от вида направляющих линий и характера движения образующей, получаются виды линейчатых поверхностей: развертываемые и неразвертываемые.
А. Развертываемые линейчатые поверхности (торс, цилиндрическая, коническая).
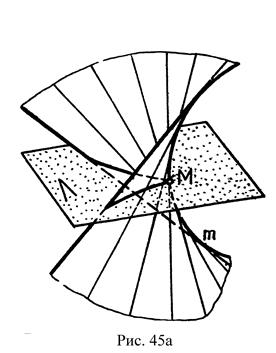
1. Торс - поверхность с ребром возврата m, образуется движением прямолинейной образующей ℓ, касающейся во всех положениях некоторой пространственной кривой m – ребро возврата, (рис. 45). Задается определителем Ø (l ~ m).
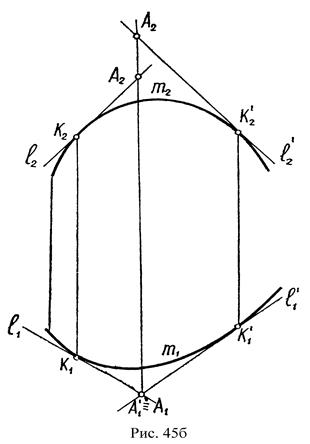
2. Цилиндрическая поверхность. Ребро возврата удалено в бесконечность. Поверхность образуется движением прямой ℓ, имеющей построенное направление S по некоторой кривой n (рис. 46). Определитель поверхности: ∑(S~n).
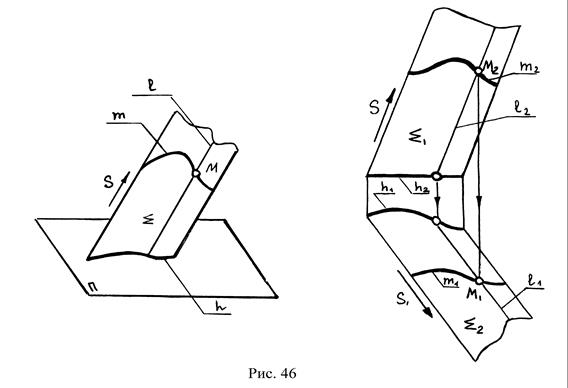
3. Коническая поверхность. Ребро возврата выродилось в точку S. Поверхность образуется перемещением прямой ℓ, проходящей через точку S, по некоторой кривой n, может иметь две полости (рис. 47). Определитель поверхности Δ(S~n).
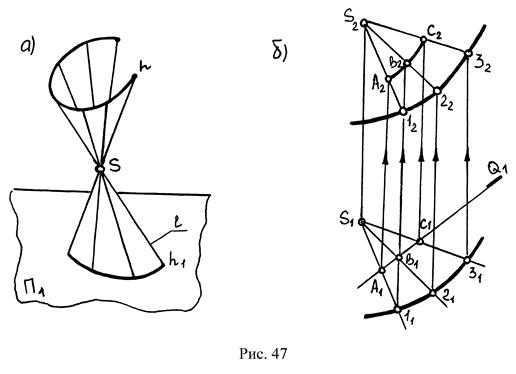
Б. Неразвертываемые линейчатые поверхности (цилиндроид, коноид, косая плоскость).
Этот вид поверхностей образуется перемещением прямой ℓ перемещающейся по двум направляющим и остающейся параллельной некоторой плоскости параллелизма, за которую обычно, принимают одну из плоскостей проекций П1 или П2.
1. Цилиндроид образуется перемещением прямой ℓ по двум направляющим и остающейся параллельно некоторой плоскости параллелизма (рис. 48а, б). Определитель поверхности Σ (~a, ~b) и Δ перпендикулярно П1.

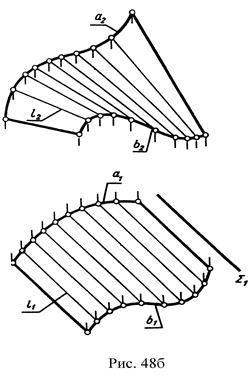
2. Коноид образуется перемещением прямолинейной образующей ℓ по двум направляющим: кривой и прямой, при этом ℓ остается параллельной некоторой плоскости параллелизма. Его определитель - Ø(b~a,∑) (рис. 49).
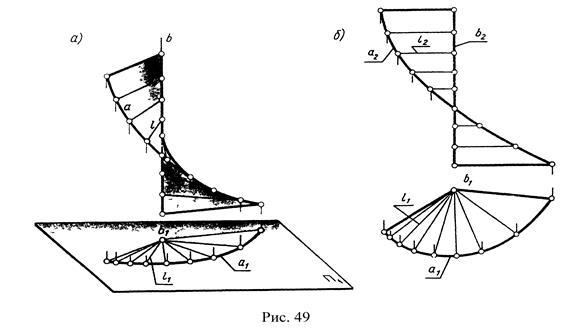
Если прямолинейная образующая n перпендикулярна к плоскости параллелизма, то коноид называется прямым, а если криволинейная направляющая m является цилиндрической винтовой линией, коноид называется винтовым геликоидом.
3. Косая плоскость (гиперболический параболоид) получается перемещением прямой ℓ по двум скрещивающимся прямым и остающейся параллельной некоторой плоскости параллелизма. Определитель поверхности
 |
Р(a \b, ∑), (рис. 50).
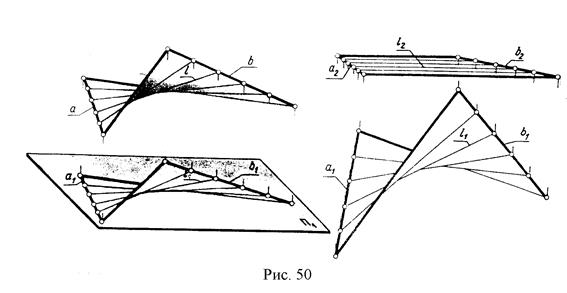
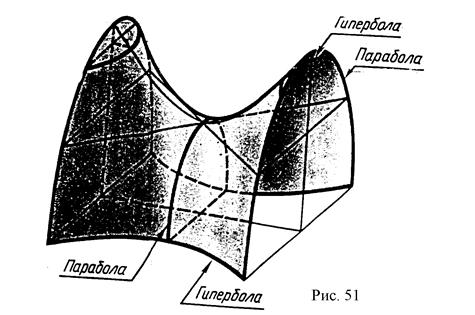
В сечении гиперболического параболоида могут получиться гиперболы, параболы, прямые линии (рис.51).
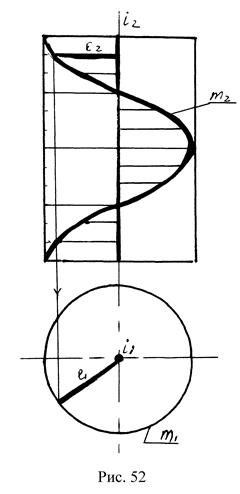
В. Линейчатые винтовые поверхности – геликоиды. Линейчатой винтовой поверхностью называется поверхность у которой одна направляющая – винтовая линия, а другая – прямая (ось винтовой линии). Определителями поверхности является винтовая линия и ее ось: Ø (ί, m, ℓ).
Геликоид называется прямым, если образующая прямая ℓ перпендикулярная к оси ί винтовой линии и эта ось ί выполняет роль прямой направляющей (рис. 52).
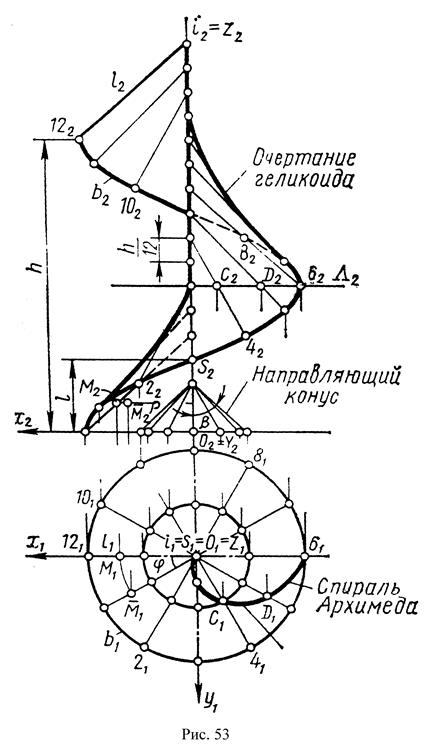
Если прямая образующая не перпендикулярна к оси ί, то геликоид называют косым или наклонным – Архимедов винт (рис. 53). Геликоиды могут быть закрытыми и открытыми. Прямая ℓ при пересечении оси ί винтовой линии, образует закрытый геликоид, если ℓ не пересекает ось ί, то образуется открытый геликоид. В процессе образования поверхности наклонного геликоида образующие располагаются параллельно образующим поверхности некоторого конуса вращения, ось ί которого совпадает с осью ί винтовой линии, а образующие имеют тот же наклон к оси ί винтовой линии, что и образующие геликоида. Этот конус называется направляющим. Отсюда определитель наклонного геликоида состоит из направляющих: винтовой линии m(m1, m2 , оси винтовой линии ί (ί 1, ί2) и образующей ℓ(ℓ1, ℓ2), которая располагается под углом α к оси винтовой линии. Наведя каркас из образующих ℓ и проведя огибающую семейства фронтальных проекций образующих ℓ, на П2 получаем очертание наклонного геликоида. Сечение геликоида плоскостью Σ (Σ2) перпендикулярной оси геликоида (нормальное сечение) представляет собой спираль Архимеда, требует специального построения (см. рис. 53).
12. Пересечение поверхностей с плоскостью и прямой линией.
При пересечении какой-либо поверхности плоскостью получается плоская фигура, которая называется сечением. Если секущая плоскость - проецирующая, то построение сечения проводится не сложно. Так как одна из проекций секущей плоскости вырождается в прямую линию, то на основании собирательного свойства проецирующих плоскостей эта проекция вбирает в себя все точки плоскости, в том числе и сечение. Таким образом, задача сводится к построению другой проекции сечения. Выделяются общие точки, которые принадлежат как плоскости, так и пересекаемой поверхности. Затем на основании принадлежности этих точек к фигуре строятся их недостающие проекции.
При пересечении плоскостью многогранника в сечении получается многоугольник (ограниченный замкнутой ломаной линией). Число его сторон и вершин равно числу граней и ребер многогранника, пересекаемых секущей плоскостью.
Построение сечения многогранника можно осуществить двумя способами:
1. Отыскание вершин многоугольника сечения - способ ребер. При этом построение сводится к тому, что несколько раз решается задача нахождении точки пересечения прямой (ребро) с плоскостью (секущая плоскость) –. первая позиционная задача
2. Отыскание сторон многоугольника сечения - способ граней. При этом несколько раз решается задача - нахождение линии пересечения двух плоскостей (грани и секущей плоскости) - вторая позиционная задача.
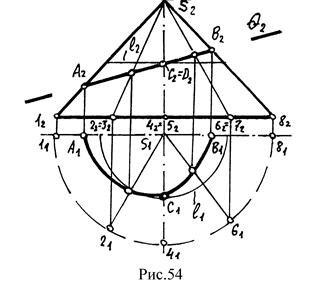
При пересечении плоскостью кривых поверхностей сечение получается плоскими кривыми линиями. Как уже было сказано, если секущая плоскость проецируется в прямую линию, то вторую можно построить по отдельным точкам (рис. 54).
Среди точек кривой пересечения имеются такие, которые особенно расположены по отношению к плоскостям проекций или занимают особые места на кривой. Такие точки называются опорными, и при построении сечения эти точки определяют в первую очередь. К опорным точкам относятся экстремальные точки, очерковые точки и точки смены видимости.
Экстремальные точки – это высшая и низшая точка сечения, самая близкая и дальняя относительно плоскости проекции П2, самая левая и самая правая относительно П3.
Очерковыми называются точки, проекции которых лежат на очерках поверхности.
Точки смены видимости разграничивают проекцию линии пересечения на видимую и невидимую часть. Точки смены видимости всегда выбираются из очерковых точек. Часто бывает так, что одна и та же точка является одновременно и экстремальной, и очерковой, и точкой смены видимости.
После определения опорных точек при построении кривой линии, для того чтобы точнее определить ее характер, определяется ряд случайных точек.
Случайные точки – это точки, которые взяты произвольно. Часто вид сечения заранее известен. Рассмотрим, какие сечения получаются в наиболее часто встречающихся поверхностях.
Конус – поверхность, в которой получается пять видов различных сечений:
1. Если секущая плоскость проходит через вершину конуса, то в сечении получается треугольник (все линии прямые). Если секущая плоскость не проходит через вершину, в сечении получаются кривые линии.
2. Если секущая плоскость расположена под непрямым углом к основанию и не параллельна ни одной из образующих, то в сечении получается эллипс (m).
3. Если секущая плоскость параллельна какой-либо одной образующей конуса, в сечении получается парабола (n).
4. Если секущая плоскость параллельна двум образующим, в сечении получается гипербола (k).
5. Если секущая плоскость параллельна основанию и в прямом конусе перпендикулярна оси, в сечении получается окружность (e), радиус окружности замеряется от оси до очерка (рис.55).
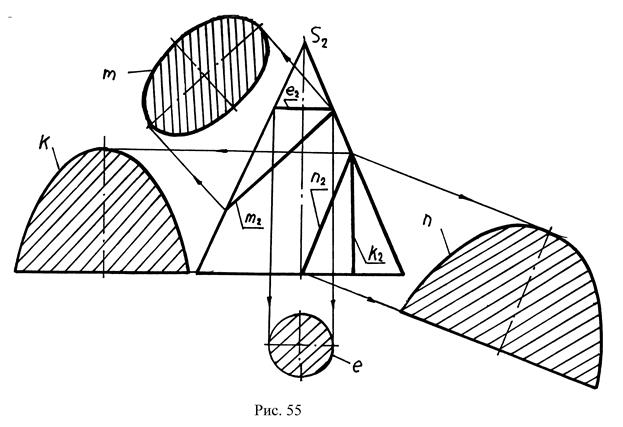
Цилиндр – поверность, в сечении которой получается три типа плоских фигур:
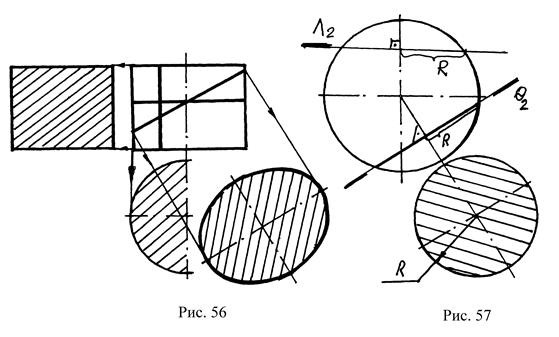
1. Если секущая плоскость расположена параллельно основанию и перпендикулярно оси, в сечении получается окружность, радиус окружности совпадает с радиусом основания.
2. Если секущая плоскость расположена параллельно оси, в сечении получается прямоугольник.
3. Если секущая плоскость расположена под углом к основанию и пересекает все образующие линии, в сечении получается эллипс (рис. 56).
Сфера – поверхность, в сечении которой всегда получается окружность, как бы ни располагалась секущая плоскость. Радиус окружности определяется следующим образом: из центра сферы на секущую плоскость опускается перпендикуляр, и радиус окружности замеряется от точки пересечения перпендикуляра с плоскостью до очерка сферы (рис.57) для q(q2), для L(L2) радиус берется от оси сферы до очерка.
Если секущая плоскость – общего положения, то для решения такой задачи удобно преобразовать комплексный чертеж так, чтобы секущая плоскость стала проецирующей, а затем продолжить решение по схеме, описанной выше (рис.58).
При пересечении поверхности с прямой линией необходимо определить две точки пересечения, которые называются точками входа и выхода прямой.
Задача решается по следующей схеме:
1. Одна из проекций прямой заключается в проецирующую плоскость, затем решается задача построения сечения поверхности проецирующей плоскостью. После того как построено сечение, находятся общие точки сечения с проекцией прямой.
2. Недостающие проекции точек пересечения строятся на основании принадлежности их к прямой при помощи линий связи.
3. Определяется видимость (без определения видимости задача считается нерешенной) (рис. 59).
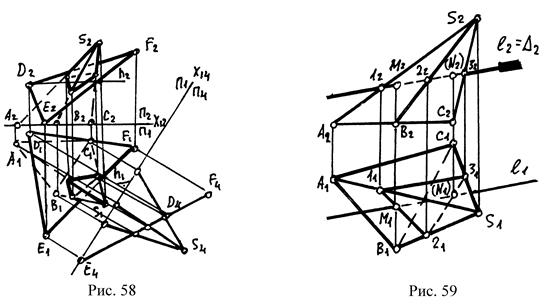
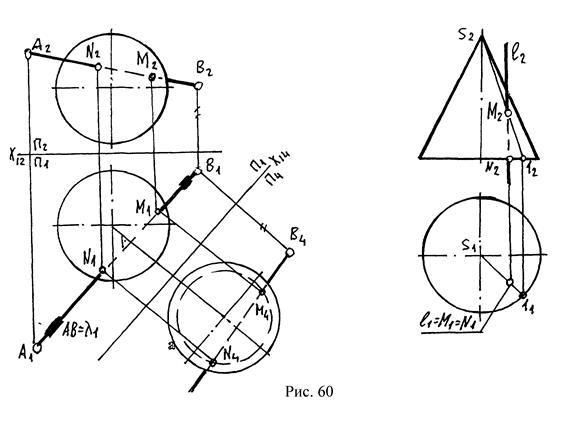
При решении задачи на пересечение прямой линии с поверхностью могут быть широко использованы способы преобразования комплексного чертежа, в частности, способ замены плоскостей (рис.60).
13. Взаимное пересечение двух поверхностей.
При взаимном пересечении двух поверхностей образуется одна или две замкнутые пространственные линии (линии перехода), которые принадлежат одновременно каждой из пересекающихся поверхностей. Построение этих линий производится по отдельным точкам. Одна линия получается в случае врезки, т.е. когда обе поверхности участвуют в пересечении частично. Две линии получаются в случаи проницания, т.е. когда хотя бы одна из поверхностей полностью участвует в пересечении.
Если в пересечении участвуют два многогранника, то линия пересечения получается ломаная, состоящая из ряда прямолинейных отрезков. Если пересекаются многогранник с кривой поверхностью, то линия пересечения - ломаная кривая. Если пересекаются две кривые поверхности, результат - плавная кривая линия. Существует последовательность определения точек линии пересечения. В первую очередь определяются опорные точки. К ним относятся экстремальные, очерковые (определяются на каждом очерке каждой поверхности), точки смены видимости (выбираются среди очерковых). Если в пересечении участвует многогранник, то точки пересечения его ребер с другой поверхностью также относятся к опорным точкам.
После того, как найдены опорные точки, определяются случайные точки. Такие точки нужны, если в пересечении участвует кривая поверхность, так как если хотя бы одна из поверхностей кривая, то в результате получается кривая линия. Кривая линия строится тем точнее, чем больше взято случайных точек.
Задачи на взаимное пересечение двух поверхностей делятся на три группы сложности:
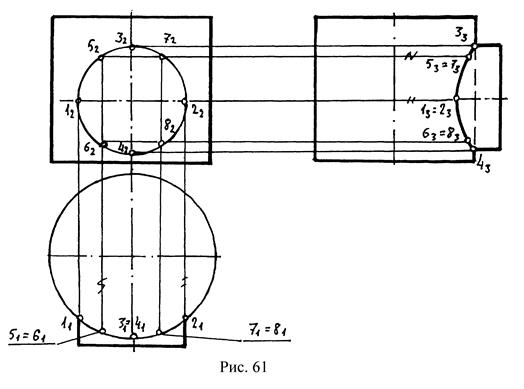
Первая группа сложности – обе поверхности проецирующие. В этом случае две проекции общего элемента (т.е. линии пересечения) заданы на исходном комплексном чертеже – они совпадают с главными (вырожденными) проекциями проецирующих поверхностей. Требуется их только обозначить. Иногда возникает необходимость построить третью недостающую проекцию. В этом случае одну из заданных проекций линий пересечения разбивают на точки, на второй проекции заданной линии находятся проекции обозначенных точек, и затем по двум проекциям точек при помощи линий связи строится третья проекция (рис.61).
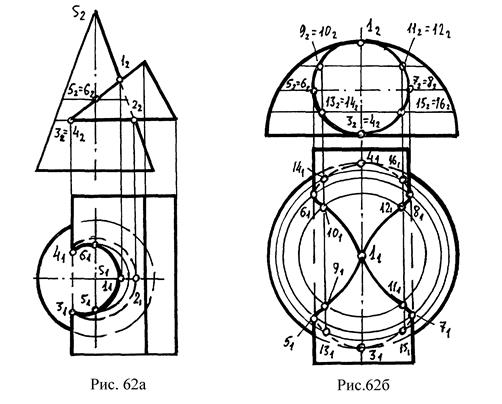
Вторая группа сложности – одна поверхность проецирующая, другая общего положения. Одна проекция общего элемента задана на исходном чертеже – она совпадает с главной (вырожденной) проекцией проецирующей поверхности. Требуется её обозначить. Вторая проекция общего элемента определяется из условия его принадлежности к поверхности общего положения. Для этого необходимо разбить имеющуюся проекцию линии пересечения на точки (опорные и случайные), а затем строить недостающие проекции этих точек из условия принадлежности их поверхности общего положения. Если конус - поверхность общего положения (рис.62а), а призма – проецирующая поверхность, то фронтальная проекция линии пересечения, совпадающая с фронтальной проекцией призмы разбивается на точки и через них проводят параллели. Затем измеряют радиус параллели (от оси до очерка) и на другой проекции проводят окружность этого радиуса, после чего при помощи линий связи находятся недостающие проекции точек линии пересечения. Когда найдены все точки, их соединяют плавной кривой.
Так же решается задача, если фигурой общего положения является сфера (рис.62б).
Третья группа сложности – обе пересекающиеся поверхности общего положения. В этом случае ни одна из проекций линии пересечения поверхностей на исходном комплексном чертеже не задана. Такие задачи решаются способом введения посредников, что сводит решение каждой задачи к пересечению двух линий, полученных от пересечения посредника с заданными поверхностями.
Существует два способа решения такого типа задач: способ вспомогательных секущих плоскостей и способ сфер.
1. Способ вспомогательных секущих плоскостей применяется в том случае, если в сечении обоих поверхностей получаются простые по графическому построению линии (окружности или прямые). Секущие плоскости задаются обязательно частного положения, в большинстве случаев выбираются как посредники плоскости уровня. Рассмотрим этот способ решения задачи на примере.
Пример:
Построить линию пересечения полусферы Р и пирамиды Q (рис.63).
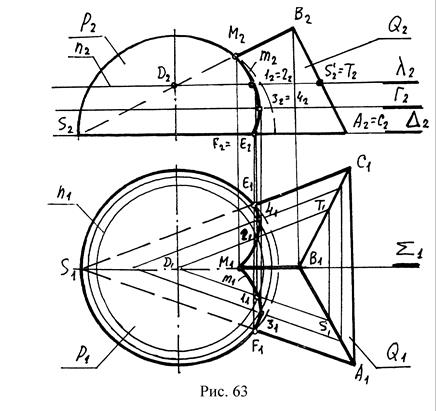
а) Анализ чертежа показывает, что это задача третьей группы сложности (пирамида и полусфера - фигуры общего положения). Задача решается при помощи посредников. За посредники выбираем горизонтальные плоскости уровня. Они пересекают Р по параллелям, а Q по треугольникам – графически простым линиям.
б) Определяем опорные точки на линии пересечения m. Находим точки пересечения ребер пирамиды с полусферой: M1, F1 и Е1. Точку М=SBÇP находим с помощью плоскости S(S1) – плоскости главного меридиана полусферы Р. Точки Е и F получаются в результате пересечения ребер AS и SC и полусферой Р, найдены точки с помощью плоскости D(D2) – плоскость экватора полусферы. Точки М, Е, F являются экстремальными точками, а так же очерковыми на П2, точки Е и F очерковыми на П1, и они же точки смены видимости на П1.
в) Случайные точки определяем с помощью плоскостей уровня l(l2) и Г(Г2); lÇP=n(n2,n1) - параллель полусферы lÇQ= l (l 2, l 1) – треугольник DTS; nÇL=точки 1 и 2. Аналогично с помощью плоскости Г(Г2) находятся точки 3 и 4.
г) Соединяем найденные точки линии m с учетом видимости.
д) Определяем взаимную видимость Р и Q.
2. Способ вспомогательных сфер основан на одном свойстве поверхности вращения: если центр сферической поверхности расположен на оси поверхности вращения (сфера и поверхность вращения в этом случае называются соосными), то при их взаимном пресечении образуется окружность. Причем, плоскости этих окружностей располагаются перпендикулярно к оси поверхности вращения (рис.64а, б).
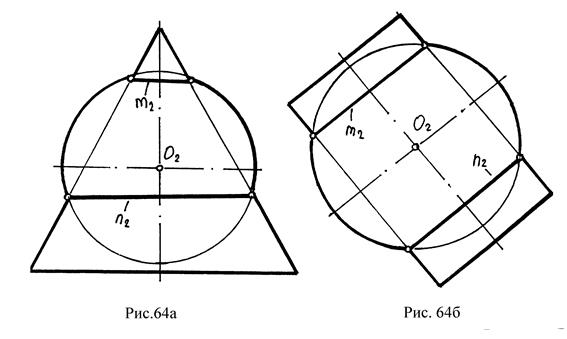
Благодаря этому свойству, сферические поверхности используются в качестве вспомогательных при определении точек линии пересечения между поверхностями двух тел вращения с пересекающимися осями. Способ, где посредником берется сфера, называется способом вспомогательных концентрических сфер. Применяется он, только если соблюдаются три условия:
1. Обе поверхности должны быть поверхностями вращения.
2. Обе поверхности должны иметь общую ось симметрии (т.е. должны быть соосными).
3. Оси симметрии пересекающихся поверхностей должны быть прямыми линиями, и эти оси должны пересекаться.
Рассмотри применение этого способа на практическом примере.
Пример:
Построить линию пересечения между поверхностями цилиндра и конуса, оси которых пересекаются под углом (рис.65). Общая плоскость симметрии обоих тел Р(Р1) расположена параллельна плоскости П2.
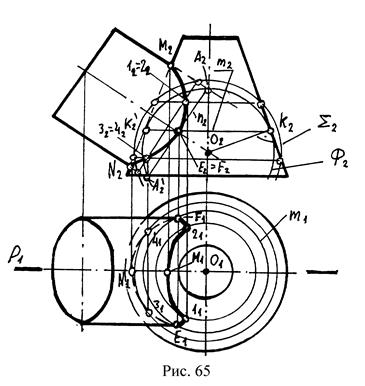
Поэтому высшая и низшая точки линии пересечения М(М1, М2) и N(N1, N2) получаются в пересечении очерковых образующих. Все остальные точки линии пересечения находим с помощью вспомогательных сфер, проводим из точки пересечения осей конуса и цилиндра О(О1, О2). Сферой наименьшего радиуса является сфера, вписанная в поверхность одного из пересекающихся тел. С поверхностью другого тела такая сфера должна пересекаться. Для того чтобы определить, в какую из пересекающихся фигур вписывается наименьшая сфера и точки пересечения осей О(О2) на очерковые образующие фигуры опускаем перпендикуляры; тот из перпендикуляров, который окажется больше, и будет являться радиусом наименьшей сферы (Rmin=O2K2). Проведенная из центра О(О2) вписанная в поверхность конуса сфера Ф(Ф2) касается поверхности конуса по окружности m(m2,m1) и пересекается с поверхностью цилиндра по окружности n(n2). Обе эти окружности на П2 проецируются в виде прямых отрезков К2К`2 и A2A`2. Так как построенные окружности принадлежат одной и той же сфере Ф, то они пересекаются в двух точках Е(Е1, Е2) и F(F1, F2), которые являются общими для поверхностей конуса и цилиндра, и, следовательно, располагаются на линии их пересечения.
Произвольные точки 1, 2, 3, 4 определены с помощью концентрической сферы S(S2) радиусом произвольно несколько большим, чем радиус вписанной сферы. После того как все точки найдены в двух проекциях они соединяются плавной линией на П2, и на П1 с учетом видимости.
Если две пересекающиеся поверхности являются фигурами вращения и имеют общую плоскость симметрии, но оси этих плоскостей не пересекаются, то в этом случае применяется способ эксцентрических сфер. При этом способе точки линии пересечения между двумя поверхностями определяются при помощи сфер, проводимых из различных центров.
Разберем применение этого способа на примере.
Пример:
Построить линию пересечения между поверхностями конуса и тора (рис.66).
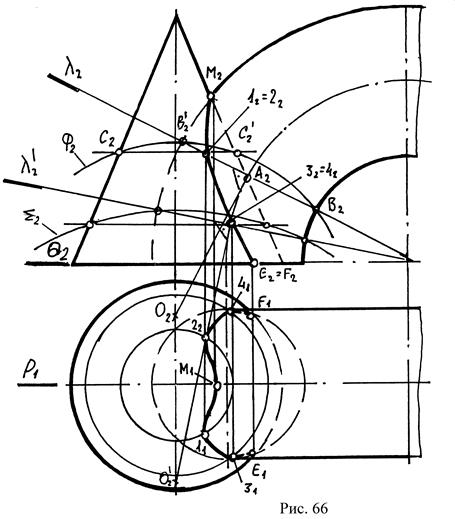
Сначала определяем опорные точки. Общая плоскость симметрии обоих тел расположена параллельно плоскости П2. Поэтому высшая точка линии пересечения М(М1, М2) получается в пересечении очерковых образующих. Плоскость основания обоих фигур также совпадает и параллельна П1. На П1 оба основания проецируются от проведения плоскости q(q2) в виде окружностей и их пересечения дают две нижних точки линии пересечения Е(Е1, Е2) и F(F1, F2). Для определения произвольных точек 1, 2 проводят через ось тора вспомогательную фронтально проецирующую плоскость, которая пересечет тор по окружности с центром А(А2) эта окружность проецируется на П2 в виде отрезка В2В`2. из центра этой окружности (А2) проводится перпендикуляр к отрезку В2В`2. Пересекаясь с осью конуса, он определяет центр сферы О(О2). Из центра О(О2) проводится вспомогательная сфера Ф(Ф2) такого радиуса, чтобы она пересекала тор по окружности ВВ`(В2В`2). Эта сфера пересекает конус по окружности СС`(C2C`2). Обе найденные окружности пересекутся в двух точках 1(12,11) и 2(22,21), располагающихся на линии пересечения поверхностей конуса и тора.
Точки 3 и 4 определены при помощи вспомогательной сферы S(S2) из центра O`(O`2), найденного аналогичным построением с помощью вспомогательной плоскости Q(Q2). После того как все точки найдены, в двух проекциях они соединяются плавной кривой линией на П2 и на П1. В заключение определяется взаимная видимость конуса и тора.
В некоторых случаях кривая, которая получается при пересечении поверхностей вращения, распадается на две плоские кривые, т.е. на кривые второго порядка. Условия, при которых происходит распадение линии пересечения на две плоские кривые, оговариваются в трех теоремах:
Теорема 1. Если две поверхности вращения (второго порядка) пересекаются по одной плоской кривой, то они пересекаются и еще по одной плоской кривой (рис. 67а, б).
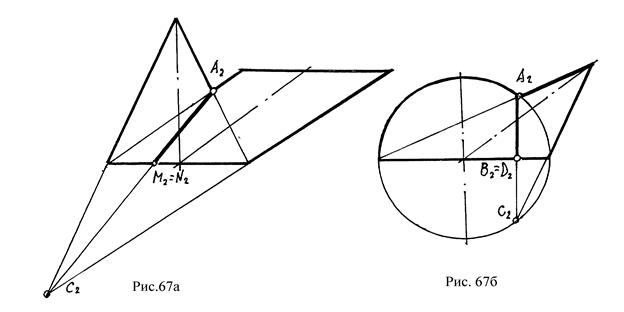
Теорема 2. Если две поверхности вращения касаются в двух точках (рис. 68 N и М), то линия их пересечения распадается на две плоские кривые. Плоскости этих кривых пересекаются по прямой (рис. 68 MN), соединяющей точки касания поверхностей.
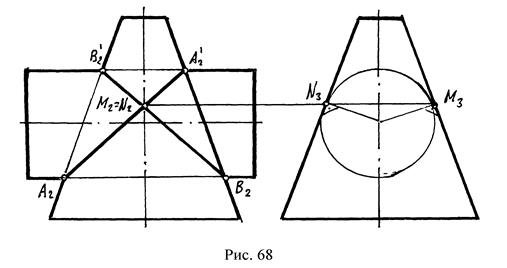
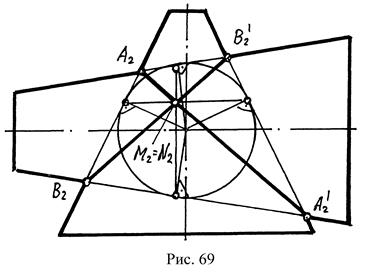
Теорема 3. (теорема Г. Монжа) Если поверхности вращения второго порядка вписаны или описаны около третьей поверхности вращения второго порядка (сферы), то в результате их пересечения образуется две плоские кривые второго порядка (рис.69).
14. Развертки поверхностей.
Разверткой называют плоскую фигуру, полученную при совмещении развертываемой поверхности с плоскостью.
Поверхности, которые можно совместить с плоскостью без разрывов и складок, называют развертывающимися.
Рассмотрим различные виды разверток:
а) Точные развертки (гранные поверхности, конус и цилиндр) (рис. 70).
б) Приближенные (кривые развертываемые поверхности). Кривую поверхность заменяют гранной поверхностью. Точность развертки зависит от величины отсеков гранной поверхности, а значит от их количества (рис.71). Чтобы из приближенной развертки получить нужную поверхность, достаточно изогнуть тонкий лист на котором начерчена развертка.
в) Приближенно – условные развертки (не развертываемые кривые поверхности).
Теоретически у не развертываемых поверхностей разверток быть не может. Развертка получается условно, если эту поверхность заменить такими простыми развертывающимися поверхностями, как цилиндры и конусы. Последние в свою очередь заменяют многогранными поверхностями, которые и развертывают.
Существует несколько способов построения разверток поверхностей:
1. Способ треугольника (триангуляция). Этот способ применяется для построения разверток гранных поверхностей и всех линейчатых поверхностей. Кривую линейчатую поверхность заменяют вписанной гранной поверхностью (рис.70, 71).
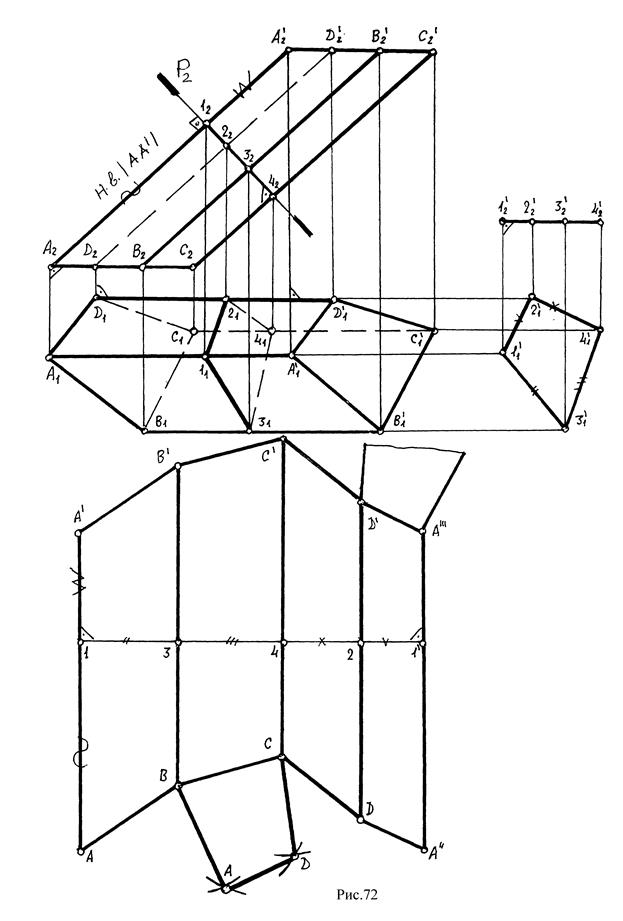
2. Способ нормального сечения (рис.72).
3. Способ раскатки.
4. Способ вспомогательных цилиндров и конусов (для построения условно – приближенных разверток).
Рассмотрим несколько примеров построения разверток поверхностей:
Пример 1. Построить развертку поверхности пирамиды (рис. 70). Поскольку у пирамиды боковые грани являются треугольниками, то построение её развертки сводится к построению натуральных величин этих треугольников и натуральных величин основания. Натуральные величины ребер определены способом плоскопараллельного перемещения. Развертка пирамиды – это ряд пристроенных друг к другу граней и основания.
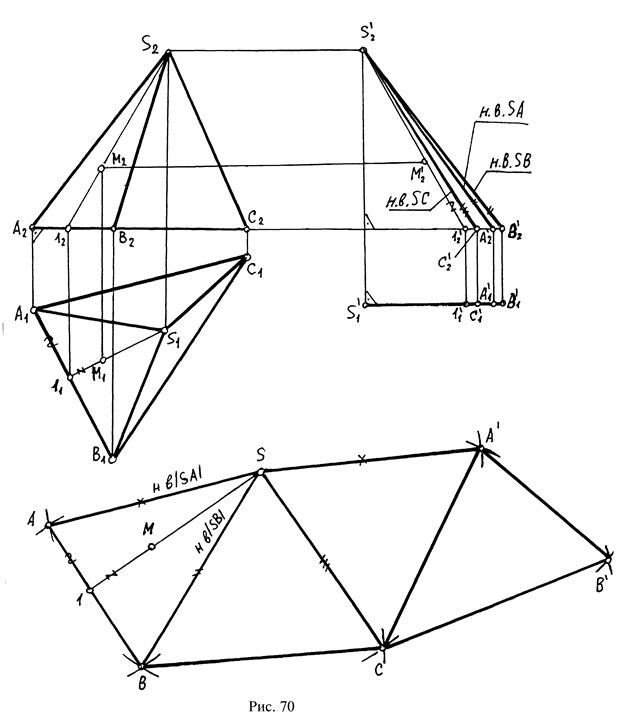
Пример 2. Построить развертку боковой поверхности усеченного конуса (рис. 71). Заменяем поверхность конуса восьмиугольной пирамидой, вписанной в конус. Натуральную величину образующих определяем способом плоскопараллельного перемещения.
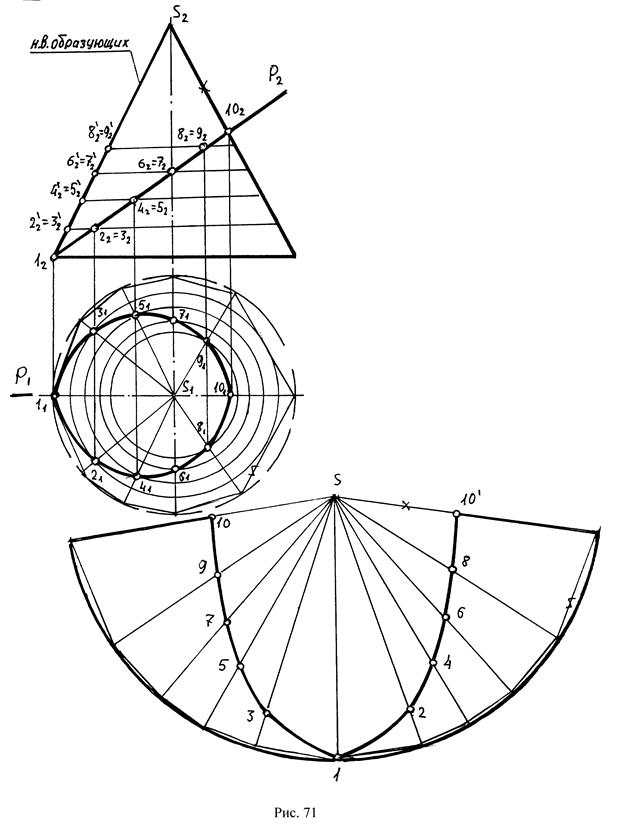
Это построение можно выполнить на исходном чертеже, переместив все образующие и отрезки на них в положение крайней образующей, которая расположена параллельна П2. Дуги основания конуса заменяем рядом хорд и развертку строим аналогично развертке пирамиды (ряд треугольников). Затем полученные точки соединяем плавной кривой линией.
Пример 3. Построить развертку наклонной призмы (рис. 72). Для определения расстояния между ребрами призмы нужно построить натуральную величину нормального сечения плоскостью Р(Р2), перпендикулярной к боковым ребрам. Натуральную величину нормального сечения определяют заменой плоскостей проекции или плоскопараллельным перемещением. На развертке фигура нормального сечения представляет собой прямую линию, длина которой равна сумме сторон сечения. Натуральные величины ребер AA`, BB`, CC`, ДД` снимают с П2, т.к. ребра данной призмы параллельны П2, то и натуральная величина их читается на П2. Если ребра призмы – прямые общего положения, то необходимо сначала определить их натуральную величину, затем натуру нормального сечения и строить развертку по описанной выше рекомендации.