Цель работы: изучение работы клеедощатой балки.
Задачи: определить нагрузку на балку и сравнить ее с расчетной, определить модуль упругости клееной древесины, определить величины и характер распределения нормальных напряжений по высоте поперечного сечения балки, построить теоретический и экспериментальный графики прогибов балки. Определить расчетную нагрузку РТ, при которой клееная балка достигает предельного состояния, и произвести подсчет прогиба балки при условной нормативной нагрузке

(где 1,2 – условный коэффициент надежности по нагрузке); выявить
зависимость прогиба f балки от нагрузки Р и подсчитать фактическую
величину модуля упругости древесины балки; установить характер
распределения нормальных напряжений по высоте поперечного сечения
балки и сравнить его с теоретическим; определить разрушающую нагрузку
Р разр. для балки и подсчитать коэффициент безопасности по формуле

1.Установление фактических размеров образца
 |
Рис. 1. Клеедощатая балка прямоугольного поперечного сечения.
Исходные данные: l = 1950 мм;h = 158 мм;b = 50 мм.
2. Схема нагружения образца и расстановка приборов
 |
Рис. 2. Схема загружения балки и расстановки приборов:
1– клеедощатая балка; 2– неподвижная опора; 3– подвижная опора; 4–распределительная траверса; 5– стальной валик; 6– металлическая накладка; 7– нагруженная траверса.
3.Определение расчетной нагрузки на балку
Расчетная нагрузка Р определяется исходя из расчетной несущей
способности балки или достижения ею предельного прогиба.
а) из условия обеспечения прочности от действия нормальных напряжений

где:  kH×м – расчетный изгибающий момент, Н
kH×м – расчетный изгибающий момент, Н  м (кгс
м (кгс  см)
см)

 – момент сопротивления поперечного сечения;
– момент сопротивления поперечного сечения;
 – расчетное сопротивление древесины изгибу, МПа (
– расчетное сопротивление древесины изгибу, МПа ( ) (
) ( =13 МПа)
=13 МПа)

б) из условия обеспечения прочности клеевого шва от действия касательных напряжений
 , где
, где 
где: Q = P / 2=13.27/2=6.64, Н (кгс);
Sбр = b×h2 / 8=0.05×0.1582 /8=156.03 см3;
Jбр = b×h3 / 12=5×15,83/12=1643,46 см4;
bрасч = b×K – при расчете на скалывание по клеевому шву, где К=0.6 – коэффициент непроклея, принимаемый по действующим нормам.
После подстановки получим:
bрасч = b×K=0.6×5=3 см
Rck=2.1 MПА

в) из условия достижения предельного прогиба


где Pn =Р/n;(n=1.2 – усредненный коэф. надежности);
Е =104 МПа– модуль упругости древесины..
После преобразования получаем:

где 



ИСПЫТАНИЕ БАЛКИ
| Этап нагружения | Нагрузки P, кН | Прогибомеры | Средняя величина приращения отсчётов
 ср= ср= 
| Разность приращения отсчётов
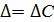 2- 2-  ср ср
| Полный прогиб балки
 п п
| |||||
| П-1 | П-2 | П-3 | ||||||||
| Отчет C1 | Разность отсчетов  С1 С1
| Отсчёт С2 | Разность
отсчётов  С2 С2
| Отсчёт С3 | Разность
отсчётов  С3 С3
| |||||


| Этап нагружения | Нагрузка Р, кН | Тензодатчики | |||||||||
| Т-1 | Т-2 | Т-3 | Т-4 | Т-5 | |||||||
| Отсчет С1 | Разность
Отсчетов  С1 С1
| Отсчет С2 | Разность
Отсчётов  С2 С2
| Отсчет С3 | Разность
Отсчётов  С3 С3
| Отсчет С4 | Разность
Отсчётов  С4 С4
| Отсчет С5 | Разность
Отсчётов  С5 С5
| ||

Прибор: АИД – 2М с компенсирующим устройством с выходом шкалы С*10-5
ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЯ








sт=13Mпа sэкс=14,4Мпа
 sт=13 sэкс=12,49
sт=13 sэкс=12,49
Рис. 3. Эпюра напряжений по высоте сечения балки: