Закон сохранений момента импульса

Момент силы относительно неподвижной оси Z

Скалярная величина М, равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z (см, рисунок).

Значение момента М. не зависит от выбора положения точки О на оси z. Если ось z совпадает с направлением вектора М, то момент силы представляется в виде вектора, совпадающего с осью:

 

 

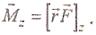
Кинетическая энергия вращения

Абсолютно твердое тело вращается вокруг неподвижной оси z. Разбивая тело на элементарные объемы массами m ₁, m ₂,..., m_п, находящиеся от оси на расстояниях г₁, г₂,..., г_n, запишем

 

Поскольку ω = v_l/r₁=v₂/r₂=:...= v_n/r_n,

 

где J_z — момент инерции тела относительно оси z. Из сравнения формул

 

 

следует, что момент инерции — мера инертности тела при вращательном движении.

Уравнение динамики вращательного движения твердого тела

Работа вращения тела идет на увеличение его кинетической энергии:

 

(М _z — момент сил относительно оси z),

 

 

Тогда

или

 

Учитывая, что ω = получаем

 

— уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Если ось вращения совпадает с главной осью инерции, проходящей через

центр масс, то имеет место векторное равенство

где J -главный момент инерции тела (момент инерции относительно главной оси).

Момент импульса относительно неподвижной точки О

Физическая величина, определяемая векторным произведением

 

где r — радиус-вектор, проведенный из точки О в точку А; -импульс материальной точки; L -псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от г к р.

Момент импульса относительно неподвижной оси

Это скалярная величина L, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса L. не зависит от положения точки О на оси z.

Закон сохранений момента импульса

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц. Учитывая, что

получим

Продифференцируем уравнение по времени:

 

 

Можно показать, что имеет место век­торное равенство

 

 

Это выражение — еще одна форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси. В замкнутой системе момент внешних сил М = 0 и 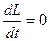, откуда

 

— закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени. Это — фундаментальный закон природы. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.

4. Гироскопы

Гироскопом называют массивное симметричное тело, враща­ющееся с большой угловой скоростью вокруг своей оси симмет­рии. Рассмотрим поведение гироскопа на примере волчка. Опыт показывает, что если ось вращающегося волчка наклоне­на к вертикали, то волчок не падает, а совершает так называе­мое прецессионное движение (прецессию) — его ось описывает конус вокруг вертикали с некоторой угловой скоростью ω ', причем оказывается: чем больше угловая скорость ω вращения волчка, тем меньше угловая скорость прецессии ω '. Такое поведение волчка-гироскопа можно объяснить с помощью уравнения моментов, если только принять, что ω » ω ' (это условие, кстати, поясняет, что имеется в виду под бо­льшой угловой скоростью гироскопа).

Момент импульса L прецессирующего волчка относительно точки опо­ры O можно представить в виде суммы момента им­пульса L _ω, обусловленного вращением волчка вокруг своей оси, и некоторого добавочного момента импульса L ', вызванно­го прецессией волчка вокруг вертикальной оси,

т. е. L= L _ω + L '

 

Поскольку ось волчка совпадает с одной из его главных осей, то L _ω = I ω, где I — момент инерции вол­чка относительно этой оси. Кроме того, ясно, что чем меньше угловая скорость прецессии, тем меньше и соответствующий момент L '. При ω » ω' во всех практически интересных случаях L _ω » L ', поэтому результирующий момент импульса L почти совпадает с L _ω как по модулю, так и по направлению, — мож­но считать, что

L = I ω

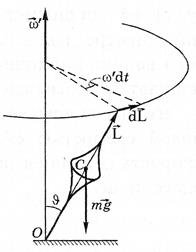
Зная поведение вектора L, мы найдем и характер движения оси волчка-гироскопа.Mомент импульса L относительно точки О (рис.) получает за время dt приращение d L = M dt,совпадающее по направлению с вектором
M- моментом внешних сил относительно той же точки О (в данном случае это мо­мент силы тяжести mg). Из рисунка вид­но, что dL L. В результате вектор L, (а,следовательно, и ось волчка) будет пово­рачиваться вместе с вектором M вокруг вертикали, описывая круговой конус с уг­лом полураствора . Волчок-гироскоп бу­дет прецессировать вокруг вертикальной оси с некоторой угловой скоростью ω '.

Найдем связь между векторами M, L и ω '. Согласно рисун­ку, модуль приращения вектора L за время dt есть = Lsin ·ω'.dt или в векторном виде dL = dt После подстановки этого выражения в d L = M dt получим

= M

Из этого уравнения видно, что момент силы M определяет угловую скорость прецессии ω ' (а не ускорение!). Поэтому мгновенное устранение момента M приводит к мгновенному ис­чезновению и прецессии. В этом отношении можно сказать, что прецессия не обладает инерцией.

Заметим, что момент сил M, действующий на гироскоп, мо­жет иметь любую природу. Для обеспечения регулярной пре­цессии (постоянной угловой скорости ω') важно только, чтобы вектор M, не меняясь по модулю, поворачивался вместе с осью гироскопа.

Пример. Найдем угловую скорость прецессии наклонного волчка мас­сы m, вращающегося с большой угловой скоростью ω вокруг своей оси симметрии, относительно которой момент инерции волчка равен I. Центр масс волчка находится на расстоянии l от точки опоры.

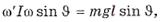Согласно = M, где 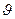— угол между

вертикалью и осью волчка (рисунок). Отсюда

 

Величина ω ' не зависит от угла наклона 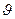оси волчка. Кроме того, полученный результат показывает, что ω ' обратно пропорциональна ω, т. е., действительно, чем больше угловая скорость волчка, тем меньше угловая скорость его прецессии.

Гироскопический момент. Рассмот­рим эффект, возникающий при вынуж­денном вращении оси гироскопа. Пусть, например, ось гироскопа укреплена в U-образной подставке, которую мы бу­дем поворачивать вокруг оси 00'.

Если момент импульса L гироскопа направлен вправо, то при таком пово­роте за время dt вектор L получит приращение dL — вектор,направленный за плоскость рисунка.Это озна­чает, что на гироскоп действует момент сил М, совпадающий по направлению с вектором dL. Момент M обусловлен возникнове­нием пары сил F, действующих на ось гироскопа со стороны подставки. Ось же гироскопа в соответствии с третьим законом Ньютона будет действовать на подставку с силами F '). Эти силы называют гироскопическими; они создают гироскопи­ческий момент M ' = - M. Заметим, что в данном случае гиро­скоп не обладает способностью противодействовать изменению направления его оси вращения.

Появление гироскопических сил называют гироскопическим эффектом. Подобный гироскопический эффект, связанный с возникновением гироскопического давления на подшипники, наблюдается, например, у роторов турбин на кораблях при по­воротах и качке, у винтовых самолетов при виражах и т. п.

Проследим действие гироско­пического момента на примере ги­роскопа, ось которого вместе с рамкой может свобод­но поворачиваться вокруг гори­зонтальной оси 00' U-образной подставки.

 

Если подставке сооб­щить вынужденное вращение во­круг вертикальной оси, как пока­зано на рисунке вектором ω ', то момент импульса L гироскопа по­лучит за время dt приращение dL ₁ — вектор, направленный за рисунок. Это приращение обу­словлено моментом M ₁ пары сил, действующих на ось гироско­па со стороны рамки. Гироскопические силы, действующие со стороны оси гироскопа на рамку, вызовут поворот последней вокруг горизонтальной оси 00'. При этом вектор L получит дополнительное приращение dL ₂, которое, в свою очередь, обусловлено моментом M ₂ пары сил, действующих на ось гиро­скопа со стороны рамки. В результате ось гироскопа будет по­ворачиваться так, что вектор L будет стремиться совпасть по направлению с вектором ω '.

Таким образом, за промежуток времени dt момент импульса L гироскопа получает приращение d L = d L ₁+d L ₂ = ( M ₁ + M ₂)dt При этом на рамку действует гироскопический момент

M' = -(M₁ + M₂)

 

Составляющая этого момента M' ₁ =- M ₁ вызывает поворот рамки вокруг горизонталь ной оси 00', другая составляющая M' ₂=- M ₂ противодействует повороту всей системы вокруг вертикальной оси (в отличие от предыдущего случая).

Гироскопический эффект лежит в основе разнообразных применений гироскопов: гирокомпас, гироскопический успоко­итель качки корабля, гироскопический стабилизатор и др.