Журнал “Начальная школа” 2008г. №3, стр. 80.

О.А. ХЛЕБНИКОВА

Журнал “Начальная школа” 2010г. №2, стр. 36

Https://n-shkola.ru/storage/archive/1407227124-1168118201.pdf

В любом курсе математики начальной школы изучению таблицы умножения уделяется большое внимание.

Усвоение табличных случаев происходит постепенно. В конце II класса школьники знакомятся с умножением и рассматривают только случаи табличного умножения с числами 9 и 8.

Для их усвоения они используют определение умножения (смысл действия умножения), переместительное свойство умножения и понятие увеличить в..., что создает условия для выполнения более содержательных заданий.

Нельзя не согласиться с Н.Б. Истоминой в том, что, усваивая смысл действия умножения, многие школьники непроизвольно запоминают табличные случаи.

В классе всегда есть ученики, которым необходима установка на запоминание. С этой целью в учебнике появляется запись: «Постарайся запомнить!» Эта инструкция встречается в учебнике 3 раза при изучении групп случаев: а) 9 7, 9 6, 9 5; б) 9 4, 9 3, 9 2; в) 9 8, 9 9.

На этапе самоконтроля полезно использовать карточки с выражениями на табличные случаи умножения и 2 конверта с надписями «Это я знаю» и «Это я пока не знаю».

Работа по учебнику «Математика» Н.Б. Истоминой направлена на развитие всех учащихся в процессе усвоения математического содержания, формирование положительной мотивации к обучению, обеспечение психологического комфорта на уроке и успешным овладением знаниями и умениями, необходимыми для продолжения обучения. Хочется отметить хорошее оснащение данного курса математики, в который входят: • учебники с I по IV класс, рабочие тетради, методические рекомендации для учителя; • тетради «Учимся решать задачи», «Наглядная геометрия»; • сборники контрольных работ для I–IV классов; • программа для I–IV классов; • наглядные пособия по математике.

 

 

Статья №2. «Нестандартный подход к обучению детей таблице умножения» БЕЛЕНЬКАЯ ТАТЬЯНА ЯКОВЛЕВНА, ГУРЕВИЧ ОЛЬГА

«Муниципальное образование: инновации и эксперимент» №1, 2013

https://cyberleninka.ru/article/n/nestandartnyy-podhodk-obucheniyu-detey-tablitse-umnozheniya/viewer

Перед современной школой стоит много задач, но основной и одной из самых важных задач, обозначенных в новых Федеральных Государственных образовательных стандартах, остаётся задача всестороннего развития ребёнка через сочетание учебной деятельности, в рамках которой формируются базовые знания, умения и навыки, с творческой и познавательной работой, которая непосредственно связанна с развитием способностей младшего школьника самостоятельно решать нестандартные задачи.

Нестандартный метод обучения детей таблице умножения «36 домиков за 36 дней» начинал разрабатываться и апробироваться ещё 10 лет назад. Многие педагоги согласятся с тем, что «старые» таблицы умножения имеют некоторые недостатки:

большой объём материала для запоминания, который построен так, что крайне тяжело использовать зрительную память ученика.

Предлагаемая нами переорганизация таблицы умножения облегчает запоминание и понимание, помогает развивать аналитическое мышление детей.

Новизна разработанного метода заключается в созданных для запоминания моделях закономерностей: «домики»–«улицы»–«город». Модели «домики» выстроены как последовательность «улицы» целого «города чисел».

Объясним суть нашего метода. На улицах «Города чисел» – 36 домиков. В каждом домике живёт тройка чисел: вверху живёт большой жилец, назовём его Целое. Внизу домика живут двое маленьких соседей. Например, Целое–20, соседи–4 и 5.

Мы не будет рассматривать домики, где соседи 1 или 10, потому, что их запомнить легко. Там, где один из соседей Единица, Целое равно её соседу, например: (5, 1, 5): 5 и 15 Из тройки цифр можно построить четыре примера: два на умножение и два на деление. К примеру, посмотри на домик, в котором живут 6, 3 и 2. Шесть –Целое, 3 и 2 –жильцы домика и соседи. 6 и 23.

 

После объяснения такого примера ребёнок сможет автоматически решить четыре примера, которые не нужно специально запоминать по отдельности:

 

3×2 =6, 2× 3 = 6, 6: 2 =3, 6: 3= 2.

 

В некоторых домиках соседи – близнецы (похожи), например: 9, 3, 3. Здесь будет рассмотрен только один пример на умножение и один на деление. Порядок запоминания каждого домика таков. К примеру, домик 8, 2, 4: 8 –Целое, 2 и 4 соседи.

 

Далее предлагается алгоритм данной работы.

 

Статья №3“Изучение внетабличного умножения коллективными способами обучения”

В.Ф. ЕФИМОВ, Л.В. ЕПИШИНА

Журнал “Начальная школа” 2008г. №3, стр. 80.

https://vk.com/doc144194164_545889767?hash=d2b5b9fd9dd5826f21&dl=eb6ab906ce08269790

Умение общаться по определенным нормам в учебной деятельности относится к коммуникативным свойствам личности учащихся.

Мы предлагаем изучать внетабличное умножение и деление по следующему плану.

I. Предварительный этап.

II. Взаимопередача тем и организация их усвоения через диалоговое общение школьников друг с другом в парах сменного состава.

III. Взаимные математические диктанты в парах сменного состава.

IV. Решение текстовых задач пройденных типов. V. Подведение итогов работы

I. Предварительный этап. На этом этапе происходит формирование умения общаться в парах постоянного состава, чему способствует работа со следющими памятками.

Для актуализации знаний, умений и навыков, повторения ранее изученного мы предлагали следующие устные задания и упражнения.

II. Взаимопередача тем и организация их усвоения через диалоговое общение школьников друг с другом в парах сменного состава. Для организации КСО при изучении этой темы нужно разделить класс (24 чел.) на 4 группы по 6 человек в каждой. Важно, чтобы в каждой группе было четное число участников, ведь только тогда можно образовать пары сменного состава.

III. Взаимные математические диктанты в парах сменного состава. На этом этапе школьники работают с последними заданиями, написанными на карточках. Учитель поясняет, что чем больше будет выполнено заданий, тем лучше.

IV. Решение текстовых задач изученных видов. Учитель проводит работу по поиску путей решения задач изученных видов.

V. Подведение итогов работы. — С каким количеством учеников вы поработали? Кто из партнеров хорошо спрашивал? С кем комфортно работать? Что вам понравилось, удовлетворило при работе с...? Кто из учеников пока еще не смог ре' шить задачу? Почему? Что вы им посоветуете? Далее учитель оценивает работы всего класса.

 

Статья №4. «Изучение таблицы умножения»

ТИМОФЕЕВА А. А.

https://infourok.ru/statya-izuchenie-tablici-umnozheniya-989564.html

Изучение табличного умножения и соответствующих случаев деления – центральная тема курса математики во II классе. Знанию таблицы умножения всегда придавали большое значение.

Формирование прочных вычислительных навыков табличного умножения и деления – одна из основных и сложных тем начального курса математики.

Готовясь к урокам, на которых учащиеся получат новые знания, стараюсь заинтересовать учащихся этим знанием, пробудить в них активное восприятие. Лучшему усвоению материала способствуют средства наглядности, опорные схемы, таблицы, которые применяю на каждом уроке.

Дидактические игры – одна из форм учебной деятельности. Поэтому на игру я отвожу всего несколько минут – от 5 до 10. Ценность дидактической игры я определяю не по тому, какую реакцию она вызывает со стороны детей, а учитываю, насколько она эффективно помогает решать учебную задачу применительно к каждому уроку. Далее приведу некоторые игры, с помощью которых ученик безболезненно усваивают таблицу умножения:

Игра «Живая математика»

У учащихся на груди табличка с цифрами от 0 до 9. Даю примеры на деление, например,72:9, 63:7, 32:8 и т.д. Встают ученики, у которых на груди таблички с цифрой 8, 9, 4 и т.д. Провожу игру в конце урока, т.к. она требует двигательную активность.

«Пальцевой счёт»

Для умножения чисел а и в, которые оба больше 5 и меньше 10, нужно вытянуть на одной и другой руке столько пальцев, на сколько единиц данные числа, каждые в отдельности, превышают 5. Сумма чисел вытянутых пальцев будет десятками произведения, а единицы - это произведение оставшихся загнутых пальцев.

Например: 7*8

(7-5; 8-5)

2 + 3 =5(это десятки)

2 * 3 = 6(это единицы) Значит, 7*8=56

Ещё пример: 6*8

6-5=1

8-5=3 1+3=4 –это десятки. А загнутых пальцев на левой руке -4, а на правой руке-2. Их произведение – это единицы. Значит, 6*8=48.

Формирование у учащихся навыков табличного умножения и деления - одна из главных задач обучения математике. Решение этой задачи возможно при усвоении систематической работы по закреплению навыков табличного умножения. В итоге такой работы учащиеся учатся находить результаты табличного умножения и деления не только правильно и осознанно, но и быстро.

 

 

Статья №5. «Элементы занимательности при изучении таблицы умножения»

Г.И. САЛАМАТОВА

Журнал “Начальная школа” 2004г. №10, стр. 56.

https://n-shkola.ru/storage/archive/1407239526-7717874.pdf

В изучении школьного курса математики, впрочем, как и любого другого предмета, су­ществуют объемные, достаточно однообраз­ные, но одновременно базовые основопола­гающие темы.

Важным звеном в изучении таблицы ум­ножения является формирование мотива­ции к данному виду деятельности, мотива­ции учения вообще, ориентированной на удовлетворение интересов, познавательной активности детей.

Необходимое условие формирования навыков табличного умножения — умение учителя организовать внимание учеников в начале урока.

Так, обычные по форме задания могут быть ориентированы на развитие активной познавательной деятельности, если сопровождаются необычной многосоставляющей инструкцией, предполагающей развитие логического мышления и творческий под­ ход к решению.

 

Для того чтобы освоение таблицы было более успешным, можно использовать раз­ личные приемы проверки знаний: — математические диктанты с использо­ванием веера; — карточки для парной работы (на од­ ной стороне карточки записаны 12 приме­ ров. На другой стороне — ответы. Около каждого примера сделано круглое отверс­тие. Первый ученик смотрит на пример, на­зывает ответ и вставляет карандаш в отвер­стие. Второй проверяет, правильно ли наз­ван ответ, и т.д. Затем ученики меняются ролями); — перфокарты; — маленькие карточки; с одной стороны написан пример, а с другой — ответ. Ученик смотрит на пример, называет ответ, перево­рачивает карточку и проверяет себя); — домино.

 

Статья №6. 4. «Использование многоцелевых заданий в процессе изучения внетабличного умножения и деления в начальной школе»

ШЕЛЫГИНА ОЛЬГА БОРИСОВНА

Научно-методический электронный журнал «Концепт». – 2016. – № S20.

file:///C:/Users/Admin/Downloads/ispolzovanie-mnogotselev-h-zadaniy-v-protsesse-izucheniya-vnetablichnogo-umnojeniya-i-deleniya-v-nachalnoy-shkole%20(1).pdf

Наиболее сложной темой при формировании вычислительных навыков является тема «Внетабличное умножение и деление». К внетабличным случаям относятся случаи умножения неоднозначных чисел с результатом, не превышающим ста, и соответствующие случаи деления (см. таблицу).

№	Вид приема	Суть приема, подробная запись	Теоретическая основа приема	Операции, входящие в прием
	20х3	20х3=2дес.х3=6дес.==60	Десяток – счетная единица	– Представление двузначного числа в виде разрядных единиц – табличное умножение – представление разрядных единиц двузначным числом
	23х4	23х4=(20+3)х4= =20х4+3х4= =80+12=92	Свойство умножения суммы на число	– Замена числа суммой разрядных слагаемых – свойство умножения суммы на число Умножение 1 вида (десятков) – табличное умножение – сложение двузначных чисел
	80:4	80:4=8 дес.:4=2 дес.=20	Десяток – счетная единица	– Представление двузначного числа в виде разрядных единиц – табличное деление – представление разрядных единиц двузначным числом
	96:3	96:3=(90+6):3= 90:3+6:3=30+2=32	Свойство деления суммы на число	– Замена числа в виде суммы разрядных слагаемых; – применение свойства деления суммы на число; – деление 3 вида; – табличное деление; – сложение разрядных слагаемых
	80:20	80:20=... 20*4=80	Взаимосвязь между компонентами и результатами арифметических действий	– Умножение 1 вида (десятков) – применение знания о взаимосвязи между компонентами и результатом умножения
	96:16	96:16= 16*6=96	Взаимосвязь между компонентами и результатами арифметических действий	– Умножение 2 вида (неразрядного двузначного числа наоднозначное) – применение знания о взаимосвязи между компонентами и результатом умножения

 

Знание данных приемов и умение решать соответствующие примеры должно быть на очень высоком уровне, так они являются основой изучения действий с трехзначными числами и далее – с многозначными.

Основным методом формирования вычислительных умений и навыков является метод упражнений.

Приведем примеры таких заданий в теме «Внетабличное умножение и деление».

Таким образом, использование многоцелевых заданий, то есть заданий, которые наряду с прямой обучающей целью преследуют другие образовательные цели, будет способствовать не только эффективному формированию вычислительных навыков внетабличного умножения и деления, но и развитию учеников в целом.

 

Статья №7. "Что такое умножение?"

БАЛАКИНА НАТАЛЬЯ ОЛЕГОВНА

https://urokimatematiki.ru/statya-chto-takoe-umnozhenie-2387.html

Умножение — одно из четырёх основных арифметических действий, бинарная математическая операция, в которой один аргумент складывается столько раз, сколько показывает другой. В арифметике под умножением понимают краткую запись сложения указанного количества одинаковых слагаемых. Например, запись обозначает «сложить три пятёрки», то есть. Результат умножения называется произведением, а умножаемые числа — множителями или сомножителями. Первый множитель иногда называется «множимое».

Умножение обозначается крестиком "×" или точкой "∙".

Знак умножения часто пропускают, если это не приводит к путанице. Например, вместо обычно пишут .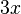

Свойства умножения

Умножение обладает следующими свойствами:

• коммутативностью (переместительный закон):
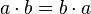
• ассоциативностью (сочетательный закон):
• дистрибутивностью (распределительный закон):

Ведущий российский методист и автор учебника по математике Истомина Н.Б., четко сформулировала особенности данной программы по исследуемой теме:

1) Первый этап - составление и усвоение таблиц умножения и деления включается в содержательную линию курса. Табличные случаи умножения учащиеся усваиваются в процессе изучения смысла умножения.

2) составление и усвоение таблицы умножения начинается со случаев умножения числа 9 (от более трудного к более лёгкому), что позволяет учащимся не только упражняться в сложении и вычитании двузначных и однозначных чисел с переходом через десяток, заменяя произведение суммой, но также сосредоточить внимание на сложных для запоминания случаях таблицы умножения: 9 · 8, 9 · 7, 9 · 6, по отношению к которым даётся установка на запоминание.

3) Учитывая, что не все дети могут непроизвольно запомнить таблицу умножения в процессе выполнения обучающих заданий, в учебнике, в определённой системе даются установки на запоминание трёх-четырёх табличных случаев. При этом установка на запоминание таблицы ориентирована на запоминание определённых табличных случаев.

4) Для организации самостоятельной работы учащихся рекомендуется фиксировать все случаи табличного умножения на карточке. Например, на одной стороне выражение, а на другой – его значение. Аналогично надо поступать со всеми случаями таблицы деления, что поможет учащимся действовать при запоминании табличных случаев умножения и деления, а также осуществлять самоконтроль».

В процессе исследования также познакомились с подходом к интересующей нас теме в системе обучения Л.В. Занкова по учебнику И.И. Аргинской. При изучении табличного умножения и деления, автором выделено только два этапа в работе учащихся:

1 этап – ознакомление с теоретическими сведениями, в том числе с порядком действия в выражениях. 2 этап – изучение таблицы умножения и деления с помощью таблицы Пифагора.

И.И. Аргинская выделяет два подхода – прямой и косвенный, давая им подробную характеристику, указывая на преимущества косвенного.

 

 

Статья №8. «Деление. Основные правила» (автора не нашла)

https://beginnerschool.ru/gen_rules/matem-gen_rules/delenie

Одним из простых арифметических действий является деление. Мы знаем, что умножение мы можем представить, как сложение числа самого с собой столько раз, на сколько нам надо его умножить.

Деление можно представить, как многократное вычитание.

12 ÷ 4 = 3

Число, которое мы делим, называется делимым, число на которое мы делим, называется делителем, а результат деления называется частным. В нашем примере делимое 12, делитель 4, а частное 3.

Деление можно проверить умножением:

3 × 4 = 12

А также деление можно проверить, многократным вычитанием:

12 – 3 – 3 – 3 – 3 = 0

Мы видим, что если из 12 вычесть 4 раза 3, то получится ноль. Значит, 12 на 4 делится без остатка.

Рассмотрим другой пример, разделим 13 на 4.

13 ÷ 4 = 3 (ост.1)

Проверим вычитанием:

13 – 3 – 3 – 3 – 3 = 1

Мы видим, что если из 13 четыре раза вычесть число 3, то останется 1. Наш пример называется делением с остатком. Здесь 13 – делимое, 4 – делитель, а 3 – неполное частное, 1 – остаток от деления.

Теперь проверим умножением:

3 × 4 + 1 = 13

Основные правила деления

1. НА НУЛЬ ДЕЛИТЬ НЕЛЬЗЯ!

2. Если делимое и делитель равны, то частное будет равно 1

3. Если делимое равно нулю, и частное будет равно нулю:

0 ÷ а = 0

4. Если делитель равен 1, то частное равно делимому:

а ÷ 1 = а

 

 

Статья №9. 9. «Как объяснить ребенку умножение и деление?»

ЕКАТЕРИНА УШАХИНА

https://deti.mann-ivanov-ferber.ru/2019/10/30/kak-obyasnit-rebenku-umnozhenie-i-delenie/

 

Подготовили для вас несколько советов и подборку книг, которые помогут разложить умножение и деление по полочкам.

Умножаем

Что такое умножение? При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым.

Умножение на 10, 100, 1000 Для того чтобы умножить целое число на 10, 100, 1000 и т. д., нужно просто дописать справа от этого числа один нуль (0), два нуля (00), три нуля (000) и т. д.

Делим

Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.

Деление как распределение. Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.

 

 

Статья №10. «Связь деления и умножения»

© budu5.com, 2020 (автора нет)

https://budu5.com/manual/chapter/1182

Смысл действия умножения состоит в том, что при умножении находится сумма одинаковых слагаемых.

Первое число при умножении показывает, какое слагаемое повторяют несколько раз.

Второе число при умножении показывает, сколько раз повторяют это слагаемое.

Результат умножения показывает, какое число получается.

6 • 4 значит, что число 6 повторяют 4 раза: 6 + 6 + 6 + 6 = 24

Первый множитель

Второй множитель

Произведение

Числа при умножении

Первый множитель

Второй множитель

Результат умножения, или Произведение