Практическая работа по геометрии по теме: «Движения»
Выполнила: ученица 9 класса «А»
Лушенкова Анастасия
СОДЕРЖАНИЕ РАБОТЫ:
· Введение
· Движение. Виды движения.
· Поворот.
· Параллельный перенос.
· Великие о симметрии
· Осевая симметрия.
· Центральная симметрия
· Скользящая симметрия
· Зеркальная симметрия.
· Симметрия в растениях.
· Симметрия в животном мире.
· Загадочные снежинки.
· Симметрия в архитектуре.
· Симметрия в литературе.
· Заключение.
· Литература.
«Симметрия – это идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство. »
 Г.Вейль
Г.Вейль
Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, также подчиняются принципам симметрии.
Движение плоскости – это отображение плоскости на себя, сохраняющее расстояния.
Виды движения:
1. Симметрия:
─ осевая,
─ центральная,
─ скользящая
─ зеркальная.
2. Параллельный перенос
3. Поворот.
Поворот- преобразование, при котором каждая точка А фигуры (тела) поворачивается на один и тот же угол α вокруг заданного центра О, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α - углом вращения.

Леонардо да Винчи считал, что главную роль в картине играют пропорциональность и гармония, под которыми он понимал симметрию.
Альбрехт Дюрер (1471-1528 г.г.) утверждал, что каждый художник должен знать способы построения правильных симметричных фигур.
Термин «симметрия» (σνμμετρυα, греч.) - соразмерность, пропорциональность, одинаковость в расположении частей.
Осевая симметрия - преобразование, при котором каждая точка А фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точку А1, при этом отрезок АА1 l, называется осевой симметрией.

Центральная симметрия- преобразование, переводящее каждую точку А фигуры (тела) в точку А1, симметричную ей относительно центра О, называется преобразованием центральной симметрии или просто центральной симметрией.

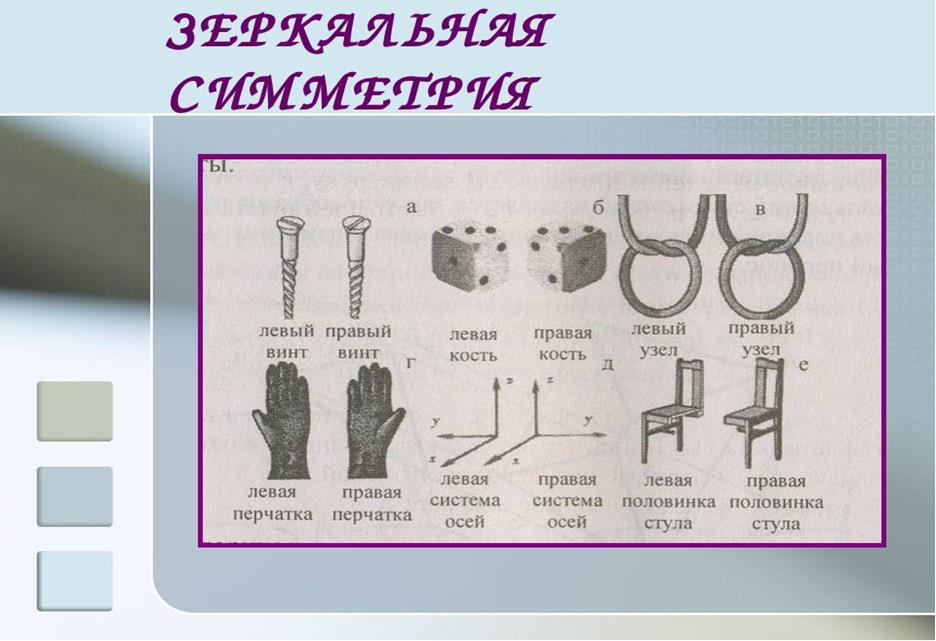
Зеркальная симметрия- если преобразование симметрии относительно плоскости переводит фигуру (тело) в себя, то фигура называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.

Внимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия. Ярко выраженной симметрией обладают листья, ветви, цветы, плоды. Зеркальная симметрия характерна для листьев, но встречается и у цветов. Для цветов характерна поворотная симметрия.



Симметрия встречается и в животном мире. Однако в отличие от мира растений симметрия в животном мире наблюдается не так часто. Рассмотрим, например, бабочку.

Снежинка – это группа кристалликов, образованная более чем из двухсот ледяных частичек.
Симметрия – это свойство кристаллов совмещаться друг с другом в различных положениях путём поворотов, параллельных переносов, отражений.



Нагляднее всего видна симметрия в архитектуре. Особенно блистательно использовали симметрию в архитектурных сооружениях древние зодчие. В сознании древнегреческих архитекторов симметрия стала олицетворением закономерности, целесообразности, красоты.



В литературных произведениях существует симметрия образов, положений, мышления. В греческой трагедии - виновный становится жертвой такого же преступления. В «Евгении Онегине» А. С. Пушкина мы наблюдаем симметрию положений: «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви»
Буквы русского языка тоже можно рассмотреть с точки зрения симметрии.