Если из одной точки в другую, имеющие разность потенциалов u, перемещать бесконечно малый заряд dq, то затрачивается работа, равная энергии:
.
Производная энергии по времени является мгновенной мощностью:
Следовательно, мгновенная мощность, поступающая в приемник, равна произведению мгновенных значений тока и напряжения. Она положительна при одинаковых знаках u и i и отрицательна при разных. Положительное значение мощности означает, что мощность поступает в приемник, отрицательное – возвращается в источник питания.
Энергию, потребляемую приемником за промежуток времени от t1 до t2, можно определить как
.
Измеряется мощность в ваттах (Вт), [Вт]=[В 
А], энергия – в джоулях (Дж), [Дж]=[В А с].
Пассивные элементы электрической цепи
Сопротивление
Сопротивлением называется идеализированный элемент цепи в котором происходит необратимый процесс преобразования электрической энергии в тепловую. Обозначение резистора приведено на рис. 1.1, буквенное обозначение – R или r.
Между напряжением на элементе, током и сопротивлением элемента существует соотношение:
, (1.2)
известное как закон Ома, экспериментально установленный немецким ученым Омом в 1826 г. Величина сопротивления измеряется в омах (Ом). [Ом] = [В/А].
Сопротивление всегда положительное, т.е., направления тока через сопротивление и напряжения на нем совпадают.
Величина, обратная сопротивлению
,
называется проводимостью. Измеряется проводимость в сименсах (См). [См] = [А/В].
Мгновенная мощность, выделяемая на сопротивлении, равна произведению мгновенных значений тока и напряжения:
,
т.е.,
Электрическая энергия, поглощаемая сопротивлением, равна:
|
|
Если ток постоянный (i = I = const), то
.
Емкость
Емкостью называется идеализированный элемент электрической цепи, приближенно заменяющий конденсатор, в котором накапливается энергия электрического поля. Буквенное обозначение емкости – С.
Величина емкости определяет, какой заряд q можно получить при заданном напряжении u:
(1.3)
или
Величина емкости измеряется в фарадах (Ф):
.
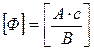Заряд и напряжение всегда имеют одинаковый знак, так как емкость С>0.
При изменении напряжения, приложенного к емкости, изменится в соответствии с (1.3) и электрический заряд. Подставив (1.3) в (1.1), получаем:
(1. 4.)
Не рассматривая процессы с позиций теории электромагнитного поля, отметим только, что в проводниках, соединенных с емкостью, будет протекать ток, величина которого определяется в соответствии с (1.4).
На основании выражения (1.4) напряжение на емкости 
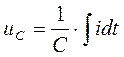
или
,
где предполагается, что до момента времени t процесс мог длиться сколь угодно долго, поэтому нижний предел интеграла принят равным (– 
). При t = 0 напряжение на емкости равно:
,
или
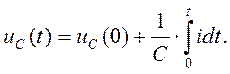(1.5)
Условное графическое обозначение емкости с положительными направлениями токов и напряжений приведено на рис. 1.5.
Мгновенная мощность, поступающая в емкость, равна:
,
откуда видно, что если 
, мгновенная мощность pc>0, т.е., емкость накапливает энергию (происходит заряд емкости), иначе происходит возврат энергии источнику питания (разряд емкости).
Энергия электрического поля в произвольный момент времени t определится по формуле: 
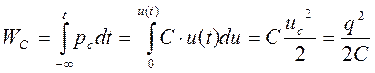. (1.6)
|
|
В выражении (1.6) предполагается, что при t = (– 
) напряжение на емкости С: Uc( 
= 0.
Индуктивность
Если контур из проводника поместить в переменное магнитное поле, то согласно закону электромагнитной индукции (Фарадея – Максвелла) в нем наводится электродвижущая сила (ЭДС), равная:
(1.7)
где Ф – магнитный поток, пронизывающий контур.
Измеряется поток в веберах (Вб). Согласно выражению (1.7)
.
Предположим, что контур состоит из нескольких витков (катушка), каждый из которых пронизывается своим потоком Фi.
Из (1.7) имеем:
, (1.7а)
где Y – потокосцепление, равное сумме всех потоков, пронизывающих все отдельные витки контура.
Когда все витки пронизываются одним потоком,
,
где w – число витков.
Если рассматривать изолированный контур с протекающим по нему током, то потокосцепление в этом случае носит название потокосцепления самоиндукции (соответственно ЭДС в (1.7) – ЭДС самоиндукции) и выражается как
. (1.8)
Коэффициент пропорциональности L между током и потокосцеплением называется индуктивностью самоиндукции или просто индуктивностью. В общем случае под индуктивностью будем подразумевать идеализированный элемент электрической цепи, приближающийся по своим свойствам к индуктивной катушке, которая способна накапливать энергию магнитного поля.
Измеряется индуктивность в генри (Гн).
.
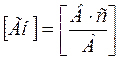Потокосцепление и ток имеют одинаковый знак, т.е., индуктивность всегда положительна (L>0).
Зависимость потокосцепления от тока в общем случае нелинейная, и параметр L зависит от тока. Зависимость потокосцепления от тока называется вебер-амперной характеристикой. В том случае, когда вебер-амперная характеристика линейна, индуктивность постоянна.
|
|
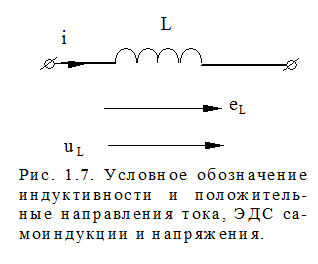
Условное графическое изображение индуктивности с указанием выбранных положительных направлений тока и ЭДС самоиндукции приведено на рис. 1.7. ЭДС самоиндукции и ток направлены в одну сторону, что учитывает знак минус в уравнении (1.7).
Если же опустить этот знак, направление ЭДС самоиндукции следует изменить на противоположное
 |
Для линейной индуктивности уравнение (1.7) примет вид:
. (1.9)
ЭДС самоиндукции eL компенсируется приложенным к индуктивности напряжением:
. (1.10)
Из (1.10) имеем:
или:
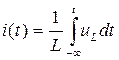
Нижний предел интегрирования, также как и для емкости, принят равным (– 
), так как до рассматриваемого момента времени t процесс мог длиться сколь угодно долго. При t = 0 ток в индуктивности равен:
,
следовательно:
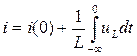(1.11)
Мгновенная мощность, поступающая в индуктивность, равна произведению тока и напряжения:
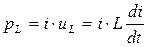(1.12)
Из (1.12) нетрудно видеть, что эта мощность может быть как положительной (при совпадении знаков тока и его производной), т.е., потребляемой индуктивностью, так и отрицательной (при несовпадении знаков тока и его производной), когда энергия возвращается во внешнюю цепь.
Энергия магнитного поля в произвольный момент времени t определяется по формуле:
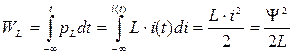(1.13)
Здесь учтено, что при t = (– 
) ток в индуктивности i(– ) = 0.