Множества мощности континуума
Теорема 1. Отрезок [0;1] несчётен.
Доказательство: Допустим противное, т.е. [0;1] – счётное множество. Тогда отрезок [0;1] представим в виде последовательности 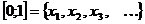 по теореме 1 предыдущего пункта.
по теореме 1 предыдущего пункта.
Разделим отрезок [0;1] на три равные части и возьмём ту из этих частей, которая не содержит точку 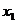 . Обозначим её через
. Обозначим её через 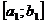 ,
, 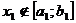 .
.
Разделим 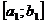 на три равные части и возьмём ту из них, которая не содержит
на три равные части и возьмём ту из них, которая не содержит 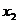 . Обозначим её
. Обозначим её 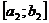 ,
, 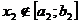 ,
, 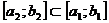 .
.
…………………………………………………………………
В результате получим последовательность вложенных отрезков 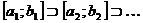 , где
, где 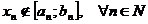 . По теореме о вложенных отрезках существует точка
. По теореме о вложенных отрезках существует точка 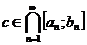 . Тогда
. Тогда 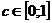 . Точка c должна быть либо
. Точка c должна быть либо 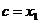 , либо
, либо 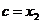 , и т.д.
, и т.д.
Но, так как 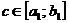 и
и 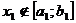 , то
, то 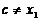 .
.
Так как 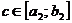 и
и 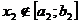 , то
, то 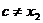 .
.
…………………………………….
Получаем 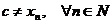 , следовательно,
, следовательно, 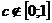 (c не совпадает ни с одной точкой отрезка). Мы получили противоречие, отсюда следует, что отрезок [0;1] не может быть счётным. Так как отрезок [0;1] – бесконечное множество, то [0;1] – несчётное множество. Теорема доказана.
(c не совпадает ни с одной точкой отрезка). Мы получили противоречие, отсюда следует, что отрезок [0;1] не может быть счётным. Так как отрезок [0;1] – бесконечное множество, то [0;1] – несчётное множество. Теорема доказана.
Определение 1. Множество, эквивалентное отрезку [0;1], называется множеством мощности континуума или множеством мощности c.
Примеры.
1) Любой отрезок [a;b] имеет мощность c, так как любые отрезки эквивалентны между собой, следовательно [a;b] ~ [0;1].
2) Любой интервал имеет мощность c, так как (a;b)=[a;b]\{a;b} ~ [a;b] по теореме 7.
3) Множество R имеет мощность c.
Можно установить взаимно однозначное соответствие между интервалами 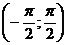 и
и 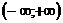 с помощью функции
с помощью функции 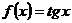 .
.
4) Множество иррациональных чисел J имеет мощность c.
J=R\Q ~ R по теореме 7, так как 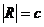 , а Q – счётное множество. Следовательно,
, а Q – счётное множество. Следовательно, 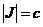 .
.
5) Множество трансцендентных чисел имеет мощность c.
Трансцендентные числа – это числа, которые не являются алгебраическими.
A - множество алгебраических чисел, T - множество трансцендентных чисел.
T=R\A ~ R по теореме 7, так как 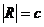 , а A – счётное множество. Следовательно,
, а A – счётное множество. Следовательно, 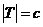 .
.
Теорема 2. Множество всех последовательностей из 0 и 1 имеет мощность c.
Доказательство: Пусть П - множество всех последовательностей из 0 и 1. Элементами этого множества являются последовательности 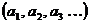 , где
, где 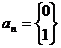 (или 0, или 1).
(или 0, или 1).
Каждое число x из отрезка [0;1] запишем в виде двоичной дроби, т.е.  , где
, где 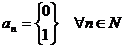 (для десятичной дроби соответствующее представление
(для десятичной дроби соответствующее представление 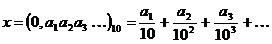 ). При этом числа вида
). При этом числа вида 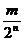 называются двоично рациональными числами. Они имеют два двоичных представления, а все остальные числа – единственное двоичное представление.
называются двоично рациональными числами. Они имеют два двоичных представления, а все остальные числа – единственное двоичное представление.
Пример: 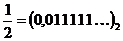 и
и 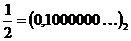 .
.
Сделаем проверку: 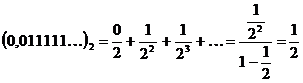 ,
,
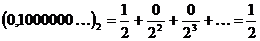 .
.
Для двоичных рациональных чисел будем брать только такое двоичное представление, у которого имеется бесконечное число единиц. В этом случае каждое число x из отрезка [0;1] будет иметь единственное двоичное представление. Каждому 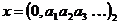 поставим в соответствие последовательность
поставим в соответствие последовательность 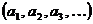 , но биекцию
, но биекцию 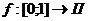 не получим, поскольку мы отбросили последовательности, у которых с какого-то места стоят одни нули (например,
не получим, поскольку мы отбросили последовательности, у которых с какого-то места стоят одни нули (например, 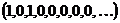 ).
).
Пусть 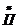 – такие последовательности из 0 и 1, у которых с какого-то места стоят одни нули. Таких последовательностей будет столько же, сколько двоично рациональных чисел. Но множество Q – счётное множество, следовательно, множество двоично рациональных чисел также является счётным множеством. Отсюда
– такие последовательности из 0 и 1, у которых с какого-то места стоят одни нули. Таких последовательностей будет столько же, сколько двоично рациональных чисел. Но множество Q – счётное множество, следовательно, множество двоично рациональных чисел также является счётным множеством. Отсюда 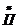 – счётное множество.
– счётное множество.
Определим отображение 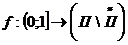 равенством: если
равенством: если 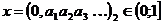 , то
, то 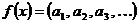 . Таким образом, f - биекция.
. Таким образом, f - биекция.
В таком случае 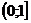 ~
~ 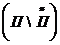 , т.е.
, т.е. 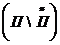 имеет мощность c. Определим мощность множества П.
имеет мощность c. Определим мощность множества П.
Пусть 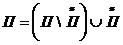 .
.
По теореме 5 предыдущего пункта 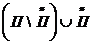 ~
~ 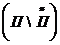 , так как
, так как 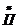 - счётное множество. Следовательно, П ~
- счётное множество. Следовательно, П ~ 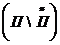 ,
, 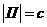 .
.
Теорема доказана.
Определение 2. Декартовым произведением счётного семейства множеств 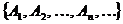 называется множество, элементами которого являются такие последовательности
называется множество, элементами которого являются такие последовательности 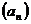 , что
, что 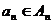 для каждого
для каждого 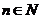 . Оно обозначается
. Оно обозначается 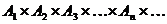 или
или 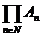 .
.
Пусть D={0,1}. Обозначим декартово произведение со счётным числом элементов 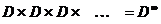 . Тогда П - множество всех последовательностей из 0 и 1,
. Тогда П - множество всех последовательностей из 0 и 1, 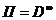 имеет мощность континуума.
имеет мощность континуума. 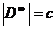 , но по теореме 6 предыдущего пункта декартово произведение конечного числа счётных множеств
, но по теореме 6 предыдущего пункта декартово произведение конечного числа счётных множеств 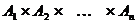 является счётным множеством.
является счётным множеством.
Теорема 3. Декартово произведение счётного семейства счётных множеств имеет мощность c.
Доказательство:
Пусть 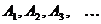 - счётные множества, докажем, что
- счётные множества, докажем, что 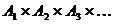 имеет мощность c.
имеет мощность c.
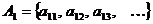 - счётно (теорема 1 предыдущего пункта)
- счётно (теорема 1 предыдущего пункта)
 - счётно (теорема 1 предыдущего пункта)
- счётно (теорема 1 предыдущего пункта)
…………………………………………………………………………
Получаем декартово произведение 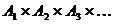 . Установим взаимно однозначное соответствие между элементами декартова произведения
. Установим взаимно однозначное соответствие между элементами декартова произведения 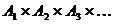 и множеством всех последовательностей натуральных чисел
и множеством всех последовательностей натуральных чисел 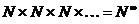 . Каждому элементу кортежа
. Каждому элементу кортежа 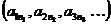 поставим в соответствие его номер во множестве
поставим в соответствие его номер во множестве 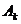 , где
, где 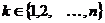 :
:
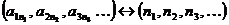 .
.
Таким образом, получена биекция 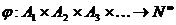 , следовательно,
, следовательно, 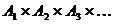 ~
~ 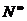 . Поэтому мощность множества
. Поэтому мощность множества 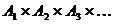 равна мощности множества
равна мощности множества 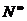 . Докажем, что множество всех последовательностей натуральных чисел
. Докажем, что множество всех последовательностей натуральных чисел 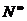 имеет мощность c. Для этого установим взаимно однозначное соответствие между множеством
имеет мощность c. Для этого установим взаимно однозначное соответствие между множеством 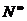 и множеством всех строго возрастающих последовательностей натуральных чисел V. Элементами множества V являются последовательности
и множеством всех строго возрастающих последовательностей натуральных чисел V. Элементами множества V являются последовательности  , где
, где 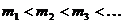 . Определим отображение
. Определим отображение 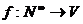 следующим образом: если
следующим образом: если 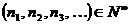 , то
, то 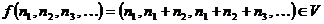 .
.
Пример: 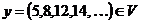 , найдём
, найдём  , такой, что
, такой, что 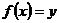 . Получаем
. Получаем 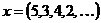 .
.
Сделаем проверку: 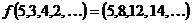 .
.
Таким образом, отображение 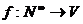 является биекцией.
является биекцией.
Пусть П – множество всех последовательностей из 0 и 1. Получим множество 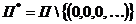 . Определим отображение
. Определим отображение 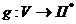 следующим образом: если
следующим образом: если 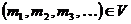 , то
, то 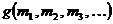 есть последовательность, у которой единицы стоят на местах
есть последовательность, у которой единицы стоят на местах 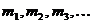 , а на всех остальных местах стоят нули.
, а на всех остальных местах стоят нули.
Пример: 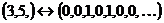
Отображение 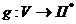 является биекцией. Следовательно, V ~
является биекцией. Следовательно, V ~ 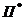 , откуда
, откуда 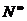 ~
~ 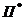 . Но
. Но 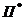 ~
~ 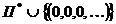 по теореме 5 предыдущего пункта, где
по теореме 5 предыдущего пункта, где 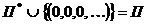 . Следовательно,
. Следовательно, 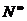 ~ П, но
~ П, но 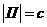 , отсюда
, отсюда 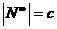 . Теорема доказана.
. Теорема доказана.
Теорема 4. Декартово произведение конечного или счётного семейства множеств мощности c имеет мощность c.
Доказательство: самостоятельно (Виленкин, учебник МГЗПИ, стр.20).
Следствие. Мощность множества точек плоскости (трёхмерного пространства) равна c.
Доказательство: Множество точек плоскости 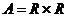 , по теореме 4
, по теореме 4 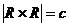 , следовательно,
, следовательно, 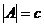 .
.
Множество точек трёхмерного пространства 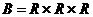 , по теореме 4
, по теореме 4 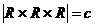 , следовательно,
, следовательно, 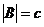 .
.
Упражнения:
1) Доказать, что объединение конечной или счётной совокупности множеств мощности c имеет мощность c.
2) Пусть 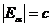
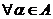 и
и 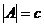 . Доказать, что
. Доказать, что 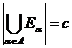 .
.
Сравнение мощностей. Теорема Кантора – Бернштейна
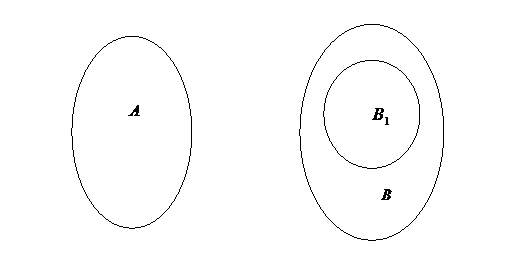
Определение 1. Говорят, что мощность множества A не превосходит мощности множества B и пишут 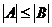 , если существует подмножество
, если существует подмножество 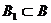 такое, что A ~
такое, что A ~  .
.
Задача. Доказать, что счётная мощность является наименьшей из мощностей бесконечных множеств.
Решение: Пусть B - произвольное бесконечное множество. Тогда по теореме 3 предыдущего пункта оно содержит счётное подмножество 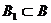 . Так как
. Так как  – счётно, то N ~
– счётно, то N ~ 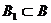 , отсюда по определению 1
, отсюда по определению 1 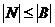 .
.
Определение 2. Если 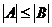 и множество A не эквивалентно множеству B, то говорят что мощность множества A меньше мощности множества B и пишут
и множество A не эквивалентно множеству B, то говорят что мощность множества A меньше мощности множества B и пишут 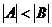 .
.
Пример. Рассмотрим множества N и [0;1]. 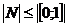 и множество N не эквивалентно [0;1], отсюда
и множество N не эквивалентно [0;1], отсюда 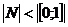 .
.
Мы получили, что мощность счётного множества меньше мощности континуума. Возникает вопрос, есть ли множества промежуточной мощности между 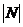 и c?
и c?
Теорема (Кантора-Бернштейна). Если каждое из двух множеств эквивалентно части другого, то эти множества эквивалентны.
Доказательство: Пусть множества A и B таковы, что A ~ 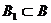 и B ~
и B ~ 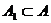 . Тогда существуют биекции
. Тогда существуют биекции 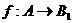 ,
, 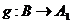 . Рассмотрим
. Рассмотрим 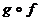 , это инъективное отображение из A в A.
, это инъективное отображение из A в A.
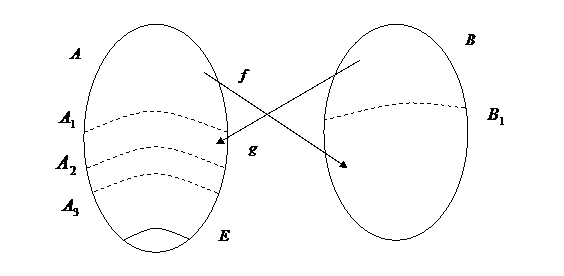
Найдём 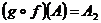 , имеем A ~
, имеем A ~  . Как связаны множества
. Как связаны множества  и
и 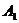 ? Очевидно,
? Очевидно, 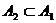 .
.
Аналогично, 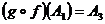 , имеем
, имеем 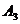 ~
~ 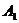 ,
, 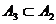 .
.
……………………………………………………………..
В результате получаем последовательность множеств
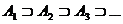 и
и  ~
~ 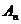 для всех
для всех 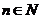 .
.
Возьмём 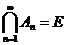 .
.
Тогда  .
.
Аналогично, 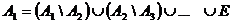 .
.
Обозначим
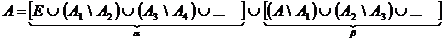 ,
,
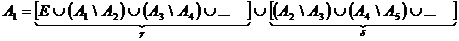 .
.
Имеем 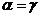 . Докажем, что
. Докажем, что 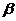 ~
~ 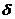 .
.
Рассмотрим биекцию 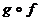 :
: 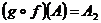 ,
, 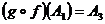 , тогда
, тогда  .
.
Аналогично,  .
.
………………………………………………
Таким образом, отображение 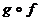 взаимно однозначно отображает
взаимно однозначно отображает 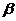 на
на 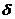 .
.
Определим отображение h из A в 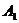 :
:
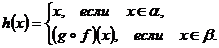
Очевидно, h - биекция A на 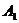 . Значит, A ~
. Значит, A ~ 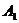 , но, по условию,
, но, по условию, 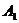 ~ B. Следовательно, A ~ B. Теорема доказана.
~ B. Следовательно, A ~ B. Теорема доказана.
Следствие. Если мощности множеств 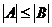 и
и 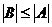 , то
, то 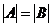 .
.
Доказательство:
Так как 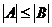 , то существует множество
, то существует множество 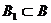 , такое, что A ~
, такое, что A ~  .
.
Так как 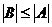 , то существует множество
, то существует множество 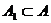 , такое, что B ~
, такое, что B ~ 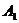 .
.
Отсюда по теореме Кантора-Бернштейна A ~ B, т.е. 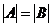 .
.