План работы
| Номер задания | Блок содержания | Контролируемое знание/умение | Уровень сложности | Тип задания | Примерное время выполнения (в мин) | Максималь- ный балл за выполнение | Код планируемо- го результата в кодификаторе |
| Числа и величины | Понимание десятичного состава числа | Б | ВО | 1.1 | |||
| Числа и величины | читать, записывать; числа от нуля до 1000; | Б | ВО | 1.1 | |||
| Арифметические действия | Составлять числовое выражение по заданному условию | Б | КО | 2.6 | |||
| Арифметические действия | вычислять значение чис-лового выражения (содержащего 2-3 арифм. действия, со скобками и без скобок). | Б | КО | 2.5 | |||
| Числа и величины | Решение практической задачи, связанной со сравнением величин | Б | ВО | 1.5 | |||
| Геометрические величины | Представление о пери-метре прямоугольника | Б | КО | 5.3 | |||
| Арифметические действия | Понимание смысла арифметических действий | Б | ВО | 2.4 | |||
| Арифметические действия | Нахождение неизвестно-го компонента арифме-тического действия | Б | КО | 2.3 | |||
| Работа с текстовыми задачами | Оценивание величины при решении практической задачи | Б | РО | 3.1 | |||
| Числа и величины | Перевод одних единиц измерения в другие | Б | КО | 1.5 | |||
| Работа с текстовыми задачами | Нахождение времени начала, конца, продол-жительности события | Б | КО | 3.4 | |||
| Пространственные отношения. Геометрические фигуры | Распознавание четырехугольников | Б | ВО | 4.2 | |||
| Геометрические величины | Нахождение периметра и площади прямоугольника | Б | РО | 5.3 | |||
| Работа с данными | читать несложные готовые таблицы; | Б | КО | 6.1 | |||
| Работа с текстовыми задачами | Решение задач, связан-ных с бытовыми, жиз-ненными ситуациями | Б | РО | 3.2 | |||
| Дополнительная часть | |||||||
| Пространственные отношения. Геометрические фигуры | Овладение основами пространственного воображения. Описывать взаимное расположение предметов в пространстве и на плоскости. | П | КО | 4.1 | |||
| Пространственные отношения. Геометрические фигуры | распознавать и называть геометрические тела: куб, шар; | П | КО | 4.6 | |||
| Пространственные отношения. Геометрические фигуры | взаимное расположение предметов в пространстве и на плоскости | П | КО | 4.1 | |||
| Работа с текстовыми задачами | Интегрированное при-менение знаний: дейст-вия с величинами, ариф-метические действия, анализ реальности ответа | П | РО | 3.2.1 | |||
| Б – 16 П - 4 | ВО - 5 КО-10 РО– 4 | 40 мин | 25 балла 15 – 17 8 – П |
1 вариант итоговой работы по математике в 3 классе
|
|
Учебный год
1. Пётр Николаевич разложил кафельную плитку по ящикам. Сколько плиток у Петра Николаевича?
ð 307 ð 407 ð 317
2. В подъезде дома, где живет Миша, расположены квартиры от № 260 до № 281. Сколько номеров квартир этого подъезда содержат цифру 7 в разряде десятков?
ð 12 номеров 10 номеров 3 номера
3. Среднюю продолжительность жизни сосныы можно узнать, если из числа 600 вычесть произведение 25 и 4 и результат увеличить на 30. Составь числовое выражение продолжительности жизни сосны. Считать не нужно.
|
|
4. Выполни действия и найди значение выражения
91: (26 – 19) ∙ 4 = ______
5. К новогоднему школьному празднику надо купить 4 упаковки шаров и 3 гирлянды. Достаточно ли 500 рублей на эту покупку, если одна упаковка шаров стоит 32 рубля, а одна гирлянда — 120 рублей?
ð недостаточно, не хватит 12 рублей
ð достаточно, останется 12 рублей
ð достаточно, покупка стоит ровно 500 рублей
6. Света хочет обшить разноцветной тесьмой покрывало прямоугольной формы для куклы. Размеры сторон покрывала 30 см и 50 см. Сколько сантиметров тесьмы ей потребуется?
7. К Маше на день рождения пришли 7 девочек и 5 мальчиков. В вазе на столе лежало 52 конфеты. Какое наименьшее число конфет нужно ещё положить в вазу, чтобы конфет досталось всем гостям поровну?
ð 12 4 8
8. Коля задумал число, увеличил его в 3 раза и получил 72. Какое число задумал Коля?
9. В прошлом году для подкормки лосей в заповеднике заготовили 150 стогов сена, а в этом году — в три раза больше. На сколько стогов сена больше заготовили в этом году, чем в прошлом? Составь числовое выражение по заданному условию.
|
|
10. Заполни пропуски
4 дм 3 см = _____см 1 ч. = _____ мин. 69 дм = _____ м ____см
50 ч. = ___сут.___ч. 31 мм = ____см____мм 1 нед.1 сут.= _____сут.
11. Друзья вышли на лыжную прогулку в лес в 10 часов 30 минут, а вернулись домой в 14 часов 30 минут. На дорогу до леса и обратно они затратили 1 час. Сколько времени длилась лыжная прогулка по лесу?
12. Сколько четырёхугольников на рисунке?
ð 3 4 5
13. На рисунке длина стороны клеточки равна 1 см. Дострой прямоугольник так, чтобы его периметр был равен 14 см.
Вычисли площадь получившегося прямоугольника. Ответ:___________________________
_________________________________
_________________________________
14. 
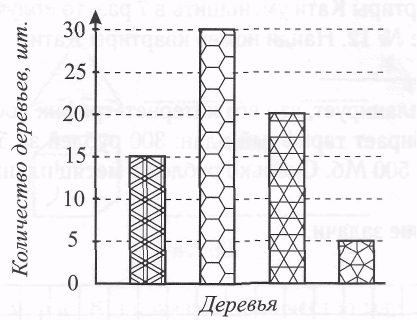На диаграмме показано количество каштанов, лип, дубов и акаций в городском саду. Известно, что в саду больше всего дубов, меньше всего каштанов, а лип больше, чем акаций. Сколько акаций в городском саду?
Ответ:____________________________________
15. Для доставки гостей к ближайшей железнодорожной станции после пикника был заказан микроавтобус, в котором 11 посадочных мест. При наличии большого количества людей микроавтобус делает рейсы только с полной загрузкой. Сколько человек перевезёт микроавтобус последним рейсом, если всего на пикнике было 60 гостей??
Дополнительная часть
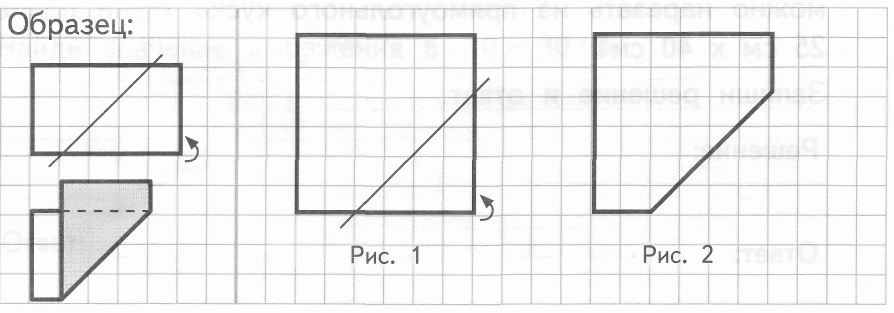
16. На уроке технологии дети складывали фигурки из бумаги.
В образце показано, что получилось, когда лист бумаги перегнули по отмеченной линии. На рисунке 1 дана фигура и линия сгиба. Покажи на рисунке 2, как будет выглядеть эта фигура после сгибания. Закрась отогнутую часть.
17. 
Гена сложил из деталей конструктора ракету. Запиши номера и количество фигур, которые он использовал.
1) конус
2) куб
3) шар
4) цилиндр
5) прямоугольник
Ответ:_______________________________________________________________________
18. Из этих двух деталей конструктора сложили фигуру.
Какая это фигура? Отметь ответ. Придумай, как доказать, что верно выбрал.
19. На ужин мама решила поджарить 7 блинчиков с творогом. Блинчики надо жарить 2 мин на одной стороне и 1 мин - на другой стороне. На сковородке помещаются 4 блинчика. За какое наименьшее время мама поджарит все блинчики? Запиши ответ и объясни его.
Ответ:_______________________________________________________________________
Объяснение:__________________________________________________________________
2 вариант по математике в 3классе 2016-2017уч. год
1. 
Алёна увлекается плетением из бисера. Для своего будущего изделия она разложила бисер по мешочкам. Сколько бисера у Алёны?
ð 350 штук ð 320 штук ð 305 штук
2. Петя идет по улице Московской мимо дома №121 к дому №137. Сколько домов этой улицы, мимо которых должен пройти Петя, содержат в своём номере цифру 3 в разряде единиц?
ð 8 домов 2 дома 10 домов
3. Среднюю продолжительность жизни бурого медведя можно узнать, если разность 125 и 30 уменьшить в 5 раз и результат увеличить на 31. Составь числовое выражение средней продолжительности жизни медведя. Считать не нужно
4. Вычисли
81: (23 – 14) ∙ 7 =_____
5. Для призов на конкурс надо купить 10 линеек и 6 ручек. Достаточно ли 500 рублей на эту покупку, если одна линейка стоит 25 рублей, а одна ручка стоит 30 рублей?
ð недостаточно, не хватит 70 рублей
ð достаточно, останется 70 рублей
ð достаточно, покупка стоит ровно 500 р.
6. 
Катя обшила тесьмой с трёх сторон два квадратных кармашка на юбочке. Каждая сторона кармашка равна 8 см. Сколько сантиметров тесьмы ей потребовалось?
Ответ:___________________________________________
________________________________________________
7. В классе 23 ученика. На столе учителя лежало 60 чистых тетрадей. Какое наименьшее число тетрадей нужно ещё добавить учителю, чтобы тетрадей досталось поровну всем ученикам?
ð 14 9 6
8. Если возраст мамы уменьшить в 4 раза, то получится возраст дочки. Дочке 9 лет. Сколько лет маме?
9. В авторемонтной мастерской работают 72 слесаря, а механиков в 6 раз меньше. На сколько слесарей больше, чем механиков? Составь числовое выражение по заданному условию.
10. Заполни пропуски
6 дм 2 см = _____см 2 ч = ______мин 25 дм = ___м____см
38 ч = ___сут.___ч 43 мм = ___см___мм 1 нед.2 сут.=___сут.
11. Представление в театре начинается в 16 ч 30 мин и продолжается 120 мин. В котором часу заканчивается спектакль?
Ответ: в______________ч______________мин.
12. Сколько четырёхугольников на рисунке?
ð 3 4 5
13. 
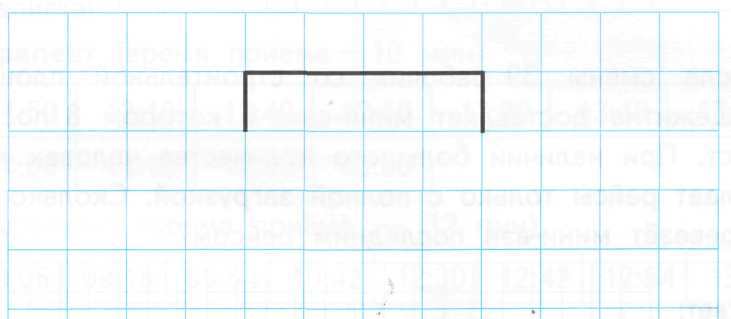На рисунке длина стороны клеточки равна 1 см. Дострой прямоугольник так, чтобы его периметр был равен 14 см.
Вычисли площадь получившегося прямоугольника.
Ответ:___________________________
_________________________________
_________________________________
14. На диаграмме показан рост девочек Насти, Светы, Полины, Вики. Самая высокая девочка — Полина, самая низкорослая — Света. Вика ниже Насти. Найди рост Вики.
Ответ:_______________________________________
15. После смены 39 рабочих со строительной площадки в общежитие доставляет мини-вэн, в котором 8 посадочных мест. При наличии большого количества человек мини-вэн делает рейсы только с полной загрузкой. Сколько человек перевезёт мини-вэн последним рейсом?
Дополнительная часть
16. На уроке технологии дети складывали фигурки из бумаги. В образце показано, что получилось, когда лист бумаги перегнули по отмеченной линии. На рисунке 1 дана фигура и линия сгиба. Покажи на рисунке 2, как будет выглядеть эта фигура после сгибания. Закрась отогнутую часть.
17. 
Гена сложил из конструктора замок. Запиши номера и количество фигур, которые он использовал.
1) куб
2) прямоугольник
3) шар
4) цилиндр
5) конус
Ответ:_______________________________________________________________________
18. 
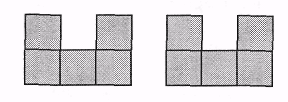Из этих двух деталей конструктора сложили фигуру.
Выбери эту фигуру. Отметь ответ. Придумай, как доказать, что верно выбрал.
19. Миша сделал из бумаги 8 самолётиков. Половину самолётиков он отдал другу и сделал себе ещё столько же самолётиков, сколько отдал, и ещё 3. Сколько теперь самолётиков у Миши?
Запиши ответ и объясни его.
Ответ:_______________________________________________________________________
Объяснение:__________________________________________________________________
________________________________________________________________________________________________________________
Система оценивания выполнения отдельных заданий и итоговой работы в целом
Задания базового уровня любого формата, оцениваются по одной шкале, повышенного уровня – по другой шкале.
Результаты выполнения основной и дополнительной частей работы НЕ суммируются.
За верное выполнение каждого из 15 заданий (№№ 1-15) основной части работы выставляется 1 - 2 балла. Таким образом, за выполнение основной части работы максимально можно получить 17 баллов.
За выполнение каждого из четырёх заданий повышенного уровня сложности (№№16-19) в зависимости от правильности и полноты ответа выставляется от 0 до 2 баллов, т.е. максимально ученик может получить 8 баллов. Результаты выполнения этих заданий позволяют составить представление о возможностях учащихся справляться с нестандартными учебными и практическими ситуациями, которые требуют применения математики.
Учащийся достиг уровня базовой подготовки, если он справился не менее чем с 65% заданий базового уровня, включенных в итоговую работу.
Если учащийся получает за выполнение основной части работы не менее 11 баллов за выполнение базовых заданий (из 17). то считается, что он достиг уровня базовой подготовки по курсу математики 3-го класса отвечающего требованиям ФГОС НОО.
При получении 12-17 баллов можно констатировать, что учащийся имеет достаточно прочную базовую подготовку. Это означает, что он демонстрирует не только наличие опорной системы знаний, необходимой для успешного продолжения образования, но и произвольное использование сформированных учебных действий
Более детально подход к проверке и оценке выполнения отдельных заданий рассматривается в «Рекомендациях для учителя по проверке и оценке выполнения работы».
Результаты выполнения группы заданий базового уровня сложности, включенных в работу, используются для оценки достижения третьеклассником уровня обязательной базовой подготовки, которая является необходимой основой, обеспечивающей возможность успешного дальнейшего образования.