Среди множества функций есть функции, значения которых с увеличением аргумента только возрастают или только убывают. Такие функции называются возрастающими или убывающими.
Функция y = f(x) называется возрастающей в промежутке а < x < b, если для любых х1 и х2, принадлежащих этому промежутку, при х1 < х2 имеет место неравенство f(x1) < f(x2).
Функция y = f(x) называется убывающей в промежутке а < x < b, если для любых х1 и х2, принадлежащих этому промежутку, при х1 < х2 имеет место неравенство f(x1) > f(x2).
Как возрастающие, так и убывающие функции называются монотонными, а промежутки, в которых функция возрастает или убывает, – промежутками монотонности.
Например, функция 
при 
монотонно убывает, а при 
монотонно возрастает. Функция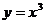 
на всей числовой оси монотонно возрастает.
Предел функции в точке
2.1. Число А называется пределом функции f(x) при 
, если для любого числа ε>0 можно указать такое δ>0, что для любого 
, удовлетворяющего неравенству 
, выполняется неравенство 
. В этом случае пишут 
.
Если число А1 (число А2) есть предел функции y = f(x) при x, стремящемся к a так, что х принимает только значения, меньшие (большие) а, то А1 (А2) называется левым (правым) пределом функции f(x) в точке а. При этом соответственно пишут 
.
2.2. Постоянная величина b называется пределом функции ƒ(x) при x стремящемся к x0 (x→ x0), если для всех x сколь угодно мало отличающихся от x0 соответствующие значения функции ƒ(x) сколь угодно мало отличаются от b. То есть, при x→ x0, ƒ (x) →b,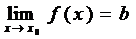 
.
Замечание:
x может стремится не только к конечному x0, но и к бесконечности (x → ∞), и к нулю (x→0).
Функция f(x) называется бесконечно малой при , если 
.
Функция f(x) называется бесконечно большой при , если 
.
Теоремы о пределах
1 Если функция y= ƒ(x) имеет предел при x→0, то этот предел единственный.
2 Предел постоянной величины равен этой же постоянной, независимо от того, к чему стремится переменная.
, где С= const (1)
3 Предел алгебраической суммы конечного числа функций, имеющих конечные пределы, равен алгебраической сумме пределов всех слагаемых.
(2)
3 Предел произведения конечного числа функций, имеющих конечные пределы, равен произведению пределов сомножителей.
(3)
4 Предел частного двух функций, имеющих пределы, равен отношению пределов числителя и знаменателя, если предел знаменателя не равен нулю.
, где 
(4)
5 Постоянный множитель можно выносить за знак предела:
, где С= const (5)
Виды неопределенностей
1 
, 
, 
Например:
2 
, 
, 
Например:
3 
, , 
Например:
4 
, 
,
Например:
, где c = const
5 
, 
, 
Например:
Замечательные пределы
Первый замечательный предел: 
. (6)
Второй замечательный предел: 
. (7)
Если предел отношения двух бесконечно малых величин равен единице, то эти бесконечно малые величины называются эквивалентными.
Непрерывность функции
Ещё одним важным свойством является свойство непрерывности функции.
Рассмотрим примеры. Поставили кипятить воду. С течением времени температура воды повышается. Но как? Постепенно, то есть за малый промежуток времени, температура повысится незначительно.
Аналогично, небольшим промежуткам времени отвечают малые изменения температуры воздуха.
Наглядное представление о непрерывной функции состоит в том, что график такой функции можно начертить одним непрерывным движением, не отрывая карандаша от бумаги. На рисунке 1 изображена некоторая непрерывная функция.
Функция f(x) называется непрерывной в точке х = х0, если:
1 эта функция определена в точке х = х0 (то есть определённому значению аргумента х, равному х0, соответствует вполне определённое значение функции y, равное y0);
2 приращение функции в точке х0 стремится к нулю при 
, то есть
(8)
Геометрически непрерывность функции означает, что ординаты двух точек графика сколь угодно мало отличаются друг от друга, если достаточно мало отличаются их абсциссы. Часто пользуются другим определением непрерывности функции в точке.
Функция f(x) называется непрерывной в данной точке х0, если её предел в точке х0 существует и равен значению функции в этой точке.
Функция называется непрерывной на отрезке 
, если она непрерывна в каждой точке этого отрезка.
Исследуем на непрерывность функцию .
Решение. Пусть приращение аргумента х равно Δх, тогда функция y получит какое-то приращение Δy. Имеем
,
откуда
.
Очевидно, что при любом фиксированном значении х и при Δх, стремящемся к нулю, Δy также стремится к нулю, то есть функция непрерывна при любом значении х.
Вычисление пределов
Рассмотрим некоторые примеры вычисления пределов функций.
№ 1 Вычислить пределы:
a) 
;
б) 
;
в) 
;
г) 
.
Решение
а) Пользуясь теоремами о пределах, получим
б) 
Для того чтобы раскрыть неопределенность 
в данном пределе поделим почленно числитель и знаменатель на x в старшей степени в данном выражении, т.е. на x4. Получим
в) Применяя теоремы о пределах, обнаруживаем, что 
, то есть, знаменатель дроби обращается в нуль. Значит, теорему о пределах дроби здесь пока применить нельзя. Но поскольку и предел числителя 
, то для того, чтобы раскрыть получившуюся 
неопределенность, мы разложим числитель и знаменатель на множители
Сокращение дроби на (x-1)здесь возможно, поскольку x→1, но x ≠ 1и множители (x-1) в нуль не обращаются, а являются эквивалентными бесконечно малыми величинами при x→1, отношения которых равно единице
г) 
. Если воспользоваться теоремами о пределах и подставить x = 2 в правую часть вместо x, то получим неопределенность . Неопределенность можно устранить, если выделить и сократить эквивалентные бесконечно малые в числителе и знаменателе. Разложим знаменатель на множители, а в числителе вынесем за скобку 3. Получим
Здесь дробь можно сократить на x-2, так как x→2, но x≠2.
Вопросы для повторения
1 Сформулируйте определение функции.
2 Что называется областью определения функции?
3 Что называется областью значения функции?
4 Какими способами может быть задана функция?
5 Какие функции называются чётными?
6 Какие функции называются нечётными?
7 Какие функции называются возрастающими?
8 Какие функции называются убывающими?
9 Дайте определение предела функции.
10 Перечислите свойства пределов.
11 Перечислите виды неопределённостей.
12 Запишите первый и второй замечательный пределы.
13 Дайте определение функции непрерывной в точке и на отрезке.