Лекция № 8
Вероятность. Теоремы сложения и умножения вероятностей
План
1 Элементы комбинаторики.
2 Элементы теории вероятностей.
Элементы комбинаторики
Группы, составленные из каких-либо элементов, называются соединениями.
Различают три вида основных соединений: размещения, перестановки и сочетания.
Задачи, в которых производится подсчёт возможных различных соединений, составленных из конечного числа элементов по некоторому правилу, называются комбинаторными. Раздел математики, занимающийся их решением, называется комбинаторикой.
Размещения
Размещениями из n элементов по m элементам называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.
Число размещений из n по m элементам обозначается символом  и вычисляется по формуле:
и вычисляется по формуле:
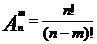 (1)
(1)
Перестановки
Перестановками из n элементов называются такие соединения, которые отличаются друг от друга лишь порядком следования элементов.
Число перестановок обозначают символом Pn. Перестановки представляют собой частный случай размещения и вычисляются по формуле:
 (2)
(2)
Сочетания
Сочетаниями из n элементов по m называются такие соединения, каждое из которых содержит n элементов, взятых из данных m элементов, и отличается от другого хотя бы одним элементом, обозначается  и вычисляется о формуле:
и вычисляется о формуле:
 (3)
(3)
Пример 1.1. Вычислить:
1)  ;
;
2) Р4.
Решение. Применяем формулы (2) и (3):
1) 
2) 
Элементы теории вероятностей
Основные определения
Если некоторое событие при данных условиях может произойти или не произойти, то оно называется случайным.
Количественной оценкой возможности появления данного случайного события является его вероятность. Вероятность события А обозначается символом Р(А).
Классическое определение вероятности: вероятность события А равна отношению числа случаев m, благоприятствующих ему из общего числа n равновозможных, единственно возможных и несовместимых, к числу n, то есть:
 (4)
(4)
Вероятность любого события не может быть меньше нуля и больше единицы, то есть:
 (5)
(5)
Невозможному событию соответствует вероятность равная нулю, а достоверному – вероятность равная единице.
Если произведена серия из N опытов, в каждом из которых могло появиться или не появиться некоторое событие А, то частотой события А в данной серии опытов называется отношение числа опытов М, в которых появилось событие А, к общему числу произведённых опытов. Частота события
W(A) =  (6)
(6)
Пример 2.1 В ящике находится три белых два чёрных шара. Из ящика вынимается наугад один шар. Найти вероятность того, что этот шар будет белым.
Решение. Событие, состоящее в появлении белого шара, обозначим через А.
Общее число случаев n = 3+2 = 5.
Число случаев, благоприятствующих наступлению события А, то есть m = 3.
Имеем:
 .
.
Пример 2.2 В урне находятся 10 белых и 6 чёрных шаров. Из урны наудачу вынимается два шара. Найти вероятность того, что оба шара будут белыми.
Решение. Обозначим через А событие, состоящее в появлении двух белых шаров. Общее число возможных случаев n, найдём по формуле числа сочетаний (3) из общего числа 16 шаров по два, то есть
 .
.
Определим число случаев m, благоприятствующих событию А:

Искомая вероятность появления двух белых шаров определится при помощи равенства (4):

Пример 2.3 При перевозке 1000 арбузов разбитых оказалось 15 штук. Какова частость разбитых арбузов?
Решение. В соответствии с формулой (6), где M = 15, N = 1000, найдём:

Пример 2.4 На отдельных карточках написаны буквы а, р, к. у, ч. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Найти вероятность того, что получится слово «ручка».
Решение. Число всех возможных исходов испытания, то есть n, равно в данном случае числу перестановок из пяти букв:
Р5 = 5! = 120.
Из всех перестановок только одна образует слово «ручка», поэтому m = 1, n = 120, а вероятность искомого события будет
 .
.
Теоремы сложения и умножения вероятностей
Теорема сложения