Производство с одним переменным фактором.

Производственная функция (общий случай, линейная, кобба-дугласа, CES (постоянной эластичности замены)). производство с одним переменным фактором. закон убывающей предельной производительности.

1. Производственная функция и ее свойства.

Под производством в современной микроэкономике понимается деятельность по использованию факторов производства (ресурсов) с целью создания продукта или услуги и достижения наилучшего результата. Если объем использования ресурсов известен, то производитель стремится получить максимальный результат. Если же задан результат, который необходимо достичь, например, объем выпуска, то минимизируется объем используемых ресурсов.

В процессе производства используются факторы производства: труд (), капитал (), земля и другие. Можно выделить составные части каждого фактора и рассматривать их как самостоятельные факторы. Например, в факторе труд могут быть выделены труд менеджеров, инженеров, сборщиков, и т.д.

В экономической теории выделяют первичные факторы производства, которые в соответствие с теорией факторов производства (ее связывают с именем французского экономиста Жана Б. Сэя) создают новую стоимость. К ним относятся труд, капитал, земля и предпринимательские способности. Вторичные факторы не создают новую стоимость. В современном производстве возрастает роль энергии и информации. Им присущи признаки первичных и вторичных факторов.

В моделях процесса производства - в производственных функциях, учитываются два основных фактора: труд и капитал . И это позволяет проанализировать важнейшие связи и зависимости, существующие в процессе производства, без упрощения их реального содержания.

Производственная функция выражает технологическую взаимосвязь между конечным выпуском и затратами факторов производства и . В неявном виде она записывается следующим образом:

,

где - форма функции,

- максимальный выпуск, который можно получить при используемой технологии и имеющемся количестве факторов производства ( и ). В производственной функции все параметры – выпуск, затраты труда и капитала измеряются в натуральных единицах (выпуск в метрах, тоннах и т.п., затраты в человеко-часах, станко-часах и т.п.).

Примером производственной функции, в явном виде представляющей зависимость между выпуском и затратами факторов производства, является функция Кобба-Дугласа:

, ,

где - эффективность технологии,

- частная эластичность выпуска по труду,

- частная эластичность выпуска по капиталу.

Функция была выведена математиком Ч. Коббом и экономистом П. Дугласом в 1928 году на основе статистических данных обрабатывающей промышленности США. Эта, сегодня широко известная функция, обладает рядом замечательных свойств. Ниже проанализируем экономический смысл ее параметров. Функция Кобба-Дугласа описывает экстенсивный тип производства.

Если используется факторов производства, то производственная функция имеет вид:

,

где - количество используемого -го фактора производства.

Свойства производственной функции:

1. Производственные факторы являются взаимодополняющими. Это значит, что если хотя бы один фактор равен нулю, то и выпуск равен нулю:

Исключение составляет функция: . В соответствии с такой функцией можно использовать только труд или только капитал и выпуск будет не равен нулю. Например, грузчик в своей работе может не использовать капитал и выполнит определенный объем работ.

2. Свойство аддитивности означает, что можно объединить факторы производства и 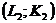. Но объединение целесообразно лишь в том случае, если выпуск после объединения превышает сумму выпусков до объединения факторов производства. .

3. Свойство делимости означает, что процесс производства может осуществляться в сокращенных масштабах, если выполняется следующее условие: , где - любое положительное число. При уменьшении числа рабочих и объема капитала вдвое выпуск продукции сократится не более чем на половину. Данное свойство не выполняется на малых предприятиях, где производственная деятельность при уменьшающихся масштабах либо невозможна, либо неэффективна. Такое свойство характерно для функции, отражающей процесс производства в отрасли или в народном хозяйстве.

Отдача от масштаба. Если затраты и изменяются в раз, как правило возрастают, то выпуск изменяется в раз:

При этом, если , то имеем неизменную отдачу от масштаба; если - возрастающую отдачу от масштаба; если , то имеет место убывающая отдача от масштаба.

Изокванта (или кривая постоянного продукта (isoquant) представляет собой график производственной функции. Точки на изокванте представляют бесконечное множество комбинаций факторов производства, использование которых обеспечивает одинаковый выпуск продукции.

Изокванты характеризуют процесс производства подобно тому, как кривые безразличия процесс потребления. Они имеют отрицательный наклон, выпуклы относительно начала координат. Изокванта (см. рис. 24), лежащая выше и правее другой изокванты, представляет больший объем выпускаемой продукции (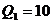 изделий, , ). Однако в отличие от кривых безразличия, где общую полезность набора товаров точно измерить нельзя, изокванты показывают реальный уровень производства. Совокупность изоквант, каждая из которых представляет максимальный выпуск продукции, получаемый при использовании факторов производства в различных сочетаниях, называется картой изоквант (isoquant map).

Реальная изокванта с выпуском 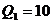представлена на рис 24 а в трехмерном пространстве. Ее проекция отмечена пунктирной линией и перенесена на рис. 24 б. Если используются отмеченные сочетания факторов производства 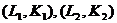, но применяется более прогрессивная технология, то выпуск будет равен . Но проекция у изокванты с таким выпуском будет той же, что и у изокванты с меньшим выпуском. Экономисты располагают на плоскости изокванту с большим выпуском (рис. 24 б) выше и правее изокванты с меньшим выпуском. На рис. 24 а взаимосвязь между выпуском и затратами нарушается: выпуск получен с большими затратами труда и капитала, чем 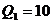. Ниже будет показано, как на расположение изокванты оказывает влияние применяемая технология и ее параметры.

Эффективность технологии (параметр в функции Кобба-Дугласа) можно представить графически следующим образом (рис. 25).

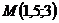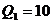В точках и выпуск один и тот же . На рис. 25 б изокванта представляет более эффективную технологию, так как затраты на единицу продукции здесь ниже, чем на изокванте на рис. 25 а.

Производство с одним переменным фактором.

В зависимости от ситуации, складывающейся на рынке, фирма то расширяет, то сокращает объем производства. В краткосрочном периоде трудно изменить объем используемых факторов производства – установить новое оборудование, расширить производственные площади и т.п. Состояние и параметры факторов производства в краткосрочном периоде определены предшествующими решениями фирмы. В долговременном периоде все факторы производства являются переменными.

Проанализируем часто встречающийся на практике случай, когда в краткосрочном периоде объем используемого капитала остается постоянным, а затраты труда изменяются. Труд является переменным фактором. Производственная функция имеет вид: 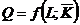, где .

Построим кривую общего продукта (,),рис. 26. До точки объем производства увеличивается быстрее затрат труда, потому что на каждого работника или на единицу труда приходится в сравнении с последующими периодами больший объем капитала. После этой точки темп роста общего продукта замедляется, достигает максимума в точке и затем начинает снижаться. В точке 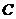выпуск и затраты растут одинаковыми темпами.

Кривая общего продукта иллюстрирует зависимость между выпуском и затратами одного переменного фактора.

Проведем секущую линию через точки и 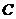(см. рис. 27). Точка имеет координаты ; в точке 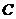прирост затрат труда позволяет увеличить выпуск, ее координаты . Таким образом,

,

Отношение - измеряет предельную производительность труда на дуге. Предельная производительность труда представляет собой отношение прироста выпуска продукции к вызвавшего его приросту затрат труда. Предельную производительность можно измерить тангенсом угла, который образует секущая с положительно направленной осью абсцисс: .

Считается, что прирост выпуска обеспечен приростом затрат труда, хотя его величина зависит от объема применяемого капитала.

Если , то точка 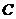перемещается по дуге в точку , а секущая занимает положение касательной. Тогда, предельная производительность труда в точке измеряется величиной - первой частной производной производственной функции по переменному фактору - труду:

.

Предельную производительность труда в любой точке можно измерить тангенсом угла, который образует касательная к кривой общего продукта с положительно направленной осью абсцисс: . Частное изменение выпуска при изменении затрат труда составляет . Аналогично можно записать для капитала .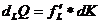

Построим кривую предельной производительности (рис. 26). До точки предельная производительность труда растет потому, что по мере вовлечения в производство дополнительных работников все более полно используются производственный мощности фирмы и выпуск растет быстрее затрат труда. На отрезке каждый последующий дополнительный работник обеспечивает уменьшающийся прирост продукта, так как вооруженность труда капиталом уменьшается. В точке выпуск достигает максимального значения, приращение продукта – предельный продукт становится равным нулю: . После точки увеличение затрат труда начинает сокращать выпуск, дополнительные работники становятся избыточными, а предельный продукт - отрицательным.

Средний продукт труда или средняя производительность труда измеряется отношением выпуска к затратам труда. В точке она равна: . Средний продукт труда можно измерить тангенсом угла, который образует линия, соединяющая точку на кривой общего продукта с началом координат, и положительно направленной осью абсцисс. Построим кривую среднего продукта, рис. 26.

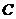Средний продукт труда растет до точки . На этом отрезке с вовлечением в процесс производства дополнительной единицы труда к средней добавляется предельная, превышающая предыдущее значение предельной производительности. После точки 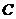средняя производительность снижается. На этом отрезке с вовлечением в процесс производства дополнительной единицы труда к средней добавляется предельная величина, которая меньше любого предыдущего значения средней. В точке 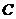средняя и предельная производительность равны: . Касательная линия к точке 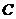и линия, соединяющая ее с началом координат, совпадают.

Кривые и являются зеркальным отражением кривых средних общих и предельных издержек фирмы .

Если внедрять новую технологию, то кривая общего продукта изменяет свою форму (см. рис. 28).