В [3], [2] изложена физика явлений ХД, ФСМ и ФКМ, выведены основные уравнения и соотношения. Аналитические выражения, описывающие совместное действие ХД и ФСМ выведены только для некоторых частных случаев. Например, в [20] дано выражение для уширения гауссовского импульса при совместном действии ХД и ФСМ. Для полного описания действия на импульсы ФСМ и ФКМ в дисперсионной среде требуется численное решение.
Уравнение распространения оптических импульсов в световоде для огибающей импульса A – медленно меняющейся амплитуды:
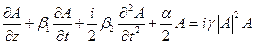, (10)
где 
– описывает движение огибающей импульса с групповой скоростью 
,
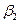[пс2км-1] – характеризует дисперсию групповых скоростей (ДГС), 
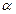[км-1] – постоянная затухания, 
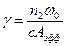[Вт-1км-1] – нелинейный коэффициент.
Это уравнение справедливо для импульсов с длительностью ≥ 0.1 пс и шириной спектра такой что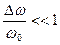 
.
Оно описывает распространение оптических импульсов в одномодовых световодах. Учитывает эффекты оптических потерь, хроматической дисперсии и нелинейности показателя преломления. Но оно не учитывает эффектов ВКР и ВРМБ. Если пиковая мощность импульса больше некоторого порогового уровня, под действием ВКР и/или ВРМБ, энергия этого импульса может быть передана стоксову импульсу. Он будет распространяться в прямом и/или обратном направлении. Тогда в световоде будут распространяться импульсы на разных длинах волн вызванные нелинейным рассеянием. Следовательно, будет возникать ФКМ. Похожая ситуация наблюдается когда два модулированных излучения на разных длинах волн вводятся в световод. Распространение импульсов описывается уже системой уравнений. Этот случай будет рассмотрен ниже.
Прежде чем решать уравнение удобно перейти в систему координат, движущуюся с групповой скоростью импульса (бегущие координаты)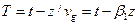 
, тогда уравнение примет вид:
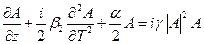. (11)
Введем нормированную амплитуду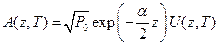 
, где P0 – пиковая мощность начального импульса. Следовательно, уравнение примет вид:
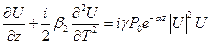. (12)
U(z, T) – форм функция. По изменению этой функции во времени при распространении на z удобно следить за изменением формы импульса.
Рассмотрим два простых случая. В первом случае на импульс, распространяющийся в световоде, действует только ДГС:
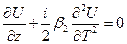. (13)
Во втором случае действует только ФСМ:
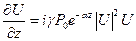. (14)
Дисперсия групповых скоростей
Решение уравнения (13)
Решение уравнения (13) рассмотрим на примере гауссовского импульса:
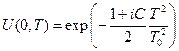. (15)
Необходимо выполнить Фурье преобразование начального условия.
, 
.
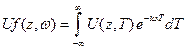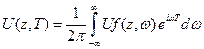В вычислениях будем пользоваться тем, что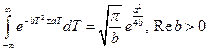 
.
Пусть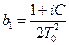 
, 
, 
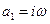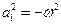, тогда 
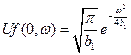. Уравнение (13) примет вид:
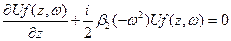. (16)
Его решение:
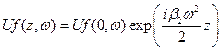. (17)
Далее необходимо взять обратное преобразование Фурье.
, 
, 
;
;
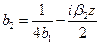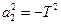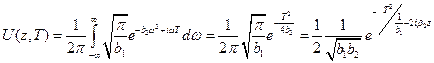Подставляем значения констант, получаем:
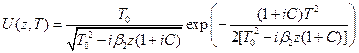. (18)
Отметим, что ω в вычислениях – частота спектрального разложения Фурье. Ее нельзя путать с несущей частотой ω0. Реальные спектральные компоненты это ωсп = ω0 + ω. Т.е. По спектру, полученному преобразованием Фурье можно судить о ширине и форме спектра.
Фазовая самомодуляция
Решение уравнения (14)
Выполняем интегрирование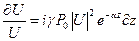 
, получаем: 
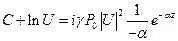, где C – константа интегрирования, которую находим из начальных условий: 
, 
.
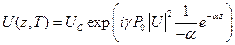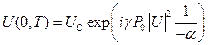Имеем: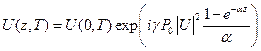 
. Обозначаем 
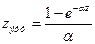. Окончательно: 
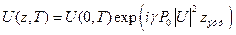. (19)
Если потери отсутствуют zэфф в (19) заменяется на z.
Отклонение от центральной частоты:
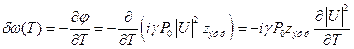. (20)
Величина zэфф экспоненциально стремится к 1/α при увеличении z. Тем самым действие ФСМ сильно ограничивается потерями световода. Действует ФСМ на относительно небольшом участке световода. Если потери в световоде составляют 0.2 дБ/км, то после прохождения 50 км, zэфф будет приблизительно равняться 50% от своего максимального значения, при прохождении 240 км – 90%.
Фазовая кросс-модуляция
Фазовая кросс-модуляция для двух волн, одновременно распространяющихся в волоконном световоде, описывается системой уравнений:
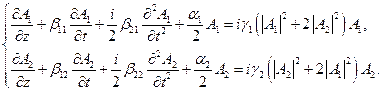(21)
Для форм функций в бегущих координатах относительно первой волны, эта системы примет вид:
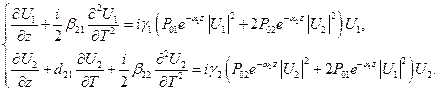(22)
Где расстройка групповых скоростей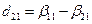 
, 
, 
, 
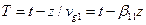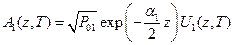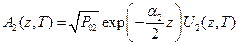. P01 и P02 – пиковые мощности начальных импульсов.
Часто для анализа решения системы необходимо знать расстояние, при прохождении которого импульсы перестают перекрываться, тогда, как в начальный момент было полное перекрытие двух импульсов во времени. Длина дисперсионного разбегания импульсов выражается через длительность импульса и расстройку групповых скоростей:
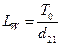. (23)
Решение уравнения (12)
Уравнение (12) не решается аналитически в общем случае. В этом случае можно воспользоваться численными методами: [3], [7], [11], [12], [13]. Используются 1) разностные методы и 2) псевдоспектральные методы. Вторые, как правило, на порядок быстрее при той же точности. Для уравнения распространения импульсов в нелинейной среде с дисперсией часто используется Фурье-метод расщепления по физическим факторам (Split-Step Fourier Transform method) с использованием алгоритма быстрого Фурье-преобразования (Fast Fourier transform). В [7] производится сравнение этого метода с другими численными методами.
Численные методы
Решение уравнения распространения оптических импульсов - Численное решение уравнения
Фурье-метод расщепления по физическим факторам с использованием алгоритма быстрого Фурье-преобразования.
 |
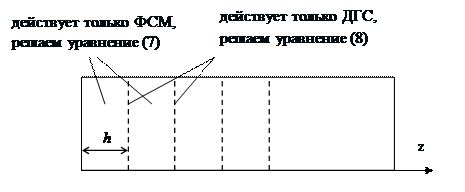В [3] изложены основы численного моделирования для решения уравнения распространения оптических импульсов. В данной части будет изложено описание численного решения уравнения (12) Фурье-методом разделения по физическим факторам.
Описание метода
Суть метода заключается в том, что
а) для уравнения (13): ХД физически относится к явлению, описывающему распространение различных спектральных компонент с разными скоростями. В Фурье-пространстве действие дисперсии описывается простыми законами. Выражение для скорости распространения спектральных компонент:
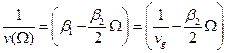. (24)
б) для уравнение (14) Нелинейность не действуют раздельно на спектральные компоненты. Только когда, согласно спектру, импульс собран во времени и можно наблюдать огибающую импульса, можно просто говорить о действии нелинейности показателя преломления (действие описано во введении). Действие нелинейности показателя преломления проявляется и легко описывается в пространстве времени.
Принято в два шага при численном решении уравнения распространения при прохождении импульса от точки 1 к точке 2. На первой стадии действует нелинейность б). Получаем промежуточное решение. Далее, полученное промежуточное решение как начальное подставляем в уравнение а). Полученное решение служит начальным условием для дальнейшего счет. Вычисление заканчивается, когда пройдет весь отрезок длины счета.
Оптический световод
Рассмотрим оптический световод, имеющий конечную длину. Ось z направим вдоль световода. Согласно методу, длина световода разбивает на малые части. Пусть h [км] – шаг по z, всего N шагов чтобы пройти всю длину L = N·h [км]. Для простоты будем считать разбиение L равномерным.
Параметры световода для λ = 1550 нм:
β2 = -22.1 пс2км-1; γ = 1.13 Вт-1км-1; α = 0.046 км-1.
Задание импульсов
Задается огибающая оптических импульсов U(z,T) – форм функция и P0 [Вт] – пиковая мощность импульса при z = 0. P(z,T) = | U(z,T) |2. В некоторых случаях задается частотная модуляция импульсов. Длительность импульсов T0 от 1 пс. Необходимо определиться с отрезком времени наблюдения импульсов. Это отрезок времени, в течение которого можно наблюдать проявление интересующих нас эффектов и составляет порядок 5 T0.