1. Построение математической модели электрической цепи.
Для послекоммутационной цепи составляем по законам Кирхгофа систему дифференциальных уравнений, дополненную уравнениями связи:
, 
, 
.
Для рассматриваемой цепи с двумя узлами и тремя ветвями она содержит три уравнения по законам Кирхгофа и одно уравнение связи:
| (1) |
2. Составление дифференциального уравнения цепи.
Систему (1) путем последовательного исключения переменных сводим к дифференциальному уравнению второго порядка относительно 
.
Из третьего и первого уравнений системы (1)
| (2) |
| (3) |
Дифференцируя (3) и подставляя результат во второе уравнение (1), получим
| (4) |
Согласно классическому методу расчета, решение дифференциального уравнения (4) ищем в виде двух составляющих – принужденной и свободной:
| (5) |
3. Определение начальных условий.
3.1. Независимые начальные условия, т.е. ток в катушке индуктивности 
и напряжение на конденсаторе 
, определяем расчетом установившегося процесса в докоммутационной цепи (ветвь 1 разомкнута):
| (6) |
3.2. Зависимые начальные условия, т.е. значения остальных токов и напряжений (1) при подстановке в нее независимых начальных условий:
| (7) |
Решение (7) дает:
Значения производных 
и 
на момент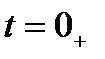 
необходимы для последующего определения постоянных интегрирования.
4. Определение принужденной составляющей.
В случае подключения цепи к источнику постоянной ЭДС принужденный режим совпадает с установившемся режимом (при 
).
Для послекоммутационной цепи после окончания переходного процесса
| (8) |
Такой же результат получается из уравнения (4), если учесть, что при постоянной ЭДС
4 Определение свободной составляющей.
Свободная составляющая является решением однородного дифференциального уравнения, которое для рассматриваемого примера имеет вид
| (9) |
Запись свободной составляющей определяется видом корней характеристического уравнения: при вещественных корнях
| (10) |
при комплексно-сопряженных
| (11) |
где 
- корни характеристического уравнения; 
- постоянные интегрирования.
4.1. Определение корней характеристического уравнения.
Характеристическое уравнение, соответствующее дифференциальному уравнению (4), имеет вид
| (12) |
При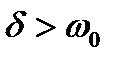 
его корни будут вещественными отрицательными:
 
| (13) |
а переходный процесс – апериодический.
При 
корни уравнения комплексно-сопряженные с отрицательной вещественной частью:
| (14) |
а переходный процесс – колебательный. В последнем случае 
называют коэффициентом затухания, а 
- частотой свободных колебаний.
Для нашей цепи, согласно уравнению (4),
Корни характеристического уравнения
| (15) |
вещественные отрицательные, переходный процесс апериодический.
4.2. Определение постоянных интегрирования.
Для определение постоянных интегрирования используем начальные условия: значение искомой переменной и ее производной в момент времени 
, полученные в п. 3.
Общее решение для напряжения 
| (16) |
а для его производной:
| (17) |
Уравнения (16) и (17) для момента времени образуют систему для определения постоянных интегрирования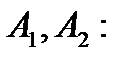 
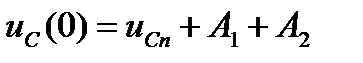
| (18) |
Для рассматриваемого примера система уравнений (18) имеет вид
Решение уравнения дает
5. Получение решений для всех физических переменных цепи.
Решение для напряжения на конденсаторе получим подстановкой найденных значений принужденной и свободной составляющей в общее выражение (5):
Правильность решения проверяют на соответствие граничным условиям:
Напряжение и токи на остальных элементах цепи, определяется из исходной системы (1) после подстановки в нее найденного решения.
На рис. 2 приведены графики напряжений 
, 
, 
, 
. Для момента времени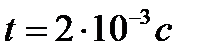 
проверено выполнение II закона Кирхгофа:
Рис. 2
На рис. 3 приведены графики токов 
, 
, 
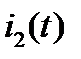. Для момента времени 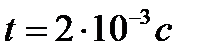проверено выполнение I закона Кирхгофа:
Рис. 3