2.6.1 Исходные данные: подкрановая балка крайнего ряда пролетом 12 м под два крана грузоподъемностью Q=32/5 т. Режим работы 8К – особо тяжелый. Пролет здания 36 м. Материал балки сталь С255 по ГОСТ 27772-88 по /3 табл. 50/. Для принятой марки стали находим /3 табл. 51/ расчетное сопротивление стали Rу= 24 кН/см2. Rср. = 14 кН/см2.
2.6.2 Нагрузки на подкрановую балку: из п. 2.2.3 на стр. наибольшее вертикальное усилие на колесе  кН; вес тележки Gт = 150 кН; тип кранового рельса КР-70.
кН; вес тележки Gт = 150 кН; тип кранового рельса КР-70.

Рисунок 2.22 - Схема крановой нагрузки
Для кранов тяжелого режима работы поперечное горизонтальное усилие на колесе при расчете подкрановых балок  кН.
кН.
Расчетные значения усилий на колесе крана определяем по формуле с учетом коэффициента надежности по назначению 

 (2.71)
(2.71)
где k1 = 1,1 и k2 = 1,1 коэффициенты динамичности, принимаемые по 4.9 /1/.
 коэффициент перегрузки;
коэффициент перегрузки;  коэффициент сечений по п. 4.17 /1/.
коэффициент сечений по п. 4.17 /1/.
 кН
кН
 кН
кН
2.6.3 Определение расчетных усилий
Максимальный момент возникает в сечении, близком к середине пролета. Загружаем линию влияния мамонта в среднем сечении, устанавливая краны не выгоднейшим образом. Для пролета балки 12 м определение Мmax cм. Рис. 2.23

Рисунок 2.23 - Линия влияния момента Мmax
Расчетный момент от вертикальной нагрузки:
 кН м (2.72)
кН м (2.72)
где уi – ординаты линий влияния;  = 1,05 – учитывает влияние собственного веса подкрановой конструкции и временной нагрузки на тормозной площадке.
= 1,05 – учитывает влияние собственного веса подкрановой конструкции и временной нагрузки на тормозной площадке.
Расчетный момент от горизонтальной нагрузки  кН м
кН м
Для определения максимальной поперечной силы загружаем линию влияния поперечной силы на опоре рис. 2.24

Рисунок 2.24
Расчетные значения вертикальной и горизонтальной поперечных сил:
 кН
кН
 кН
кН
3.6.4 Подбор сечения балки
Определение высоты балки
Из условия общей прочности определяем требуемый момент сопротивления.
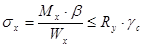

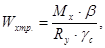 (2.73)
(2.73)
где 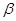 - коэффициент учитывающий влияние горизонтальных поперечных нагрузок на напряжение в верхнем поясе подкрановых балок.
- коэффициент учитывающий влияние горизонтальных поперечных нагрузок на напряжение в верхнем поясе подкрановых балок.
 (2.74)
(2.74)
где hб – высота балки в пределах  ;
;

hт – ширина сечения пормозной конструкции
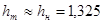

 см3
см3
Задаемся гибкостью стенки  табл. 7.2 /2/
табл. 7.2 /2/
Оптимальная высота балки
 см
см
Минимальная высота балки из условия жесткости
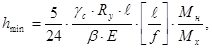 (2.75)
(2.75)
где Е – модуль упругости, Е = 2,06 · 104 кН/см2;  - относительный прогиб.
- относительный прогиб.
Для 8К  = 600; Мн – момент от загружения балки одним краном при п = 1,0. Мн – определим по линии влияния на рис. 2.24; сумма ординат линии влияния при нагрузке от одного крана
= 600; Мн – момент от загружения балки одним краном при п = 1,0. Мн – определим по линии влияния на рис. 2.24; сумма ординат линии влияния при нагрузке от одного крана 
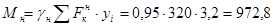 кН м
кН м
 см
см
Принимаем hб = 1580 мм
Задаемся толщиной полок tв.п. = 2,5 см; tн.п. = 2,5 см, тогда 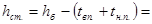
 мм
мм
Из условия среза стенки силой Qx
 см
см
Принимаем стенку толщиной 1,2 см
Размеры поясных листов определяем по формуле
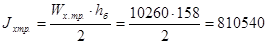 см4
см4
 см4
см4
 см2
см2
Принимаем пояс из листа сечения 25 х 500 мм, Ап = 125 см2
Устойчивость пояса обеспечена, так как

По полученным данным компонуем сечение балки рис. 2.25
2.6.5 Определение геометрических характеристик подкрановых конструкций
Подкрановую балку принимаем с одинаковыми размерами поясов. Находим положение центра тяжести тормозной балки
 , (2.76)
, (2.76)
 |
Рисунок 2.25 - Сечение подкрановой балки и тормозной балки
где  - сумма статических моментов элементов тормозной балки относительно оси у-у подкрановой балки;
- сумма статических моментов элементов тормозной балки относительно оси у-у подкрановой балки;  - сумма площадей сечения элементов тормозной балки.
- сумма площадей сечения элементов тормозной балки.
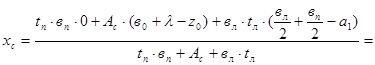
 см
см
Считаем, что левый конец стенки тормозной балки совпадает с центром тяжести швеллера.
Момент инерции подкрановой балки
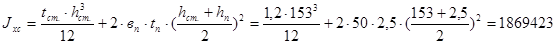 см4
см4
Момент сопротивления подкрановой балки
 см3
см3
Статический момент полусечения подкрановой балки
 см3
см3
Момент инерции тормозной балки


 см4
см4
Момент сопротивления наиболее напряженного волокна верхнего пояса подкрановой балки в точке А
 см3
см3
2.6.6 Проверка прочности подкрановой балки
Прочность подкрановой балки проверяется по нормальным и касательным напряжениям. По нормальным напряжениям в верхнем поясе от действия вертикальных сил и горизонтальных сил.
 кН/см2
кН/см2
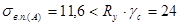 кН/см2
кН/см2
Прочность стенки на действие касательных напряжений на опоре обеспечена, т.к. принятая толщина стенки больше определенной из условия среза.
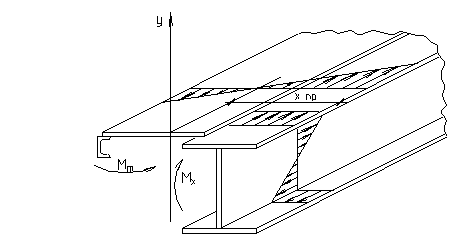
Рисунок 2.26 - Эпюры напряжений
Проверка прочности стенки подкрановой балки.
На уровне сопряжения пояса со стенкой выполняется проверка по приведенным напряжениям.
 (2.77)
(2.77)
где  - напряжения от общего изгиба в стенке балки на уровне сопряжения стенки с поясом.
- напряжения от общего изгиба в стенке балки на уровне сопряжения стенки с поясом.
 кН/см2
кН/см2
 - локальные напряжения
- локальные напряжения
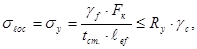 (2.78)
(2.78)
где  с – коэффициент который для сварных балок равен 3,25;
с – коэффициент который для сварных балок равен 3,25; 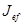 - суммарный
- суммарный
момент инерции верхнего пояса и кранового рельса.
 см4;
см4;  см4
см4
 см
см
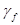 - коэффициент увеличения нагрузки на колесе.
- коэффициент увеличения нагрузки на колесе.  для режима работы 8К.
для режима работы 8К.
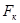 -расчетная нагрузки на колесе без учета динамичности
-расчетная нагрузки на колесе без учета динамичности  кН
кН
 кН/см2 <
кН/см2 <  кН/см2
кН/см2
 |
Рисунок 2.27
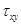 - касательные напряжения в стенке
- касательные напряжения в стенке
 кН/см2 <
кН/см2 <  кН/см2
кН/см2
 кН/см2 <
кН/см2 <  кН/см2
кН/см2
Пояса со стенкой при режиме работы 8К соединяются сварными швами с проваром на всю глубину стенки. В этом случае швы считаются равнопрочными со стенкой и их можно не рассчитывать.
При наличии тормозных конструкций общая устойчивость балки обеспечена и не требует проверки.
2.6.7 Местная устойчивость стенки подкрановой балки.
В стенке подкрановой балки возникают нормальные напряжения  , местные напряже-ния
, местные напряже-ния  и касательные напряжения
и касательные напряжения 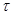 . От действия этих напряжений стенка может потерять устойчивость.
. От действия этих напряжений стенка может потерять устойчивость.
Условная гибкость стенки равна

Так как  то стенку подкрановой балки укрепляют поперечными ребрами жесткости. Шаг основных поперечных ребер жесткости “а” принимаем не более 2
то стенку подкрановой балки укрепляют поперечными ребрами жесткости. Шаг основных поперечных ребер жесткости “а” принимаем не более 2  , так как
, так как  т.е. а
т.е. а 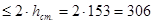 см
см
Принимаем а = 2 м
К нижнему поясу подкрановой балки в целях уменьшения концентрации напряжений в растянутой зоне ребра жесткости не доводят на 60 мм.
Ширина двух сторонних ребер принимается  мм принимаем 120 мм.
мм принимаем 120 мм.
Толщина ребра  мм
мм
Проверка устойчивости подкрановой балки проводится в двух отсеках ближе к середине пролета, где наибольший момент и ближе у опоре где наибольшая поперечная сила Q.

Рисунок 2.28
Вычисляем х1 и х2
 мм
мм
 мм
мм
Проверяем местную устойчивость стенки балки первого отсека. Расположение катков кранов и эпюры Q и М показаны на рис. 2.28. Опорная реакция равна
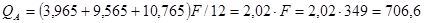 кН
кН
Средние значения изгибающего момента и поперечной силы на расстоянии х1 = 1,235 м от опоры (с учетом коэффициента  = 1,05 на массу тормозной балки) составляют:
= 1,05 на массу тормозной балки) составляют:
в сечении 1-1
 кН м
кН м
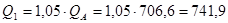 кН
кН
в середине отсека при х1 = 1,235 м
 кН м
кН м
 кН
кН
в сечении 2-2
 кН м
кН м
 кН
кН
Средние значения момента и поперечной силы в расчетной отсеке:
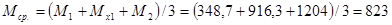 кН м
кН м
 кн
кн
Определяем напряжения в стенке опорного отсека при х1 = 1,235 м:
нормальные (в уровне верхней кромки стенки)
 кН/см2
кН/см2
касательные напряжения
 кН/см2
кН/см2
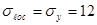 кН/см2, т.к.
кН/см2, т.к.  , а
, а  , то
, то
Критические напряжения. По формуле 81 /3/
 кН/см2 /3 форм. 75/
кН/см2 /3 форм. 75/
где с2 – коэффициент, определяемый по /3 табл. 25/ т.к. 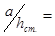 200 / 153 = 1,3, что > 0,8 с2 = 49
200 / 153 = 1,3, что > 0,8 с2 = 49
 для определения
для определения  по форм. 80 /3/;
по форм. 80 /3/;  /3 табл. 22/
/3 табл. 22/
 /3 форм. 76/
/3 форм. 76/
где  - отношение большей стороны отсека к меньшей,
- отношение большей стороны отсека к меньшей, 
 кН/см2
кН/см2
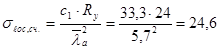 кН/см2
кН/см2
где с1 – коэффициент, принимаемый по /3 табл. 23/ в зависимости от отношения  и значения
и значения 

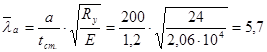
Проверяем устойчивость стенки балки по формуле 79 /3/
 (2.76)
(2.76)
где  = 1,1 по табл. 6 /3/
= 1,1 по табл. 6 /3/
 т.е.
т.е.
устойчивость стенки в опорном отсеке балки обеспечена.
Проверяем устойчивость стенки балки в среднем (третьем от конца) отсеке, середина которого расположена на расстоянии х2 = 5,235 м от опоры. Нагрузку от колеса крана Fк располагаем посередине длины расчетного отсека.
Вычисляем опорные реакции
 кН
кН
в сечении 3-3 Q равна

посередине отсека и в сечении 4-4 Q равна:

Среднее значение с учетом 
 кН
кН
Изгибающий момент равен (рис. 2.28)
 кН м
кН м
 кН м
кН м
 кН м
кН м
 кН
кН
Определяем напряжения в стенке среднего отсека:
нормальные
 кН/см2
кН/см2
касательные
 кН/см2
кН/см2
 кН/см2
кН/см2
т.к. 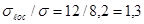 больше значений указанных в табл. 24 /3/, то
больше значений указанных в табл. 24 /3/, то  кН/см2 / 3 ф.75/
кН/см2 / 3 ф.75/
 ,
,  определено при х1 = 1235 мм, т.е. в первом отсеке.
определено при х1 = 1235 мм, т.е. в первом отсеке.
Проверяем устойчивость стенки среднего отсека балки:

т.е. устойчивость стенки в среднем отсеке балки обеспечена.
2.6.8 Расчет опорной часть подкрановой балки
Концы балки усиливаются торцевыми опорными поперечными ребрами, которые передают опорное давление с балки на колонну.
Требуемая площадь сечения ребра находится из условия сжатия
 (2.80)
(2.80)
где F – опорная реакция подкрановой балки F = Qmax
 cм2
cм2
По требуемой площади по сортаменту ГОСТ 82-70 принимаем размеры торцевого опорного ребра
 мм;
мм;  см2
см2
При этом необходимо убедится, что свес опорного ребра не требует местную устойчивость. Гибкость свеса  не должна превышать значений, установленных в /3 табл. 29*/, т.е.
не должна превышать значений, установленных в /3 табл. 29*/, т.е. 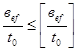 (2.81)
(2.81)
где 


Опорное ребро вместе с частью стенки шириной
 см может потерять устойчивость из плоскости балки как центрально сжатая сила F стойка высотой hсm с условной площадью
см может потерять устойчивость из плоскости балки как центрально сжатая сила F стойка высотой hсm с условной площадью
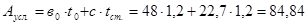 см2
см2
Проверка устойчивости производится по формуле
 (2.82)
(2.82)
где  - коэффициент продольного изгиба, определяемый по гибкости условной стойки по /3 табл. 72/, равной
- коэффициент продольного изгиба, определяемый по гибкости условной стойки по /3 табл. 72/, равной
 (2.83)
(2.83)
где iст. – радиус инерции условной стойки,  ,
,
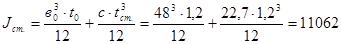 см4
см4
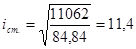 см
см

 кН/см2 < 26,4
кН/см2 < 26,4
Опорное ребро приваривается к балке угловыми швами. Рассчитываем вертикальные швы, длина которых 
Исходя из этого определяем требуемый катет шва:
-по металлу шва
 см
см
- по металлу границы сплавления
 см
см
Прикрепление опорного ребра к стенке балки производим полуавтоматической сварной проволокой Св-08ГА.
По табл. 34 /3/  ;
; 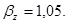 По табл. 3 /3/
По табл. 3 /3/  кН/см2
кН/см2
 кН/см2
кН/см2
 ,
,  мм /по табл. 38, 3/
мм /по табл. 38, 3/
 мм, принимаем kf = 8 мм
мм, принимаем kf = 8 мм
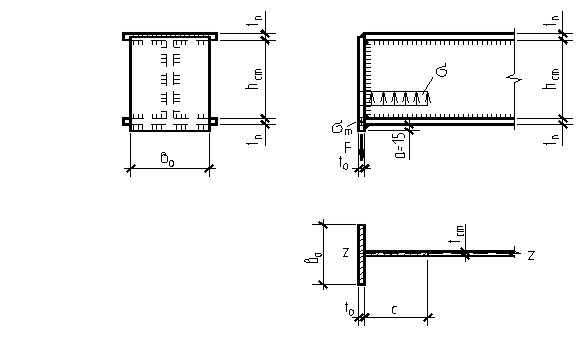
Рисунок 2.29 - Торцевое опорное ребро