II. Расчёт зубчатых колёс редуктора

I. Выбор электродвигателя и кинематический расчет

 

1.1. По табл. 1.1[2,с.5] примем:

КПД пары цилиндрических зубчатых колес h1 = 0,98; коэффициент, учитывающий потери пары подшипников клчеиия, h2 = 0,99; КПД открытой цепной передачи h3 = 0,92; КПД, учитывающий потери в опорах вала приводного барабана, h4 = 0,99.

Общий КПД привода

h = h1h2²h3h4 = 0,98 × 0,992 × 0,92 × 0,99 = 0,875

 

1.2. Мощность на валу барабана P б = F _л v л = 6 × 1,3 = 7,8 кВт.

1.3. Требуемая мощность электродвигателя

 

Ртр = = = 8,91 кВт.

 

1.4. Угловая скорость барабана

ωб = = = 6,5 с^-1.

 

1.5. Частота вращения барабана

 

п _б = = = 62 мин^-1.

1.6. Выбераем электродвигатель по таблице П.1 [2, с 390] по требуемой мощности. При этом, согласно рекомендации [2, с 36], примем i_p = 3÷6, а i_ц=3÷6. Тогда i_общ = i_p × i_ц = 9÷36. Выбираем электродвигатель трёхфазный коткозамкнутый серии 4А, закрытый, обдуваемый, с синхронной частотой вращения 1000 мин^-1, 4А 160 S6 УЗ, с параметрам Р_дв=11,0 кВт и скольжением 2,7%.

 

1.7. Номинальная частота вращения

 

п _дв = п _с (1 - ) = 1000 (1 - 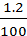) = 988 мин^-1.

 

ω_дв = с^-1.

 

 

1.8.

Лист             Изм. Лист № докум Подпись Дата

Проверим общее передаточное отношение

 

i =

 

1.9. Определим передаточное число цепной передачи исходя из расчёта, что u_p=5

 

u_ц =

 

Результаты расчётов сводим в таблицу

 

Вал В	п 1 = п дв =988 мин-1	ω1 = ωдв = 103.4с-1
Вал С	п 2 = = 198 мин-1	ω2 = c-1
Вал А	п б = 62 мин-1	ωб = 6,5 с-1

 

 

1.10. Определим вращающие моменты:

 

На валу шестерни

 

Т₁ = = = 86,2 10³ Н мм

 

На валу шестерни

 

Т₂ = Т₁ u_p = 86,2 10³ 5 = 431 10³ Н мм

 

На барабане

 

Т₃ = Т₂ u_ц = 431 10³ 3,2 = 1379,2 10³ Н мм

 

 

II. Расчёт зубчатых колёс редуктора

 

2.1. Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками [табл. 3.3]; для шестерни сталь 45, термическая обработка — улучшение, твердость

НВ 230; для колеса - сталь

Лист             Изм. Лист № докум Подпись Дата

45, термическая обработка - улучшение, но твердость на 30 единиц ниже - НВ 200.

Допускаемые контактные напряжения [2, формула (3.9)]

 

[σ_Н] = ,

где σ_НLmi_b – предел контактной выносливости при базовом исле циклов.

По табл. 3.2 [2,с.34] для углеродистых сталей с твердостью поверхностей

зубьев менее НВ 350 и термической обработкой (улучшением)

 

s_{Н lim b}=2 НВ + 70;

 

К_HL — коэффициент долговечности; при числе циклов нагружения больше базового, что имеет место при длительной эксплуатации редуктора, принимают К_HL=1; коэффициент безопасности [S_H]= 1,10.

 

Для косозубых колес расчетное допускаемое контактное напряжение по формуле (3.10) [2,с.45]

 

[s_Н] = 0,45 ([s_Н1] + [s_Н2]);

 

для шестерни [s_Н1] = = ≈ 482 МПа;

 

для колеса [s_Н2] = = ≈ 428 МПа;

 

Тогда расчётное допускаемое контактное напряжение

 

[s_Н] = 0,45 (482 + 428) = 410 Мпа.

 

Требуемое условие [s_Н] ≤ 1,23 [s_Н2].

 

2.2. Коэффициент КНb, несмотря на симметричное расположение колес относительно опор, примем выше рекомендуемого для этого случая, так как со стороны цепной передачи действуют силы, вызывающие дополнительную деформацию ведомого вала и ухудшающие контакт зубьев. Принимаем предварительно по табл. 3.1 [2, с.32], как в случае несимместричного расположения колес, значение КНb=1,25.

 

Принимаем для косозубых колес коэффициент ширины венца по межосевому расстоянию ψ_ba= 0.4 [2, с.36].

Межосевое расстояние из условия контактной выносливости активных

Лист             Изм. Лист № докум Подпись Дата

поверхностей зубьев по формуле [2, с.43]

 

а_w = K_a(u-1) 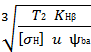= 43(5+1) 176.5 мм,

 

где для косозубых колёс К_а = 43, а передаточное число нашего редуктора u=u_p=5.

 

Ближайшее значение межосевого расстояния по ГОСТ 2185-66

а_w =200 мм [2, с.36].

 

2.3. Нормальный модуль зацепления принимаем по следующей рекомендации:

m_n=(0.01 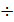0.02) a_w = (0.01 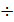0.02) 200 = 2 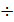4 мм;

принимаем по ГОСТ 9563-60* m_n=2,5 мм [2, с.36].

 

2.4. Принимаем предварительно угол наклона зубьев β=10 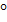и определим число зубьев шестерни и колеса:

 

z₁= 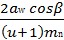= = 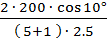= 26,2.

 

Принимаем z₁=26; тогда z₂ = z₁u = 26 = 130.

 

2.5. Уточнённое значение угла наклона зубьев

 

cosβ = 0.975;

 

cosβ=12 50`.

 

2.6. Основные размеры шестерни и колеса:

 

диаметры делительные:

d1= 66.66 мм;

d2= 333,34 мм;

 

Проверка a_w = = = 200 мм;

 

диаметры вершин зубьев:

Лист             Изм. Лист № докум Подпись Дата

 

d_a1= d₁ + 2m_n = 66,66 + 2 2,5 = 71,66 мм;

d_a2= d₂ + 2m_n = 333,34 + 2 2,5 = 338,34 мм;

 

ширина колеса b₂ = ψ_ba a_w = 0,4 200 = 80 мм;

ширина шестерни b₁ = b₂ + 5 мм = 85 мм.

 

2.7. Определяем коэффициент ширины шестерни по диаметру:

 

ψ_bd = = 1,275.

 

2.8. Окружная скорость колёс и степень точности передачи

м/с.

 

При такой скорости для косозубых колёс следует принять 8-ю степень точности [2, с.32].

 

2.9. Коэффициент нагрузки

К_Н = К_НβК_НαК_Нυ .

 

Значения К_Нβ даны в табл. 3.5[2, с.39]; при ψ_bd = 1,275, твёрдости НВ ≤ 350 и несимметричном расположении колёс относительно опор с учётом изгиба ведомого вала от натяжения цепной передачи К_Нβ 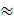1,155.

 

По табл. 3.4[2, с.39], при 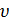= 3,38 м/с и 8-й степени точности К_Нα 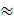1,08.

По табл. 3.6[2, с.40], для косозубых колёс при 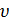≤ 5 м/с имеем = К_Нυ = 1,0.

Таким образом

К_Н = 1,04 1,09 1,0 = 1,134.

 

2.10. Проверка контактных напряжений

 

σ_Н = = = 310 МПа < [σ_Н] = 410 МПа.

 

2.11. Силы, действующие в зацеплении:

 

окружная F_t = = = 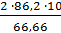2586 H.

радиальная F_r = F_t = 2586 = 971 H.

осевая F_a = F_t tgβ = 2586 0,221 = 571,506 H.

 

 

2.12. Проверяем зубья на выносливость по напряжения изгиба по формуле:

σ_F = ≤ [σ_F].

 

2.13. Здесь коэффициет нагрузки K_F=K_FβK_Fυ. По табл. 3.7 [2, с.43], при ψ_bd = 1,275, твёрдости НВ ≤ 350 и несиметричном расположении зубчатых колёс относительно опор K_Fβ = 1,30. По табл. 3.8 [2, с.43]. Таким образом, коэффициент K_F = 1,3 1,3 = 1,69;

 

2.14. Y_F – коэффициент, учитывающий фору зуба и зависящий от эквивалнтного числа зубьев z_υ:

 

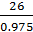
у шестерни z_υ1 = = 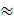28;

у колеса z_υ2 = = 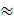140;

 

Y_F1 = 3,84 и Y_F2 = 3,60 [2, с.42].

 

2.15. Допускаемое напряжение по формуле [2, с.43]

 

[σ_F] =

 

По табл. 3.9. [2, с.44] для стали 45 улучшенной при твёрдости НВ ≤ 350 _{lim b} = 1.8НВ.

Для шестерни _{lim b} = 1.8 230 = 415 МПа; для колеса _{lim b} = 1.8 200 = 360 МПа; [S_F] = [S_F]` [S<sub>F</sub>]`` - коэффициент безопасности, где [S<sub>F</sub>]`=1,75. [S_F]``=1. Следовательно, [S_F]=1,75.

 

Допускаемое напряжения:

 

для шестерни [σ_F1]

Лист             Изм. Лист № докум Подпись Дата

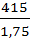= = 237 МПа;

для колеса [σ_F2] = = 206 МПа;

 

2.16. Находим отношение :

 

для шестерни = 62 МПа;

для колеса = 57,5 МПа;

Дальнейший расчет следует вести для зубьев колеса, для которого найденное отношение меньше.

 

2.17. Определяем коэффициенты Y_β и K_Fα:

 

Y_β

Лист             Изм. Лист № докум Подпись Дата

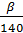= 1 - = 1 - 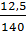= 1 – 0,09 = 0,91;

 

K_Fα = = = 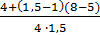0,92,

где для средних значений коэффициента торцоогоперекрытия ε_α = 1,5 и 8-й степени точности K_Fα = 0,92.

 

2.18. Проверяем прочность колеса зуба по формуле:

 

σ_F2 = ≤ [σ_F];

 

σ_{F2 =} = 66 МПа < [σ_F2] = 206 МПа.

 

Условие прочности выполнено.