Доказательства свойств определителя

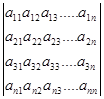= det A = det A^T

det A = det A^T

Выберем любое слагаемое из суммы определителя.

a_1i a_2j … a_nk

a_i1 a_j2 … a_kn  сумме det A^T

Следовательно определители равны.

Свойство №2: Если один из столбцов (строк) состоит из нулей, то определитель равен нулю.

Доказательство:

Пусть дана матрица, один столбец которой равен 0.

=detA подсчитаем определитель данной матрицы.

Подсчитаем определитель данной матрицы, используя правило равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям.

=0*а₂₂*а₃₃+а₁₂*а₂₃*0+а₃₂*а₁₃*0 = 0

=-(а₁₃*а₂₂*0+а₁₂*а₃₃*0+а₂₃*а₃₂*0)=0

Свойство доказано.

Свойство №3: Если один из определителей получен из другого определителя перестановкой двух столбцов (строк), то определители отличаются друг от друга знаком.

Доказательство: Возьмём матрицу определитель которой равен detA и переставим в ней 2 столбца. Получим:

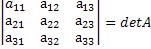, после перестановки получим: .

Посчитаем определители обеих матриц. Получим:

det A=(-1)⁰*((a₁₁*a₂₂*a₃₃+a₁₂*a₂₃*a₃₁+a₂₁*a₃₂*a₁₃)-(a₁₃*a₂₂*a₃₁+a₂₁*a₁₂*a₃₃+a₃₂*a₂₃*a₁₁))

det B=(-1)²*((a₃₁*a₂₂*a₁₃+a₂₁*a₁₂*a₃₃+a₃₂*a₂₃*a₁₁)-(a₃₃*a₂₂*a₁₁+a₁₂*a₂₃*a₃₁+a₂₁*a₃₂*a₁₃))

(a₁₁*a₂₂*a₃₃+a₁₂*a₂₃*a₃₁+a₂₁*a₃₂*a₁₃)-(a₁₃*a₂₂*a₃₁+a₂₁*a₁₂*a₃₃+a₃₂*a₂₃*a₁₁) +(a₃₁*a₂₂*a₁₃+a₂₁*a₁₂*a₃₃+a₃₂*a₂₃*a₁₁)-(a₃₃*a₂₂*a₁₁+a₁₂*a₂₃*a₃₁+a₂₁*a₃₂*a₁₃)=0

Получили, что det A=-det B.

Свойство доказано.

Свойство №4: Если все элементы какого-либо i-го столбца (строки) определителя являются суммами двух слагаемых, то такой определитель равен сумме двух определителей в первом из которых в качестве i-го столбца (строки) взяты первые слагаемые, а во втором – вторые слагаемые; при этом элементы всех остальных строк (столбцов) у каждого из трёх определителей одинаковы.

Доказательство:

Возьмём матрицу, в которой элементы первого столбца равны a_ij+b_j и посчитаем её определитель.

.

 

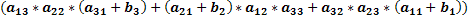Раскроем скобки и приведём подобные слагаемые.

 

.

То есть: .

 

Свойство доказано.

Свойство №5: Определитель, содержащий два пропорциональных, в частности два равных, столбца (строки), равен нулю.

Доказательство:

Пусть дан определитель detA≠0, содержащий две равные строки.

 

= detA; =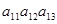

 

Поменяем местами эти равные строки. Получим новый определитель.

 

.

 

Так как данный определитель получен из определителя detA перестановкой строк, то из предыдущего свойства следует, что полученный определитель принимает значение –detA. В то же время, количество слагаемых и модуль значений определителей detA и –detA равны, то справедливо будет равенство detA=-detA. Из данного равенства следует что detA=0. Свойство доказано.

Свойство №6: Определитель не меняется, если к какому-нибудь столбцу (строке) прибавить линейную комбинацию других столбцов (строк).

Доказательство:

Возьмём матрицу коэффициентов и посчитаем её определитель.

 

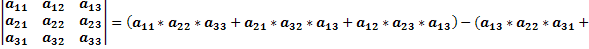
Прибавим к первому столбцу третий. Получим новую матрицу.

 

.

 

Посчитаем её определитель.

 

.

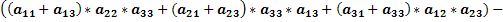
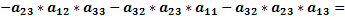
Свойство №7: Если все элементы какого-нибудь столбца (строки) определителя умножить на некоторое число k, то есть весь определитель умножается на k, то общий множитель любой строки или любого столбца можно выносить за знак определителя.

Доказательство: Возьмём матрицу и посчитаем её определитель.

 

То есть.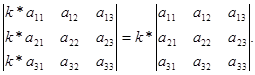

 

Свойство доказано.

 

 

5. Пример применения правила Крамера для решения систем n уравнений с n неизвестными

Определители очень широко используются при решении и исследовании систем линейных n уравнений с n неизвестными. Правило решения такой системы с помощью определителей называется правилом Крамера. Покажем это правило на примере.

Правило Крамера: правило решения системы n линейных уравнений. с n неизвестными, определитель которой отличен от нуля, всегда имеет решение. Это решение единственное и определяется таким правилом Крамера: значение каждого из неизвестных , где - определитель системы., матрица которого составлена из коэффициентов при неизвестных системы, а _I – определитель, матрица которого получена заменой столбца коэффициентов при данном неизвестном на столбец свободных членов системы. В случае если определитель системы равен нулю, система имеет бесконечно много решений.

Пусть дана система из трех уравнений с тремя неизвестными:

 

 

Посчитаем определитель матрицы системы, составленной из коэффициентов при неизвестных:

 

После подсчета определителя системы, подсчитаем определители неизвестных. Для этого вырезаем из столбец данной переменной, а на его место ставим столбец свободного члена.

 

= = = 6 = 6 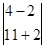= 6*(4*2-(-2)*11)=180

 

Согласно правилу Крамера значение неизвестной переменной равно частному от определителя данной неизвестной и определителя системы. Значит переменная x_{1= ;} x₁= .

Действуя по тому же алгоритму, найдем значения переменных x₂ и x₃:

По правилу равнобедренных треугольников, основания которых параллельны главной и побочной диагоналям матрицы получим:

 

= 2*11*4+3*11*(-1)+4*(-2)*3= 88-33-24=31 =60

-2*(-2)*11-3*4*4 – (-1)*11*3= 44-48+33=29

Значит x₂=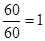

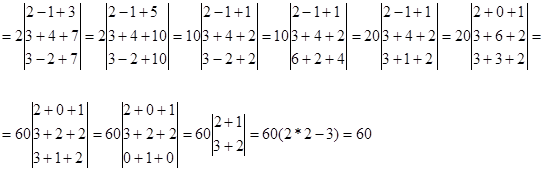
Значит x₃=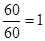

 

Для доказательства истинности правила Крамера, проверим полученные значения переменных, подставив полученные значения в систему:

 

 

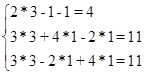
После подстановки мы получили верное числовое равенство, значит, правило Крамера истинно для решения системы n уравнений с n неизвестными. Ответ: (3;1;1)

Глава 2.Векторное произведение

Определения

Опр. Векторным произведением двух векторов А и В называется новый вектор С длина которого численно равна площади параллелограмма построенного на векторах А и В перпендикулярный к плоскости этих векторов и направленный в такую сторону, чтобы кратчайший поворот от А к В вокруг полученного вектора С представляется происходящим против часовой стрелки, если смотреть из конца С.

Из этого определения следует, что длина вектора С равна: .

Следствие. Векторное произведение равно нулевому вектору в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым, или если эти векторы параллельны (коллинеарны).