Расчётно-графическая работа
по учебной дисциплине «Статистика»
Модуль 1 Теория статистики
Вариант № 2
Выполнила
Выполнила: студентка группы ДЭ-500 Пономарева Е.А.
Шифр 092434622
Проверил: Яковенко Л.И.
Дата- ____________
Новосибирск 2016
Оглавление
Задача 1. 3
Задача 2. 11
Задача 3. 21
Задача 4. 24
Задача 5. 30
Задача 6. 34
Список используемой литературы и источников: 41
Задача 1
В приложении Априведены данные о выручке (нетто) от продажи товаров, продукции, работ, услуг (без НДС, акцизов и других аналогичных платежей) микропредприятий одной из отраслей экономики региона. Используя таблицу случайных чисел [1] или их генератор, включенный в различные статистические (математические) пакеты программ обработки данных на ПЭВМ, сформируйте массив случайных чисел и произведите 30-процентную простую случайную бесповторную выборку.
По выборочным данным:
1) постройте интервальный ряд распределения, образовав четыре группы с равными интервалами, представьте его в табличной и графической форме; по сгруппированным данным определите аналитическим и графическим методами модальное и медианное значение изучаемого признака;
2) исчислите средний размер выручки от продажи товаров, продукции, работ, услуг одного микропредприятия, а также долю микропредприятий с размером выручки более 20 млн руб.;
3) с вероятностью 0,954 определите доверительные интервалы, в которых можно ожидать генеральные параметры: а) средний размер выручки от продажи товаров, продукции, работ, услуг одного микропредприятия; б) долю микропредприятий с размером выручки более 20 млн руб.; в) общий размер выручки от продажи товаров, продукции, работ, услуг микропредприятий региона; г) число микропредприятий с размером выручки более 20 млн руб.
Подтвердите достоверность полученных оценок расчетом генеральных характеристик.
Сделайте выводы.
Решение:
Таблица № 1 – Результаты 30- процентной случайной бесповторной выборки (данные выбраны с помощью генератора случайных чисел)
| № предприятия | Выручка, млн. руб. | № предприятия | Выручка, млн. руб. | № предприятия | Выручка, млн. руб. |
1) Построить интервальный ряд распределения, образовав четыре группы с равными интервалами.
Размер интервала рассчитывается по формуле:
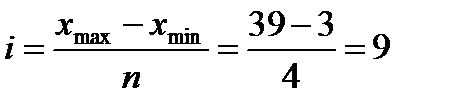млн. руб.
где: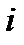 
– величина интервала;
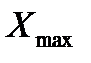– максимальное значение 
;
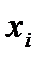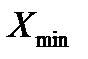– минимальное значение ;
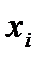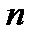– число интервалов.
Таблица 2 – Распределение предприятий по группам и определенной границы интервала:
| Группы предприятий по размеру выручки от реализации, млн. руб | Число предприятий | % от общего количества | Средняя выручка, млн. руб |
| до 11, 0 | 26,7 | 7,63 | |
| 11,1 - 20,0 | 33,3 | 15,9 | |
| 20,1 - 29,0 | 26,7 | 25,38 | |
| 29,1 - 39,0 | 13,3 | 35,0 | |
| Итого: | 18,77 |
Для расчета средней выручки по группам, нужно использовать формулу арифметической простой:
,
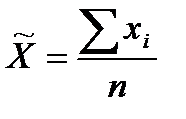где: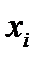 
- годовой размер выручки от продажи товаров, продукции, работ, услуг одного предприятия i-тых малых предприятий;
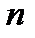- объём выборки.
В группе предприятий с выручкой от 29,9 до 39,0 млн. руб. средняя выручка составит: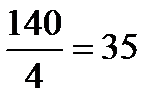 
млн. руб.
Аналогично будет и с остальными группами.
Вывод: средний размер выручки от продажи товаров, продукции, работ, услуг, составляет 20,98 млн. руб.
Таблица 3 – Рабочая таблица для расчета средней выручки
| Группы по размерам выручки, млн. руб | № предприятия | Выручка, млн. руб |
| до 11,0 | ||
| Итого: | ||
| 11,1 - 20,0 | ||
| Итого: | ||
| 20,1 - 29,0 | ||
| Итого: | ||
| 29,1 - 38,0 | ||
| Итого: |
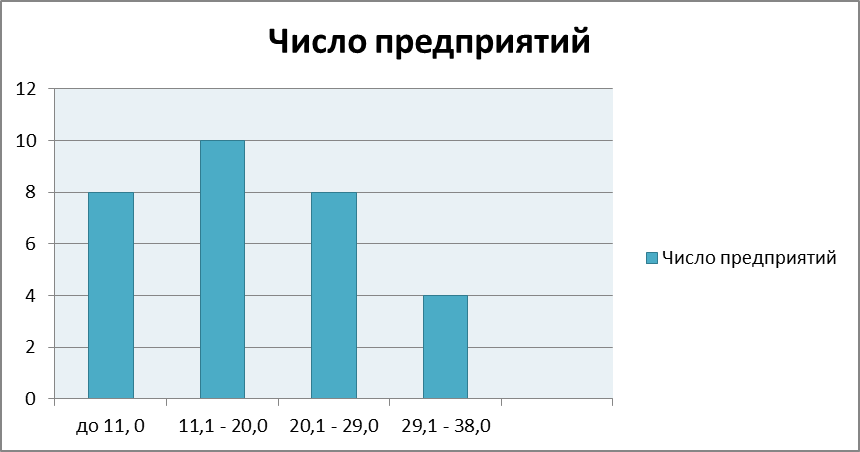
Данный график свидетельствует о том, что с повышением размера выручки предприятия, численность предприятий падает.
2) Вычислим средний размер выручки от продажи товаров, продукции, работ, услуг одного предприятия, а также долю малых предприятий с размером выручки более 20 млн. руб
Таблица 4 -Перераспределение на 2 группы с выручкой до 19 млн. руб. и более 20 млн. руб.
| Группы по размеру выручки, млн. руб | Число предприятий | % от общего количества | Средний размер выручки, млн. руб |
| до 19 | 60,0 | 11,78 | |
| 20 и более | 40,0 | 27,0 | |
| Итого: | 100,0 | 18,77 |
Средний размер выручки от продажи товаров одного предприятия:
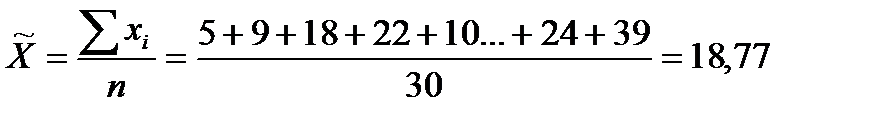млн. руб
Доля микропредприятий с размером выручки более 20 млн. руб составит: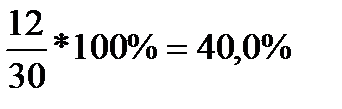 
Вывод: количество предприятий с размером выручки более 20 млн. руб. составляет 40% от общего числа предприятий.
3) С вероятностью 0,954 определим доверительные интервалы, в которых можно ожидать генеральные параметры:
а) Доверительные интервалы для среднего размера выручки рассчитываются по формуле:
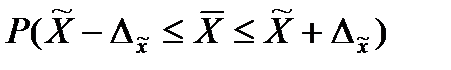= 0,954,
Предельная ошибка выборки для средней определяется по формуле:
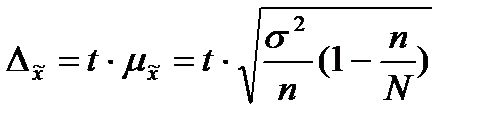; где:
- среднеквадратичная ошибка в выборочной характеристике (для простого бесповторного случайного отбора)
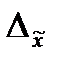- предельная ошибка;
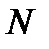=100 (общее число малых предприятий региона)
P = 0,954
t = 2
Дисперсия: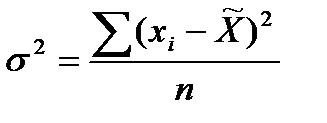 
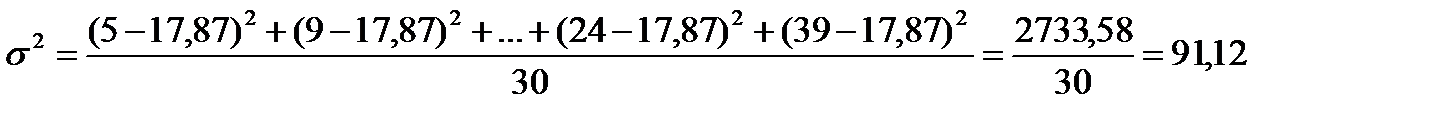(млн.руб.)
Предельная ошибка выборки для средней:
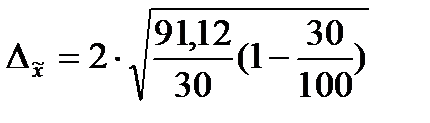= 2,92 (млн.руб),
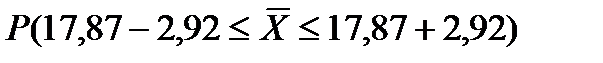= 0,954,
= 0,954,
Средний размер выручки по генеральной совокупности составляет:
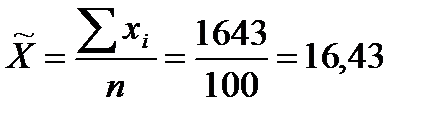млн.руб
Фактический средний размер выручки по генеральной совокупности по всем предприятиям составляет 16,43 млн. руб., что входит в доверительный интервал.
б) пределы для доли:
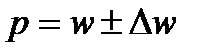
Предельная ошибка для доли:
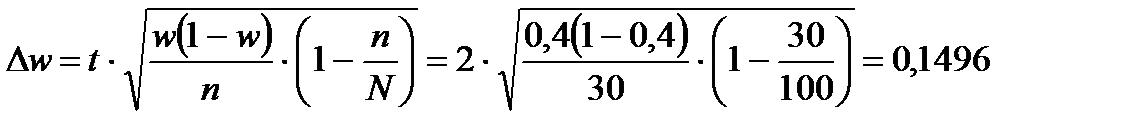
Пределы для доли:
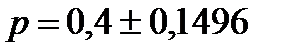
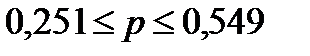
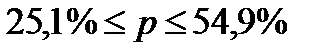
Доля предприятий в генеральной совокупности с объемом выручки более 20 млн. руб по 100 предприятиям составляет 33,3%, что входит в доверительный интервал.
в) общая выручка малых предприятий региона:
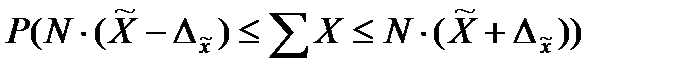= 0,954,
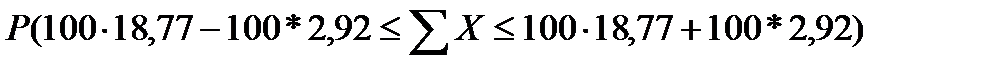= 0,954,
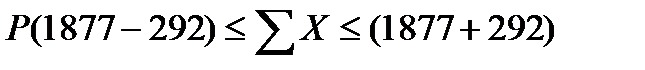= 0,954,
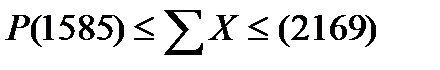
т.е. общая выручка генеральной совокупности колеблется в пределах от 1585 млн. руб. до 2169 млн. руб.
Общий размер выручки по генеральной совокупности составляет 1643 млн.руб. что входит в доверительный интервал.
г) число предприятий с объемом выручки более 20 млн. руб.:
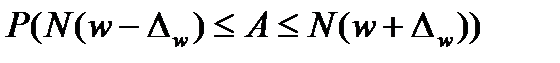= 0,954,
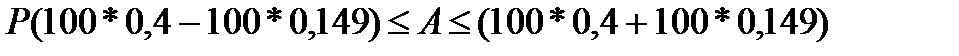= 0,954,
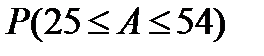= 0,954,
Число предприятий с объемом выручки более 20 млн. руб. в генеральной совокупности колеблется в пределах от 25 единиц до 54 единиц.
Фактическое число предприятий в генеральной совокупности с объемом выручки более 20 млн. руб. составляет 34, что входит в доверительный интервал.
Задача 2
Используя статистическую информацию, размещенную в сети Интернет на официальном сайте Федеральной службы государственной статистики или официальных публикациях Росстата (режим удаленного доступа https://www.gks.ru), постройте временной ряд за последние 8 – 10 лет по любому из заинтересовавших Вас показателей (с мотивацией обоснования выбора). Проанализируйте данные. Для этого:
1) определите все возможные цепные, базисные и средние показатели анализа ряда динамики;
2) произведите сглаживание уровней временного ряда методами укрупнения интервалов, скользящей средней, а также аналитического выравнивания (интервал укрупнения и период скольжения определите самостоятельно).
3) осуществите аналитическое выравнивание уровней анализируемого динамического ряда, проведите на его основе экстраполяцию показателя на среднесрочную длину прогнозного горизонта (2-3 года).
Для визуализации анализируемых, расчетных и прогнозируемых данных используйте табличный и графический методы.
Сделайте выводы.
Решение:
Я выбрала показатель численности населения, т.к. меня интересует то, как изменялось население в течение этого времени. Имеется ряд динамики по численности населения за 2006-2015 гг. (Оценка на первое января Всероссийской переписи населения)
| Годы | Численность населения, млн. чел. | |
| 143,2 | ||
| 142,8 | ||
| 142,8 | ||
| 142,7 | ||
| 142,8 | ||
| 142,9 | ||
| 143,0 | ||
| 143,3 | ||
| 143,7 | ||
| 146,3 | ||
| И с т о ч н и к: режим удаленного доступа: https://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/population/demography/# |
1) цепные, базисные и средние показатели анализа ряда динамики:
В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными.
Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным. Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.
Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста.
Темп роста есть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные.
Темп прироста есть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель).
Цепные показатели
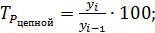
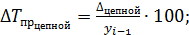
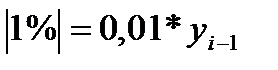
Таблица 5 – Расчет цепных показателей
| Год | Численность населения, млн.чел. | Цепные показатели динамики | |||
| Абсолютный прирост, млн. чел. | Темп роста, % | Темп прироста, % | Абсолютное значение 1% прироста, млн. чел. | ||
| 143,2 | … | … | … | … | |
| 142,8 | -0,4 | 99,7 | -0,3 | 1,43 | |
| 142,8 | 100,0 | 1,43 | |||
| 142,7 | -0,1 | 99,9 | -0,1 | 1,43 | |
| 142,8 | 0,1 | 100,1 | 0,1 | 1,43 | |
| 142,9 | 0,1 | 100,1 | 0,1 | 1,43 | |
| 0,1 | 100,1 | 0,1 | 1,43 | ||
| 143,3 | 0,3 | 100,2 | 0,2 | 1,43 | |
| 143,7 | 0,4 | 100,3 | 0,3 | 1,44 | |
| 146,3 | 2,6 | 101,8 | 1,8 | 1,46 |
Базисные показатели
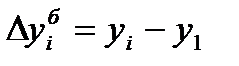
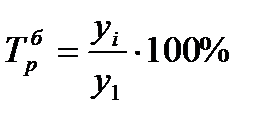
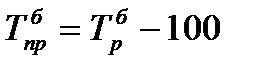
Таблица 6 – Расчет базисных показателей
| Год | Численность населения, тыс.чел. | Базисные показатели динамики | ||
| Абсолютный прирост, тыс. чел. | Темп роста, % | Темп прироста, % | ||
| 143,2 | …… | 100,0 | ||
| 142,8 | -0,4 | 100,3 | -0,3 | |
| 142,8 | -0,4 | 100,0 | ||
| 142,7 | -0,5 | 100,1 | -0,1 | |
| 142,8 | -0,4 | 99,9 | 0,1 | |
| 142,9 | -0,3 | 99,9 | 0,1 | |
| -0,2 | 99,9 | 0,1 | ||
| 143,3 | 0,1 | 99,8 | 0,2 | |
| 143,7 | 0,5 | 99,7 | 0,3 | |
| 146,3 | 2,6 | 101,8 | 1,8 |
Для того, чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за этот же промежуток времени:
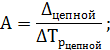
Средние показатели
Средние по рядам динамики:
По интервальному динамическому ряду из абсолютных величин с равными интервалами, как в нашем случае, средний уровень ряда определяется по средней арифметической простой из уровней ряда:
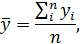
где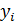 
- уровни ряда для i-го периода;
n – число уровней в ряду динамики.
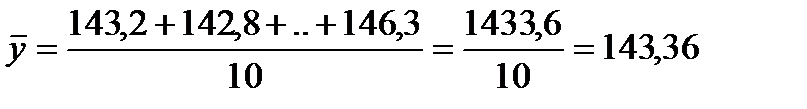млн. чел.
В среднем в каждом году в Российской Федерации число населения составляло 143 млн. чел.
Среднегодовые показатели
o средний абсолютный прирост
Средний абсолютный прирост определяется как средняя арифметическая простая из цепных приростов:
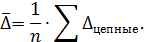
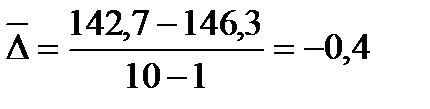млн. чел.
Население ежегодно в период 2006-2009 гг. в среднем уменьшалось на 4 тыс. человек.
o средний темп роста
Для обобщения характеристики интенсивности роста рассчитывается средний темп (коэффициент) роста по средней геометрической простой:
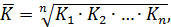
Где:
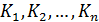– цепные коэффициенты роста;
n – число цепных коэффициентов роста.
Kp =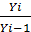 
(цепной)
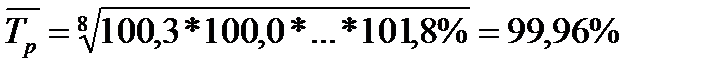
Соответственно мы понимаем, что средний темп роста составит 99,96 %.
o средний темп прироста
Среднегодовой темп прироста определяется на основе среднего темпа роста:
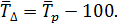
По данным таблицы среднегодовой темп роста составит:
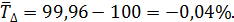
Средние показатели динамики, которые мы рассмотрели, достаточно широко используются при экстраполяции тенденции ввиду их простоты и возможности четко интерпретировать результат
2)Проведем сглаживание уровней временного ряда различными методами:
Метод укрупнения интервалов. В соответствии с ним ряд динамики разделяют на некоторое достаточно большое число равных интервалов; если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов). В нашем случае разбиваем ряд динамики на 5 интервалов по 2 года.
| Годы | Численность населения, млн. чел. | Численность населения, млн. чел | Показатель средней численности населения за год, млн. чел |
| 143,2 | |||
| 142,8 | |||
| 142,8 | 285,5 | 142,8 | |
| 142,7 | 142,8 | ||
| 142,8 | 285,7 | 142,9 | |
| 142,9 | 142,9 | ||
| 286,3 | 143,2 | ||
| 143,3 | 143,2 | ||
| 143,7 | |||
| 146,3 |
Метод скользящей средней. Аналитическое выравнивание уровней динамического ряда не дает хороших результатов при прогнозировании, если уровни ряда имеют резкие периодические колебания. В этих случаях простым путем определения тенденции развития явления представляется сглаживание динамического ряда методом скользящих средних.
Чтобы заменить фактические уровни временного ряда скользящими средними, выбирается период сглаживания. Чаще рекомендуется нечетный период скольжения: 3, 5, 7, 9. Соответственно рассчитываются 3-, 5-, 7- и 9-членная скользящие средние.
Так как скользящая средняя относится к середине интервала, за которой она рассчитана, то динамический ряд сглаженных уровней сокращается на (n-1) уровень при нечетном периоде скольжения и на n уровней – при четном периоде скольжения.
Результаты сглаживания по методу скользящих средней.
Период скольжения – 3 года,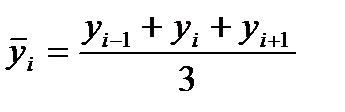 
| Годы | Численность населения, млн. чел. | Сглаженные уровни | |
| Простая скользящая средняя | |||
| 3-членная | 5-членная | ||
| 143,2 | - | - | |
| 142,8 | 142,9 | - | |
| 142,8 | 142,8 | 142,9 | |
| 142,7 | 142,8 | 142,8 | |
| 142,8 | 142,8 | 142,9 | |
| 142,9 | 142,9 | 142,9 | |
| 143,1 | 143,1 | ||
| 143,3 | 143,1 | 143,8 | |
| 143,7 | 144,4 | - | |
| 146,3 | - | - |
Как видно из таблицы, трехчленная скользящая средняя демонстрирует выровненный динамический ряд с разнонаправленной тенденцией движения уровней: снижение численности до 2009 г., затем увеличение до 2015 года. Чтобы исправить это нарушение закономерности, можно попытаться увеличить период скольжения до 5. Однако в нашем примере увеличение периода скольжения не дало положительных результатов.
Простые скользящие средние в ряде случаем позволяют выявить тенденцию лишь в общих чертах, ибо при сглаживании исчезают изгибы линии тенденции и некоторые уровни показывают вместо спада, имевшего место реально, подъем или наоборот.
Метод аналитического выравнивания. При наличии тенденции в ряду динамики его уровни можно рассматривать как функцию времени (t) и случайной компоненты (ε). Тогда модель уравнения динамического ряда выразим в виде:
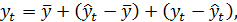
где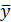 
- средний уровень динамического ряда (является теоретическим уровнем при отсутствии тенденций);
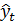- теоретический уровень временного ряда, связанный с действием основной тенденции развития.
В этой модели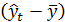 
представляет собой эффект тенденции, а 
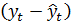- случайную составляющую ε. Так как 
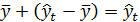, данную модель моно представить следующим образом:
Совершенно ясно, что практическая значимость модели будет выше, чем будут остаточные колебания 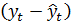. Следовательно, результаты прогноза зависят от принятой математической функции выравнивания, т.е. от типа тренда.
В настоящее время компьютерные программы анализа временных рядов предлагают достаточно широкий набор математических функций для построения уравнения тренда. Наиболее часто используются полиномы К -й степени, экспоненты, различного рода кривые с насыщением.
В общем виде полином К -й степени представляет собой выражение:
При К =1 получаем линейный тренд:
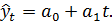
По содержанию линейный тренд означает, что уровни динамического ряда изменяются с одинаковой скоростью. В этом можно убедиться, если в уравнение линейного тренда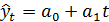 
подставить порядковые значения t:
| Годы | Численность населения, млн. чел | Расчеты графы | ||||||
| y | t |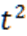 
| y*t |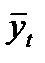 
| 
| 
| ||
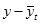
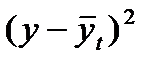
| 143,2 | 143,2 | 142,77 | 0,43 | 0,1849 | ||||
| 142,8 | 285,6 | 142,84 | -0,04 | 0,0016 | ||||
| 142,8 | 428,4 | 142,91 | -0,11 | 0,0121 | ||||
| 142,7 | 570,8 | 142,98 | -0,28 | 0,0784 | ||||
| 142,8 | 143,05 | -0,25 | 0,0625 | |||||
| 142,9 | 857,4 | 143,12 | -0,22 | 0,0484 | ||||
| 143,19 | -0,19 | 0,0361 | ||||||
| 143,3 | 1146,4 | 143,26 | 0,04 | 0,0016 | ||||
| 143,7 | 1293,3 | 143,59 | 0,11 | 0,0121 | ||||
| 146,3 | 146,04 | 0,26 | 0,0676 | |||||
| Итого: | 1433,5 | 7903,1 | - | 0,5053 |
По итоговым данным определяем параметры уравнения:
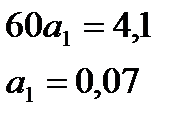
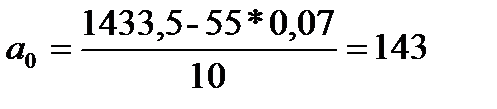
В результате получаем следующее уравнение основной тенденции численности населения в Российской Федерации за 2006-20015 гг.: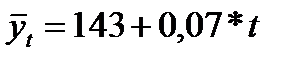 
Вывод: При помощи различных методов сглаживания уровней временного ряда была установлена тенденция к снижению численности населения в Российской Федерации за 2006-2009 гг, а затем увеличение численности до 2015 г.
Задача 3
На отчетную дату имеются данные по микрорайону города (данные условные).
| Номер дома | Число этажей в доме | Общая площадь дома, м2 | Процент жилой площади в доме | Процент жилой площади, требующей ремонта | Среднее число жителей на одном этаже, чел. |
Определите средние значения по каждому признаку. Постройте исходные соотношение (логические основы) каждой средней величины. Напишите формулы расчета, введя условные буквенные обозначения компонентов средней.
Укажите виды использованных средних величин. Сделайте выводы.
Решение:
v Среднее число этажей в доме обозначим и определим по формуле средней арифметической простой:
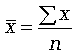
Исходное соотношение:
ИСС =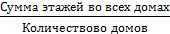 
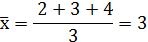
где x- отдельные значения варьирующего признака;
n – число единиц совокупности.
v Средняя общая площадь одного дома вычислим по формуле:
,
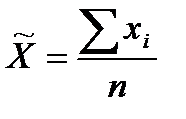Исходное соотношение:
ИСС = 
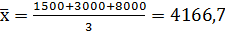м2
v Удельный вес жилой площади в % найдем по формуле относительной величины структуры:
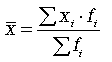
Исходное соотношение:
ИС =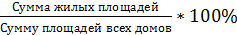 
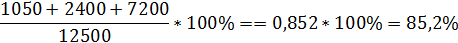
1) 1500*0,7= 1050 (м2)
2) 3000*0,8=2400 (м2)
3) 8000*0,9=7200 (м2)
v Средний процент жилой площади, требующей ремонта обозначим и определим по формуле средней арифметической взвешенной:
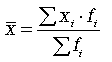
Исходное соотношение:
ИСС = 
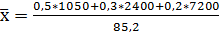=32%
х – это процент жилой площади, требующей ремонта;
f – процент жилой площади в доме.
v Среднее число жильцов на этаж вычислим, используя формулу:
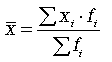
Исходная величина:
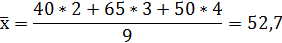
| Номер дома | Число этажей в доме | Общая площадь дома, м2 | Процент жилой площади в доме, % | Процент жилой площади, требующей ремонта,% | Среднее число жителей на одном этаже, чел. |
| Итого | 85,2 |
Вывод: Судя по данным мы узнаём, что на отчетную дату по микрорайону города, в доме, где проживают в среднем около 500 человек, необходим ремонт 32% жилой площади, остальная же площадь соответствует нормам проживания.
Задача 4
По данным опроса руководителей малых предприятий добывающих и обрабатывающих производств России в 2005 г. получены оценки основных факторов, ограничивающих рост производства в сферах экономической деятельности (в процентах от числа опрошенных):
| Факторы, ограничивающие рост производства | Вид экономической деятельности | |
| добыча полезных ископаемых | обрабатывающие производства | |
| Недостаточный спрос на продукцию предприятия на внутреннем рынке | ||
| Недостаточный спрос на продукцию предприятия на внешнем рынке | ||
| Конкурирующий импорт | ||
| Высокий уровень налогообложения | ||
| Изношенность и отсутствие оборудования | ||
| Неопределенность экономической ситуации | ||
| Высокий процент коммерческого кредита | ||
| Недостаток финансовых средств | ||
| Недостаток квалифицированных рабочих | ||
| Отсутствие или несовершенство нормативно-правовой базы | ||
| Нет ограничений | ||
| Источник: Малое предпринимательство в России. 2006: Стат.сб./Росстат. - М., 2006. - С. 89. |
Определите, в какой мере согласуются мнения руководителей малых предприятий различных сфер экономической деятельности относительно факторов, ограничивающих рост производства. Оценку осуществите с помощью коэффициентов ранговой корреляции Ч. Спирмэна и М. Кендэла.
Сделайте выводы.
Решение:
Коэффициент ранговой корреляцииСпирмена - непараметрический метод, который используется с целью статистического изучения связи между явлениями. В таком случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Практический расчет коэффициента ранговой корреляции Спирмена включает этапы:
1) Сопоставить каждому из признаков их порядковый номер (ранг) по возрастанию (или убыванию).
2) Определить разности рангов каждой пары сопоставляемых значений.
3) Возвести в квадрат каждую разность, и суммировать полученные результаты.
4) Вычислить коэффициент корреляции рангов по формуле:
,
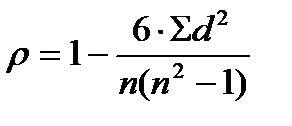Где:
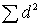- сумма квадратов разностей рангов, а 
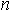- число парных наблюдений.
d – Разность рангов признаков Х и У;
n – Число наблюдаемых единиц.
При использовании коэффициента ранговой корреляции условно оценивают тесноту связи между признаками, считая значения коэффициента равные 0,3 и менее, показателями слабой тесноты связи; значения более 0,4, но менее 0,7 - показателями умеренной тесноты связи, а значения 0,7 и более - показателями высокой тесноты связи.
Для удобства вычисления коэффициента можно составить такую таблицу:
| Факторы, ограничивающие рост производства | Rх | Rу | d=Rх - Rу | d2 |
| -4 | ||||
| -5 | ||||
| -8 | ||||
| Итого: |
В нашем случае получим:
,
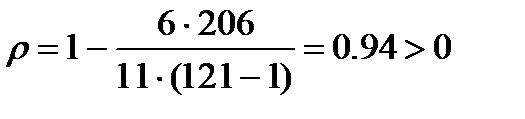Вывод: относительно факторов, ограничивающих рост производства, существует прямая высокая тесная связь между мнениями руководителей малых предприятий различных сфер экономической деятельности.
Коэффициент ранговой корреляции М. Кендалла является альтернативой методу определения корреляции Спирмана, ведь он предназначен для определения взаимосвязи между двумя ранговыми переменными.
Интерпретация результатов определяется как разность вероятностей совпадения и инверсии в рангах.
Для одних и тех же значений переменных значения коэффициента корреляции Спирмена будет всегда немного больше, чем значения коэффициента ранговой корреляции Кендалла, тогда как уровень значимости будет одинаков или же у коэффициента корреляции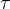 
-Кендалла будет немного больше.
Формула определения коэффициента ранговой корреляции может быть выражена следующим образом:
,
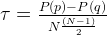где P(p) — число совпадений, P(q) — число инверсий, N — объем выборки
При наличии связанных рангов формула изменяется с учетом поправки на связанные ранги:
,
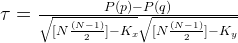где P(p) — число совпадений, P(q) — число инверсий, N — объем выборки,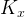 
— поправка на связи рангов переменной X, 
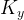— поправка на связи рангов переменной Y.
В упрощенном виде формулу коэффициента корреляции Кендалла можно записать как:
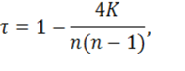,где
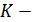статистика Кендэла (число инверсий).
Для определения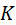 
необходимо:
1)ранжировать объекты по одной переменной в порядке возрастания рангов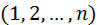 
2)определить соответствующие им ранги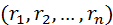 
по другой переменной.
Статистика 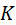равна общему числу инверсий (нарушений порядка, когда большее число стоит слева от меньшего) в ранговой последовательности (ранжировке) 
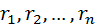. При полном совпадении двух ранжировок получим 
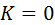и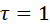 
; при полной противоположности можно показать, что 
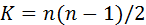и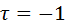 
. Во всех остальных случаях 
.
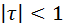| Факторы, ограничивающие рост производства | Rx | Ry | Числ |