Тема: Основні поняття та закони бульової алгебри. Логічні функції бульового базису. Поняття логічного елементу.
Цель: Ознакомиться с основными понятиями. Изучить основные функции, тождества и законы алгебры логики.
План:
1. Основные понятия и законы булевой алгебры
2. Логические функции булевого базиса:
o Логическая функция И.
o Логическая функция ИЛИ.
o Логическая функция НЕ.
3. Понятие логического элемента.
Ход лекции
1) Любое цифровое электронное устройство в процессе работы выполняет определенную последовательность операций, которую формируют на основе математической теории, созданной в 1848 году ирландским ученым Дж. Булем и известной под названием алгебра логики или Булева алгебра.
Высказывание это такое предложение, которое может соответствовать действительности, а может не соответствовать. В первом случае его называют истинным (1), в другом – ложным (0). В алгебре логики высказывание является переменной, которая может иметь одно из двух возможных значений и над которой можно выполнять действия.
По смыслу высказывания делят на простые и сложные. Если высказывание содержит одно какое-либо замечание, сообщение или утверждение, то его называют простым.
Используя высказывания и их логические значения, можно анализировать работу электрических схем.
| Обозначим высказывание «выключатель включен» через х, а высказывание «лампочка светит» через у. |
| + – |
| Е |
| SA |
| HL |
Если выключатель включен, т.е., х =1, в цепи проходит электрический ток и лампа горит, значит, у =1.
Если выключен, то высказывание х ошибочно (х =0), т.к. у =0.
Таким образом, можно составить цепочку логических рассуждений:
|
х = 1 ® у = 1
х = 0 ® у = 0
Алгебра логики оперирует с переменными, которые принимают два значения: истины и не истины, т.е. 0 или 1. Такая переменная называются двоичными аргументами и обозначают Х; они могут быть связаны между собой различными логическими операциями (лог. сложением, лог. умножением и т.д.). Логическая функция может быть представлена различным числом логических операций над двоичными аргументами.
Логические функции, представляющие одну логическую операцию, называются элементарными или основными логическими функциями. Логическая функция f (х1, х2,…,хn) также как и х1×х2×х3×…хn, от которых она зависит, может принимать значение либо 0, либо1.
Основные законы алгебры логики
| № п/п | Законы | Математическая запись |
| Идемпотентные (Тавтологии) | Х × Х = Х; Х + Х = Х | |
| Переместительные (коммутативные) | Х1 + Х2 =Х2 + Х1; Х1 · Х2 = Х2 · Х1 | |
| Сочетательные (Ассоциативные) | (Х1 + Х2) + Х3 = Х1 + (Х2 + Х3) (Х1 · Х2) · Х3 = Х1 · (Х2 · Х3) | |
| Распределительные (Дистрибутивные) | (Х1 + Х2) · Х3 = Х1 · Х3 + Х2 · Х3 (Х1 · Х2) + Х3 = (Х1 + Х3) · (Х2 + Х3) | |
| Законы отрицания | Х +  = 1; Х × = 1; Х ×  = 0;
Х + 0 = Х; Х + 1 = 1;
Х × 1 = Х; Х × 0 = 0 = 0;
Х + 0 = Х; Х + 1 = 1;
Х × 1 = Х; Х × 0 = 0
| |
| Двойного отрицания | 
| |
| Двойственности (теоремы де Моргана) | 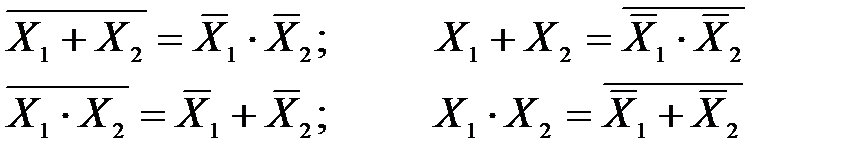
| |
| Поглощения |  ; x + A × x = x; ; x + A × x = x;

 × X2 + X1 = X1 + X2
( × X2 + X1 = X1 + X2
( + X2) × X1 = X1 × X2 + X2) × X1 = X1 × X2
| |
| Операции склеивания | 
 x × A +
x × A +  × A = A × A = A
|
Основные тождества алгебры логики
| № п/п | Аксиома |
| 1. | x = 0, если x ¹ 1; x = 1, если x ¹ 0. |
| 2. | 1 V 1 = 1; 0 V 0 = 0 |
| 3. | 0 ∙ 0 = 0; 1 ∙ 1 = 1 |
| 4. | 0 V 1 = 1 V 0 = 1; 1 ∙ 0 = 0 ∙ 1 = 0 |
| 5. |  = 1; = 1;  = 0 = 0
|
2) Логическая функция И называется конъюнкцией и выполняет операцию логического умножения, (×, L, &):
у = х1 × х2 = х1 L х2 = х1 & х2 = х1 х2;
f (х1, х2,…,хn) = х1×х2×х3×…хn
Функция И равна 1 только при равенстве всех аргументов 1, т.е., если х1=1, х2=1, хn=1. Значения аргументов и функции записывают в таблицу, которая называется таблицей истинности. Для логической функции с n количеством входных переменных получается 2 n входных комбинаций, т.е. двухэлементная функция имеет четыре входные комбинации, а трехэлементная – восемь и т.д. Часто операцию И называют операцией логического умножения (т.к. таблица истинности данной операции аналогична таблице умножения 0 и 1).
| х1 | х2 | y = х1×х2 |
Логическая функция ИЛИ называется дизъюнкцией и выполняет операцию логического сложения, (+,V,1):
у = х1 V х2;
f (х1, х2,…,хn) = х1Vх2Vх3V…хn.
Функция ИЛИ равна 1, если хотя бы один из аргументов х1, или х2, или хn равен 1. Выражение у будет ложным только тогда, когда оба высказывания х1 и х2 будут ложны. Часто операцию ИЛИ называют логической суммой (т.к. первые три соотношения таблицы аналогичны сложению двух чисел).
| х1 | х2 | y = х1V х2 |
Логическая функция НЕ называется инверсией и выполняет функцию логического отрицания  (– знак инверсии).
(– знак инверсии).
Функция НЕ равна 1, если аргумент равен 0.
| х | 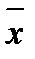
|
Логические элементы – это элементарные схемы, электронные модели логических функций. Соединяя эти схемы-модели между собой по определенным алгоритмам, можно построить цифровые устройства любой сложности.
Простейшие цифровые элементы должны выполнять три элементарные логические операции (сложения, умножения и отрицания), к которым можно свести любую др. операцию. Пример: ИЛИ, И, НЕ, И-НЕ, ИЛИ-НЕ.
В зависимости от технологии изготовления ИС подразделяются на серии (семейства), различающиеся физическими параметрами базовых элементов, а также числом и функциональным назначением входящих в их состав микросхем. Под серией понимают совокупность типов ИС, которые могут выполнять различные функции, имеют единое конструктивно-технологическое исполнение и предназначены для совместного применения. В настоящее время разработано несколько десятков технологий изготовления ИС.
Наиболее широкое распространение получили микросхемы транзисторно-транзисторной логики (ТТЛ), эмиттерно-связанные интегральные логические элементы (ЭСЛ) и схемы на МОП (металл – окисел – полупроводник) – структурах.
Каждая технология непрерывно совершенствуется с целью увеличения быстродействия ИС, уменьшения потребляемой мощности и увеличения степени интеграции — числа элементов, размещенных на кристалле заданной площади.
Логический элемент И
| Х1 |
| Х2 |
| Х1 ∙ Х2 |
| & |
Логический элемент, выполняющий конъюнкцию, называют логическим элементом И (конъюнктор). Логический элемент И дает на выходе напряжение только тогда, когда на все его входы подается напряжение: х1=1; х2=1 → у=1, в других случаях у=0.
| + |
| – |
| Х1 |
| Х2 |
| Y |
| E |
| HL |
Логический элемент ИЛИ
Функцию дизъюнкции выполняет логический элемент ИЛИ (дизъюнктор).
| – |
| + |
| X1 |
| X2 |
| E |
| HL |
| Y |
| Х1 |
| Х2 |
| Х1 Ú Х2 |
Результат работы логического элементаИЛИ – появление выходного напряжения тогда, когда U подано хотя бы на один из входов, т.е. х1=0, х1=0→у=0, в остальных случаях у=1.
Логический элемент НЕ
Логическую функцию НЕ выполняет логический элемент НЕ.
| Х |
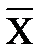
|
Логический элемент НЕ имеет один вход и один выход.
Если на входе есть напряжение, которое соответствует лог. 1, то на выходе напряжение соответствует лог. 0., и наоборот, т.е. х=1→у=0; х=0→у=1.
| Y |

|
| E |
| + |
| – |
| R |
Если выключатель разомкнут, т.е. х=0, то через лампу идет ток и к ней будет приложено V(y=1), лампа горит.
Если выключатель замкнут (х=1), то ток пройдет через контакты выключателя и на лампе V не будет (у=0), лампа не горит.
Если выходы одних элементов соединить со входами других, то получим схему, реализующую более сложную функцию.
Совокупность различных типов элементов, достаточных для воспроизведения любой логической функции, называется логическим базисом.
Элементы И, НЕ представляют такой базис. Элемент типа ИЛИ может быть получен соединением И и НЕ.

|
| X1 |
| X2 |
| X1 |
| X2 |
| & |
| X1·X2 |
| Y |
| Y |
| X1 |
| X2 |
Элементы И, ИЛИ, НЕ называются одноступенчатыми, т.к. они реализуют одну логическую функцию.
Контрольные вопросы.
1. Что называется высказыванием?
2. Дайте определение логической функции
3. Перечислите основные логические операции.
4. Что называют таблицей истинности?
5. Перечислите основные тождества алгебры логики.
6. Дайте определение логического базиса.
Литература:
1. Калабеков Б.А., Мамзелев И.А. Цифровые устройства и МПС, - М.: Радио и связь, 1987. Стр. 95-106.
2. Евреинов Э.В., Цифровая и вычислительная техника, - М.: Радио и связь, 1991. Стр. 39-53.
3. Васильев В.И., Гусев Ю.М. Электронные промышленные устройства, - М.: Высшая школа, 1988. Стр. 63-73.
4. Пухальский Г.И., Новосельцева Т.Я. Проектирование дискретных устройств на интегральных микросхемах, -М.: Радио и связь, 1990. Стр. 5-7.