Величины, характеризующие колебательное движение.

КУРСОВАЯ РАБОТА

по учебной дисциплине “Физика”

на тему “Колебания и волны. Оптика. Квантовая и ядерная физика”

 

 

Выполнил студент

3 курса, гр. 6211У______________________________________

(подпись)

 

Проверил______________________________________________А.Б.Федоров

(оценка, подпись)

 

Глазов 2011

 

 

СОДЕРЖАНИЕ

 

ВВЕДЕНИЕ…………………………………………………………………………..3

1. Механические электромагнитные колебания. Гармонический осциллятор…..5

2. Корпускулярно-волновой дуализм в микромире. Гипотеза де - Бройля.

Некоторые свойства волн де - Бройля. Вероятностный смысл волн де –

Бройля………………………………..……………………………………………..8

3. Колебания………………………………………………..…..….……...………..10

4. Электромагнитные волны….. ……………………………………..……...…….11

5. Интерференция света …………………………………………...….…...…...….12

6. Дифракция света ……………………………………………………...............…14

7. Поляризация...………………………………………...………………………….15

8. Квантовая природа излучения……………….………………….…………...….16

9. Основные понятия квантовой механики …....…………………….…….……..18

10. Основные понятия квантовой механики ………………….………………….19

11. Квантовая физика. Строение атома ……………..............................................20

12. Ядерная физика ………...……………………...………………….….………...21

Заключение..……………………………………………………….………………..22

Литература……………………………………………..………………….………...23

Приложения……………………………………………………………………..….24

 

ВВЕДЕНИЕ

В курсовой работе охвачены вопросы разделов «Колебания и волны. Оптика» и «Квантовая и ядерная физика».

Задачи на гармонические колебания охватывают такие вопросы, как определение амплитуды скорости, ускорения, энергии, периода механических колебаний, силы тока, напряжения, энергии и частоты электромагнитных колебаний.

Волновые процессы представлены задачами, в которых определяются частота, длина, скорость распространения, энергия и объемная плотность энергии механических и электромагнитных волн.

Задачи по теме «Интерференция света» включают расчет интерференционной картины от двух когерентных источников, интерференцию в тонких пленках, полосы равной толщины и равного наклона.

Тема «Дифракция света» представлена задачами на определение количества зон Френеля, дифракции в параллельных лучах на одной щели, на плоской и пространственной дифракционных решетках, разрешающей способности дифракционной решетки.

Задачи по теме «Поляризация света» охватывают такие вопросы, как применение законов Брюстера, Малюса, определение степени поляризации, вращение плоскости поляризации в растворах и кристаллах.

Тема «Распространение света в веществе» включают законы теплового излучения, фотоэффект, эффект Комптона, давление света.

Изучение элементов атомной и ядерной физики начинается с элементов квантовой механики и рассмотрения таких вопросов, как корпускулярно-волновой дуализм материи, гипотезы де Бройля, что движение любой частицы согласно этой гипотезе всегда сопровождается волновым процессом. Исходя из соотношений неопределенностей Гейзенберга, определяются границы применимости классической механики и, что из этих соотношений вытекает необходимость описания состояния микрочастиц с помощью волновой функции.

При изучении элементов физики атомного ядра и элементарных частиц, рассматривается состав атомного ядра и его характеристики: масса, линейные размеры, момент импульса, магнитный момент ядра, дефект массы ядра, энергия и удельная энергия связи ядра. Рассматривая состав ядра и взаимодействие нуклонов в ядре, выявляются свойства ядерных сил и их обменная природа.

При изучении темы «Ядерные реакции», нельзя забывать, что во всех ядерных реакциях выполняются законы сохранения: энергии, импульса, момента импульса, электрического заряда, числа нуклонов. Особое внимание уделяется реакциям синтеза легких и деления тяжелых ядер, вопросам ядерной энергетики и проблемам управления термоядерными реакциями.

В задачах данной темы рассматриваются следующие вопросы: определение длины волны де Бройля движущихся частиц, соотношения неопределенностей Гейзенберга, применение уравнения Шредингера для частицы, находящейся в одномерной потенциальной яме с бесконечно высокими стенками, рентгеновское излучение и закон Мозли, закон радиоактивного распада, определение дефекта массы, энергии связи и удельной энергии связи ядра, энергии ядерных реакций.

1. МЕХАНИЧЕСКИЕ ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР.

 

Колеба́ния — повторяющийся в той или иной степени во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку. Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии. Выделение разных видов колебаний зависит от подчёркиваемых свойств колеблющихся систем.

Различают следующие виды колебаний:

- По физической природе:

· Механические (звук, вибрация)

· Электромагнитные (свет, радиоволны, тепловые)

· Смешанного типа — комбинации вышеперечисленных

- По характеру взаимодействия с окружающей средой

· Вынужденные — колебания, протекающие в системе под влиянием внешнего периодического воздействия. Примеры: листья на деревьях, поднятие и опускание руки.

· Свободные (или собственные) — это колебания в системе под действием внутренних сил, после того как система выведена из состояния равновесия (в реальных условиях свободные колебания всегда затухающие). Ярким примером свободных колебания является колебания груза, прикреплённого к пружине, или груза, подвешенного на нити.

· Автоколебания — колебания, при которых система имеет запас потенциальной энергии, расходующейся на совершение колебаний (пример такой системы — механические часы).

· Параметрические — колебания, при которых за счет внешнего воздействия происходит изменение какого-либо параметра колебательной системы.

Величины, характеризующие колебательное движение.

· Амплитуда — максимальное отклонение колеблющейся величины от некоторого усреднённого её значения для системы, А (м)

· Период — промежуток времени, через который повторяются какие-либо показатели состояния системы (система совершает одно полное колебание), Т (сек)

· Частота — число колебаний в единицу времени, 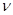(Гц, сек⁻¹).

Связь частоты и периода выражается формулой:

.

В круговых или циклических процессах вместо характеристики «частота» используется понятие круговая (циклическая) частота 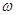(рад/сек, Гц, сек⁻¹), показывающая число колебаний за 2π единиц времени:

· Смещение — отклонение тела от положения равновесия, х (м).

· Фаза колебаний — определяет смещение в любой момент времени, то есть определяет состояние колебательной системы, (рад).

Гармонические колебания — колебания, при которых колеб­лющаяся величина изменяется со временем по закону синуса (косинуса). Гармонические колеба­ния величины х описываются уравнением типа

.

Гармонический осциллятор — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы , пропорциональной смещению х (согласно закону Гука):

где k — положительная константа, описывающая жёсткость системы.

Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами смещения), груз на пружине, торсионный маятник и акустические системы. Среди других аналогов гармонического осциллятора стоит выделить электрический гармонический осциллятор,представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор.

2. КОРПУСКУЛЯРНО-ВОЛНОВОЙ ДУАЛИЗМ В МИКРОМИРЕ.

ГИПОТЕЗА ДЕ - БРОЙЛЯ. НЕКОТОРЫЕ СВОЙСТВА ВОЛН ДЕ - БРОЙЛЯ. ВЕРОЯТНОСТНЫЙ СМЫСЛ ВОЛН ДЕ - БРОЙЛЯ.

Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Французский ученый Луи де Бройль выдвинул в 1923 году гипотезу об универсальности корпускулярно-волнового дуализма. Он утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия E и импульс p, а с другой стороны — волновые характеристики — частота и длина волны. Формула де Бройля устанавливает зависимость длины волны λ, связанной с движущейся частицей вещества, от импульса p частицы:

,

где m — масса частицы, v — ее скорость, h — постоянная Планка, c — скорость света. Волны, о которых идет речь, называются волнами де Бройля.