Фазовая скорость волн де Бройля свободной частицы

где ω = 2πν — циклическая частота, E — полная (релятивистская) энергия частицы, р — импульс частицы, m, v — её масса и скорость соответственно, λ — длина дебройлевской волны, k=  - волновое число. Фазовая скорость vфаз волны де Бройля больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).
- волновое число. Фазовая скорость vфаз волны де Бройля больше скорости света, но относится к числу величин, принципиально неспособных переносить информацию (является чисто математическим объектом).
Групповая скорость волны де Бройля u равна скорости частицы v:
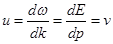 .
.
Следовательно, групповая скорость волн де Броля равна скорости частицы.
Волны де Бройля имеют специфическую природу, не имеющую аналогии среди волн, изучаемых в классической физике: квадрат модуля амплитуды волны де Бройля в данной точке является мерой вероятности того, что частица обнаруживается в этой точке. Дифракционные картины, которые наблюдаются в опытах, являются проявлением статистической закономерности, согласно которой частицы попадают в определенные места в приёмниках — туда, где интенсивность волны де Бройля оказывается наибольшей. Частицы не обнаруживаются в тех местах, где, согласно статистической интерпретации, квадрат модуля амплитуды «волны вероятности» обращается в нуль.
3.СВОБОДНЫЕ КОЛЕБАНИЯ
1. Материальная точка массой 7,1 г совершает гармонические колебания с амплитудой 2 см и частотой 5 Гц. Чему равна максимальная возвращающая сила и полная энергия колебаний?
| Дано: | СИ | Решение: |
 г
А=2 см г
А=2 см
 Гц Гц
|  кг кг
 м м
|
 -уравнение гармонических колебаний (1) -уравнение гармонических колебаний (1)
 (2) (2)
 , ,  =0 =0
 (3) (3)

 (4)
Подставляя (4) в (3) получаем: (4)
Подставляя (4) в (3) получаем:
 W=Tкин+Ппотен= Tmax=Пmax
W=Tкин+Ппотен= Tmax=Пmax
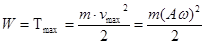

 H H
 Дж
Ответ: Дж
Ответ:  H; H;  Дж Дж
|
| Найти: Fmax W | Н Дж |
4.ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
2.В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,1 А/м. Определить амплитуду напряженности электрического поля волны и среднюю по времени плотность энергии волны.
| Дано: | СИ | Решение: |
Нm=0,1 А/м
 =1 =1

|
 -плотность потока энергии.
Так как величины Е и H в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение р равно: -плотность потока энергии.
Так как величины Е и H в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение р равно:
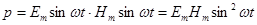 Учитывая, что в электромагнитной волне
Учитывая, что в электромагнитной волне
 , найдем: , найдем:
 ,
I= ,
I= 
 , ,
 B/м
I= B/м
I= 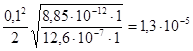 Вт/м2
Ответ: Вт/м2
Ответ:  B/м, I= B/м, I=  Вт/м2 Вт/м2
| |
| Найти: Еm I | B/м Вт/м2 |
5.ИНТЕРФЕРЕНЦИЯ СВЕТА
3. Расстояние между двумя когерентными источниками 0,9 мм, а расстояние от источников до экрана 1,5 м. Источники испускают монохроматический свет с длиной волны 0,6 мкм. Определить число интерференционных полос, приходящихся на 1 см экрана.
| Дано: | СИ | Решение: |




|  м м
 м м
 м м
|
 , где , где  - расстояние между двумя интерференционными максимумами. (1) - расстояние между двумя интерференционными максимумами. (1)
 - оптическая разность хода (2) - оптическая разность хода (2)
 
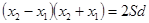 , (3) , (3)
 (4)
Подставляя в (3) (2) и (4) получим: (4)
Подставляя в (3) (2) и (4) получим:
 , ,  (5) (5)
 - условие интерференционного максимума, где - условие интерференционного максимума, где  . (6)
Подставляя в (6) (5) получим: . (6)
Подставляя в (6) (5) получим:
 (7)
Возьмем два соседних максимума k и k+1. (7)
Возьмем два соседних максимума k и k+1.
 (8)
Подставим (8) в (1) получим: (8)
Подставим (8) в (1) получим:
 , ,
 Ответ:
Ответ: 
|
Найти:

|
6.ДИФРАКЦИЯ СВЕТА
4. Параллельный пучок света от монохроматического источника ( = 0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром 1 мм. Темным или светлым будет центр дифракционной картины на экране, находящемся на расстоянии 0,5 м от диафрагмы?
= 0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром 1 мм. Темным или светлым будет центр дифракционной картины на экране, находящемся на расстоянии 0,5 м от диафрагмы?
| Дано: | СИ | Решение: |
 мм мм
 мкм мкм
 м м
|  м м
 м м
|
 , ,  , ,  - пренебрежимо мало, тогда - пренебрежимо мало, тогда  (1) (1)
 (2).
Подставим (2) в (1), получим (2).
Подставим (2) в (1), получим  .
Если m- четное, будет темное кольцо,
Если m – нечетное, будет светлое кольцо. .
Если m- четное, будет темное кольцо,
Если m – нечетное, будет светлое кольцо.
 Ответ:
Ответ:  , центр дифракционной картины на экране будет светлым. , центр дифракционной картины на экране будет светлым.
|
Найти:

|
7.ПОЛЯРИЗАЦИЯ
5. Под каким углом к горизонту должно находиться Солнце, чтобы его лучи, отраженные от поверхности воды, были максимально поляризованы?
| Дано: | СИ | Решение: |

|
 Пусть
Пусть  - угол падения солнечных лучей, - угол падения солнечных лучей,  - угол между направлением на Солнце и горизонтом.
По закону Брюстера - угол между направлением на Солнце и горизонтом.
По закону Брюстера 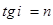 , где , где  - показатель преломления воды.
Тогда - показатель преломления воды.
Тогда  .
Тогда .
Тогда  Ответ:
Ответ: 
| |
Найти:

|
8.КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ
6. Определить максимальную скорость фотоэлектронов, вылетающих из вольфрамового электрода, освещаемого ультрафиолетовым светом с длиной волны 0,2 мкм.
| Дано: | СИ | Решение: |

 m=
m=  кг кг
| 
|
Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта:
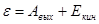 . .
 рассматривается как максимальная кинетическая энергия фотоэлектронов, а энергия фотона вычисляется по формуле: рассматривается как максимальная кинетическая энергия фотоэлектронов, а энергия фотона вычисляется по формуле:
 ,
где ,
где  - постоянная Планка; - постоянная Планка;  - скорость света в вакууме; - скорость света в вакууме;  - длина волны излучения. Подставляя числовые значения в первую формулу, получим, что энергия электромагнитного излучения - длина волны излучения. Подставляя числовые значения в первую формулу, получим, что энергия электромагнитного излучения  .
Так как энергия фотона .
Так как энергия фотона 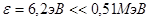 - меньше энергии покоя электрона, то данный случай является нерялетивистским, и при решении задачи максимальную кинетическую энергию фотоэлектрона определим по формуле - меньше энергии покоя электрона, то данный случай является нерялетивистским, и при решении задачи максимальную кинетическую энергию фотоэлектрона определим по формуле  .
Отсюда максимальная скорость фотоэлектронов будет равна .
Отсюда максимальная скорость фотоэлектронов будет равна  Подставляя числовые значения в полученную формулу находим
Подставляя числовые значения в полученную формулу находим   .
Ответ: .
Ответ:  
|
Найти:

|

|
9.ОСНОВНЫЕ ПОНЯТИЯ КВАНТОВОЙ МЕХАНИКИ
7. Какой кинетической энергией должен обладать электрон, чтобы дебройлевская длина волны была равна его комптоновской длине волны?
| Дано: | СИ | Решение: |
 кг кг

|
  де Бройля: де Бройля: 
 Комптона: Комптона:    умножаем ур-е на с: умножаем ур-е на с:
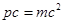 , где , где  - энергия покоя, тогда - энергия покоя, тогда 
 Из СТО: Из СТО: 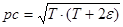 
 Решаем квадратное уравнение: D=8 Решаем квадратное уравнение: D=8 
 Так как
Так как  , то решением является только положительный корень: , то решением является только положительный корень:  , тогда , тогда  , подставим числовые значения , подставим числовые значения
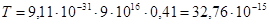 Дж: Дж: 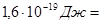 =
=  эВ
Ответ: эВ
Ответ:  эВ эВ
| |
Найти:

| эВ |
10.ОСНОВНЫЕ ПОНЯТИЯ КВАНТОВОЙ МЕХАНИКИ
8.Среднее расстояние электрона от ядра в невозбужденном атоме водорода равно 52,9 пм. Вычислить минимальную неопределенность скорости электрона в атоме.
| Дано: | СИ | Решение: |
 
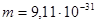 кг кг
|  м м
|
Применим соотношение неопределенностей к электрону, движущемуся в атоме водорода.  После подстановки числовых значений находим
После подстановки числовых значений находим   Ответ:
Ответ:  
|
Найти:

|

|
11.КВАНТОВАЯ ФИЗИКА. СТРОЕНИЕ АТОМА
9. Сколько линий спектра атома водорода попадает в видимую область ( = 0,40 — 0,76 мкм)? Вычислить длины волн этих линий. Каким цветам они соответствуют?
= 0,40 — 0,76 мкм)? Вычислить длины волн этих линий. Каким цветам они соответствуют?
| Дано: | СИ | Решение: |

|
Длины волн спектральных линий водорода всех серий определяются формулой 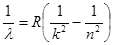 .
В видимой области спектра находятся первые четыре линии серии Бальмера (n=2, k=3,4,5,6). Длины волн этих линий будут равны: .
В видимой области спектра находятся первые четыре линии серии Бальмера (n=2, k=3,4,5,6). Длины волн этих линий будут равны:
 - красная линия - красная линия
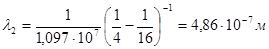 - голубая линия - голубая линия
 - фиолетовая линия - фиолетовая линия
 - фиолетовая линия
Ответ: - фиолетовая линия
Ответ:  , ,  , ,  , , 
| |
Найти:

| м |
12. ЯДЕРНАЯ ФИЗИКА
10.Вычислить дефект массы, энергию связи и удельную энергию связи дейтерия.
| Дано: | СИ | Решение: |

| Дефект массы ядра определяем по формуле
 .
Вычисление дефекта массы выполним во внесистемных единицах (а.е.м.). Для ядра .
Вычисление дефекта массы выполним во внесистемных единицах (а.е.м.). Для ядра   , ,  . Массы нейтральных атомов водорода и дейтерия, а также нейтрона найдем из таблицы.
Подставим найденные массы в выражение и произведем вычисления. В итоге получаем . Массы нейтральных атомов водорода и дейтерия, а также нейтрона найдем из таблицы.
Подставим найденные массы в выражение и произведем вычисления. В итоге получаем  а.е.м.
Энергия связи ядра определяется соотношением а.е.м.
Энергия связи ядра определяется соотношением  .
Энергию связи ядра также найдем во внесистемных единицах (МэВ). Для этого дефект массы подставим в выражение энергии связи в а.е.м., а коэффициент пропорциональности ( .
Энергию связи ядра также найдем во внесистемных единицах (МэВ). Для этого дефект массы подставим в выражение энергии связи в а.е.м., а коэффициент пропорциональности ( ) – в МэВ/(а.е.м.).
Подставляя числовые данные, получим ) – в МэВ/(а.е.м.).
Подставляя числовые данные, получим  МэВ.
Удельная энергия связи, приходящаяся на один нуклон МэВ.
Удельная энергия связи, приходящаяся на один нуклон  Подставляя числовые данные, получим
Подставляя числовые данные, получим  МэВ/нуклон
Ответ: МэВ/нуклон
Ответ:  а.е.м., а.е.м., 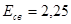 МэВ, МэВ,  МэВ/нуклон МэВ/нуклон
| |
Найти:



|
Заключение
В моей курсовой работе были рассмотрены следующие вопросы: механические гармонические колебания, гармонический осциллятор по теме «Свободные колебания» и корпускулярно-волновой дуализм в микромире, гипотеза де – Бройля, некоторые свойства волн де – Бройля, вероятностный смысл волн де – Бройля по теме «Основные понятия квантовой физики».
Решены задачи по следующим темам: «Свободные колебания», «Электромагнитные волны», «Интерференция света», «Дифракция света», «Волновая оптика», «Основные понятия квантовой механики», «Квантовая физика. Строение атома», «Ядерная физика».
Литература
1. Трофимова Т.Н. Курс физики.- М.: ВШ, 2000.
2. Савельев И.В. Курс общей физики,- М: Наука, 1982-1984, т. 1-3.
3. Сивухин Д.В. Общий курс физики. - М.: Наука, 1979-1989, т. I-V.
4. Огурцов А.Н. Лекции по физике.
5. Методические указания и контрольные задания для курсовой работы. –Г: 2007
Приложения
1. Основные физические постоянные (округленные значения)
| Физическая постоянная | Обозначение | Числовое значение |
| Нормальное ускорение свободного падения | g | 9,81 м/c2 |
| Гравитационная постоянная | G |  м3/(кг м3/(кг  с)2 с)2
|
| Постоянная Авогадро | N A |  моль-1 моль-1
|
| Молярная газовая постоянная | R | 8,31 Дж/(моль  К) К)
|
| Постоянная Больцмана | k |  Дж/К Дж/К
|
| Объем одного моля идеального газа при нормальных условиях (T 0 = 273,15 К, p 0 = 101325 Па) | V 0 |  м3/моль м3/моль
|
| Элементарный заряд | е |  Кл Кл
|
| Масса покоя электрона | m e |  кг кг
|
| Постоянная Фарадея | F | 9,65 Кл/моль |
| Скорость света в вакууме | с |  м/с м/с
|
| Постоянная Стефана — Больцмана | 
|  Вт/(м2 Вт/(м2  К4) К4)
|
| Постоянная Вина в первом законе (смещения) | b 1 |  м м  К К
|
| Постоянная Вина во втором законе | b 2 |  Вт/(м3 Вт/(м3  К5) К5)
|
| Постоянная Планка | h |  Дж Дж  с с
|

| 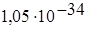 Дж Дж  с с
| |
| Постоянная Ридберга | R |  м-1 м-1
|
| Боровский радиус | r |  м м
|
| Комптоновская длина волны электрона | 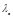
|  м м
|
| Энергия ионизации атома водорода | Е i |  Дж = 13,6 эВ Дж = 13,6 эВ
|
| Атомная единица массы | а. e. м. |  кг кг
|
| Энергия, соответствующая 1 а. е. м. | 931,50 МэВ | |
| Электрическая постоянная | 
|  Ф/м Ф/м
|
| Магнитная постоянная | 
|  Гн/м Гн/м
|
| Магнетон Бора | 
|  Дж/Тл Дж/Тл
|
| Ядерный магнетон | 
|  Дж/Тл Дж/Тл
|
2. Удельное сопротивление р, 10-8, Ом  м
м
| Вольфрам | 5,5 | Железо | 9,8 | Никелин | |
| Нихром | Медь | 1,7 | Серебро | 6,0 |
3. Показатель преломления
| Алмаз | 2,42 | Вода | 1,33 | Глицерин | 1,47 |
| Каменная соль | 1,54 | Кварц | 1,55 | Сероуглерод | 1,63 |
| Скипидар | 1,48 | Стекло | 1,52 | Кислород | 1,00027 |
4. Интервалы длин волн, соответствующие различным цветам спектра, нм
| Фиолетовый | 400 — 450 | Голубой | 480 — 500 | Желтый | 560 — 590 |
| Синий | 450 — 480 | Зеленый | 500 — 560 | Оранжевый | 590 — 620 |
| Красный | 620 — 760 |
5. Масса m 0 и энергия Е 0 покоя некоторых элементарных частиц и легких ядер
| Частицы | m 0 | Е 0 | ||
| а. е. м. | 10-27, кг | МэВ | 10-10, Дж | |
| Электрон | 5,486  10-4 10-4
| 0,00091 | 0,511 | 0,00081 |
| Протон | 1,00728 | 1,6724 | 938,23 | 1,50 |
| Нейтрон | 1,00867 | 1,6748 | 939,53 | 1,51 |
| Дейтрон | 2,01355 | 3,3325 | 1876,5 | 3,00 |
| a-частица | 4,0015 | 6,6444 | 3726,2 | 5,96 |
6. Множители и приставки для образования десятичных кратных и дольных единиц и их наименовании
| Приставка | множитель | Приставка | множитель | ||
| наименование | обозначение | наименование | обозначение | ||
| экса | Э | 1018 | санти | с | 10-2 |
| пета | П | 1015 | милли | м | 10-3 |
| тера | Т | 1012 | микро | мк | 10-6 |
| гига | Г | 109 | нано | н | 10-9 |
| мега | М | 106 | пико | п | 10-12 |
| кило | к | 103 | фемта | ф | 10-15 |
| деци | д | 102 | атто | а | 10-18 |
7. Работа выхода электронов из металла, эВ
| Алюминий | 3,7 | Литий | 2,3 | Платина | 6,3 | Цинк | 4,0 |
| Вольфрам | 4,5 | Медь | 4,4 | Цезий | 1,8 | Никель | 4,8 |
8. Элементы периодической системы н массы нейтральных атомов, а.е.м.
| Элемент системы | Изотоп | Масса | Элемент системы | Изотоп | Масса |
| Водород | — | Алюминий | 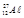
| 26,98135 | |

| 1,00783 | Кремний | 
| 26,81535 | |

| 2,01410 | Фосфор | 
| 32,97174 | |

| 3,01605 | Сера | 
| 32,97146 | |
| Гелий | — | Железо | 
| 55,94700 | |

| 3,01605 | Медь | 
| 63,5400 | |

| 4,00260 | Вольфрам | 
| 183,8500 | |
| Литий | 
| 7,01601 | Магний | 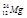
| 23,98504 |
| Бериллий | 
| 7,01169 | 
| 26,98436 | |
| Бор | 
| 10,01294 | Кальций | 
| 47,95236 |

| 11,00931 | Серебро | 
| 107,869 | |
| Азот | 
| 14,00307 | Радий | 
| 226,0254 |
| Кислород | 
| 15,99492 | Торий | 
| 232,038 |

| 16,99913 | Уран | 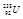
| 238,0508 |