Директрисы фигуры эллипс

Взаимное расположение прямых

Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.

1. Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны.

2. Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Пример

Даны y = 4x – 5 и y = –2x + 1
4x – 5 = –2x + 1
4x + 2x = 1 + 5
6x = 6
x = 1
y = 4 * 1 – 5 = –1 или y = –2 * 1 + 1 = –1

Таким образом точка пересечения (1; –1).

3. Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Эллипс (определ., урав-е., св-ва)

Эллипс - это геометрическая фигура, которая ограничена кривой, заданной уравнением .

Каноническое уравнение эллипса имеет вид , где 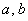– положительные действительные числа, причём .

Чертеж фигуры эллипс

F₁, F₂ – фокусы. F₁ = (c; 0); F ₂ (- c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема. Фокусное расстояние и полуоси связаны соотношением:

a² = b ² + c ².

Доказательство: В случае, если точка М находится на пересечении эллипса с вертикальной осью, r₁ + r₂ = 2* (по теореме Пифагора). В случае, если точка М находится на пересечении его с горизонтальной осью, r₁ + r ₂ = a – c + a + c. Т.к. по определению сумма r₁ + r ₂ – постоянная величина, то, приравнивая, получаем:

a ² = b ² + c ²

r₁ + r₂ = 2 a.

Эксцентриситет фигуры эллипс

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

е = с/ a.

Т.к. с < a, то е < 1.

Определение. Величина k = b / a называется коэффициентом сжатия, а величина 1 – k = (a – b)/ a называется сжатием.

Коэффициент сжатия и эксцентриситет связаны соотношением: k² = 1 – e ².

Если a = b (c = 0, e = 0, фокусы сливаются), то эллипс превращается в окружность.

Если для точки М(х ₁, у ₁) выполняется условие: , то она находится внутри эллипса, а если , то точка находится вне его.

Теорема. Для произвольной точки М(х, у), принадлежащей фигуре эллипс верны соотношения:

r ₁ = a – ex, r₂ = a + ex.

Доказательство. Выше было показано, что r₁ + r₂ = 2 a. Кроме того, из геометрических соображений можно записать:

После возведения в квадрат и приведения подобных слагаемых:

Аналогично доказывается, что r₂ = a + ex. Теорема доказана.

Директрисы фигуры эллипс

С фигурой эллипс связаны две прямые, называемые директрисами. Их уравнения:

x = a / e; x = - a / e.

Теорема. Для того, чтобы точка лежала на границе фигуры эллипс, необходимо и достаточно, чтобы отношение расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету е.

Пример. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину фигуры эллипс, заданного уравнением:

• Координаты нижней вершины: x = 0; y² = 16; y = -4.

• Координаты левого фокуса: c² = a ² – b² = 25 – 16 = 9; c = 3; F₂ (-3; 0).

• Уравнение прямой, проходящей через две точки:

Пример. Составить уравнение границы фигуры эллипс, если его фокусы F ₁ (0; 0), F₂ (1; 1), большая ось равна 2.

Уравнение границы имеет вид: . Расстояние между фокусами:

2 c = , таким образом, a² – b² = c² = 1/2

по условию 2а = 2, следовательно а = 1, b =

Итого искомое уравнение имеет вид: 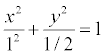.