Определение. Директрисами эллипса называются две прямые, которые в канонической для эллипса системе координат имеют уравнения
или 
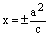. (13)
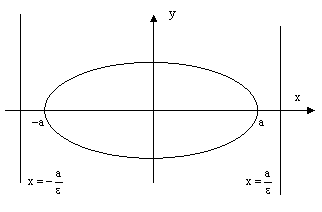
рис.8.
Теорема. Пусть М – произвольная точка эллипса,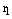 
, 
– ее фокальные радиусы, 
– расстояние от точки М до левой директрисы, 
– до правой. Тогда
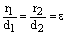, (14)
где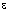 
– эксцентриситет эллипса.
Доказательство.
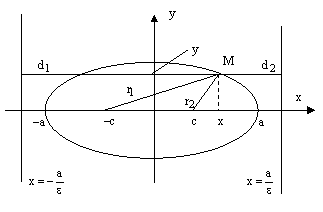
рис.9.
Пусть М(х, у) – координаты произвольной точки эллипса. Тогда
, 
,
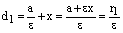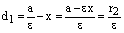откуда и следуют равенства (14).
Теорема доказана.
п.8. Фокальный параметр эллипса.
Определение. Фокальным параметром эллипса называется длина перпендикуляра, восстановленного в его фокусе до пересечения с эллипсом.
Фокальный параметр принято обозначать буквой р.
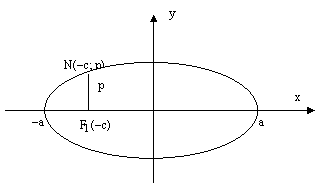
рис.9.
Из определения следует, что фокальный параметр
.
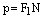Теорема. Фокальный параметр эллипса равен
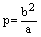. (15)
Доказательство. Так как точка N(–с; р) является точкой эллипса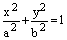 
, то ее координаты удовлетворяют его уравнению:
.
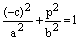Отсюда находим
,
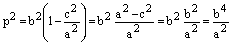откуда и следует (15).
Теорема доказана.
п.9. Второе определение эллипса.
Теорема из п.7. может служить определением эллипса.
Определение. Эллипсом называется ГМТ для которых отношениерасстояния до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой, есть величина постоянная меньше единицы и называемая его эксцентриситетом:
.
Определение. Директрисами гиперболы называются две прямые,уравнения которых в канонической для гиперболы системе координатимеют вид
.
Так как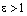 
, то 
.
Обозначение. Расстояние между директрисами обозначается 2d и равно
.
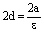рис.8.
Теорема. Для любой точки гиперболы отношение ее фокального радиуса к расстоянию до соответствующей директрисы есть величина постоянная равная эксцентриситету:
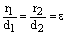. (7)
Доказательство. При выводе канонического уравнения гиперболы мы получили формулы для вычисления фокальных радиусов точки гиперболы с координатами М(х, у):
, 
,
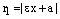где числа х, 
и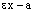 
имеют одинаковые знаки.
Из рисунка 8 мы видим, что при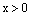 
, 
,
, 
,
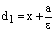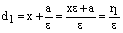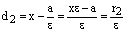откуда и следуют равенства (7). Аналогично доказываются формулы (7) и при 
.
Теорема доказана.
Пересечение прямой второго порядка и прямой
Классификация кривых второго порядка, приведение уравнения кривой второго порядка к каноническому виду.
Аффинные преобразования
При построении изображений часто приходится иметь дело с ситуациями, когда общее изображение (рисунок) включает в себя целый ряд компонент (подрисунков), отличающихся друг от друга только местоположением, ориентацией, масштабом, т.е. отдельные подрисунки обладают значительным геометрическим сходством.
В этом случае целесообразно описать один подрисунок в качестве базового, а затем получать остальные требуемые подрисунки путем использования операций преобразования.
С помощью операций преобразования можно выполнять следующие действия:
1) перемещать рисунки из одного места экрана в другое;
2) создавать рисунок из более мелких элементов (составных частей);
3) добавлять к существующему рисунку новые элементы;
4) увеличивать размер рисунка для улучшения его наглядности или отображения более мелких деталей;
5) уменьшать размер рисунка для внесения, например, поясняющих надписей или отображения на экране новых рисунков;
6) создавать движущиеся изображения.
Все изменения рисунков можно выполнить с помощью трех базовых операций:
1) переноса (перемещения) изображения;
2) масштабирования (увеличения или уменьшения размеров) изображения;
3) поворота изображения (употребляют также термины вращение, изменение ориентации).
Эти операции называются аффинными преобразованиями. Различают двумерные и трехмерные аффинные преобразования.
Основные геометрические свойства двумерных аффинных преобразований:
1) прямые линии после преобразований остаются прямыми;
2) параллельные прямые – параллельными;
3) Отношения деления отрезков остаются неизменными.
Основные геометрические свойства трехмерных аффинных преобразований:
1) плоскости после преобразования остаются плоскостями;
2) параллельные плоскости – параллельными.