Содержание домашнего задания. Выбор исходных данных
1. Начертить расчетную электрическую схему и записать исходные данные.
2. Рассчитать сопротивления реактивных элементов и записать в комплексной форме сопротивления ветвей схемы.
3. определить токи во всех ветвях схемы.
4. рассчитать и построить векторные диаграммы токов и напряжений.
5. Определить показания измерительных приборов.
6. рассчитать баланс мощностей и коэффициент мощности схемы.
Порядок выполнения расчетно-графической работы
1. Исходная электрическая схема домашнего задания приведена в приложении 1 (рис.П1). Числовые значения параметров схемы выбираются студентом из таблицы 3, приведенной в приложении 2. Номер варианта домашнего задания соответствует номеру, под которым студент записан в журнале у старосты группы.
2. Расчетно-графическая работа выполняется на листах А4 и, желательно, с использованием компьютера. Образец оформления титульного листа приведен в приложении 3.
3. Перед выполнением очередного пункта задания необходимо
написать заголовок и пояснить, что Вы собираетесь делать дальше.
При выполнении вычислений следует привести расчетную
формулу, подставить числовые значения всех величин,
входящих в формулу, и ответ с указанием единиц измерения в
системе СИ, затем конечные графики и векторные диаграммы в
соответствии с требованиями условия домашнего задания.
4. Используемые обозначения в формулах и на схемах должны соответствовать ГОСТу.
5. Работа над ошибками выполняется студентом с новой страницы, не
трогая уже проверенного преподавателем материала.
Следует написать заголовок «Работа над ошибками» и далее
выполнять работу над ошибками, заново приводя исправленные
рисунки, формулы и расчеты.
6. Срок сдачи второго домашнего задания – 10 неделя.
Методические указания
Расчет электрической цепи с использованием
Законов Кирхгофа
При расчете цепи переменного синусоидального тока можно воспользоваться законами Кирхгофа. Составить соответствующую систему уравнений можно либо для мгновенных значений токов и напряжений, либо в комплексной форме (см. табл.1).
Таблица 1
| 1-ый закон Кирхгофа | 2-ой закон Кирхгофа | |
| Для мгновенных значений | 
| 
|
| В комплексной форме | 
| 
|
Мгновенные значения токов и напряжений записываются в виде синусоидальных функций со своими начальными фазами 
и 
и 
.
Дальнейшие рассуждения будем проводить с использованием конкретной схемы (рис.1). Запишем систему уравнений по законам Кирхгофа для схемы рис.1 для мгновенных значений токов и напряжений:
.
Рис.1
Получили систему интегродифференциальных уравнений, записанных для синусоидально изменяющихся величин. Решать такую систему сложно.
Значительно удобнее решать систему уравнений, записанных с использованием комплексных величин.
Использование комплексного метода позволяет свести решение дифференциальных уравнений, записанных для мгновенных значений токов и напряжений, к решению алгебраических уравнений, записанных для комплексных величин.
|
Запишем систему уравнений для нашего примера с использованием комплексных величин. Предварительно перерисуем схему (рис.1), введя в нее новые обозначения, использующие комплексные величины (см. рис.2).
Рис.2
Закон Ома в комплексной форме для каждого из элементов схемы имеет вид: 
.
Здесь 
и 
- комплексные значения напряжения и тока на
участке цепи;
- комплексное сопротивление участка цепи,
которое в каждом конкретном случае
записывается согласно табл.2.
Таблица 2
|
Для составления системы уравнений по законам Кирхгофа необходимо предварительно задать положительные направления токов в ветвях схемы.
Первый закон Кирхгофа формулируется так:
Алгебраическая сумма комплексных значений токов в узле электрической цепи равна нулю.
.
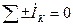Правило знаков: токи, направленные к узлу, берутся со знаком плюс, от узла – со знаком минус.
Количество уравнений, составляемое по первому закону Кирхгофа, на единицу меньше, чем число узлов в схеме.
Второй закон Кирхгофа формулируется так:
Алгебраическая сумма комплексных значений напряжений в замкнутом контуре равна алгебраической сумме комплексных значений э.д.с. в этом контуре
.
Правило знаков: выбираем направление обхода контура (по часовой стрелке или против). Если напряжение (или эдс) совпадает с направлением обхода контура, то берется со знаком плюс. Если напряжение (или эдс) направлено навстречу обходу контура, то берется со знаком минус.
Количество уравнений, составляемое по второму закону Кирхгофа, равно числу независимых контуров в схеме. Общее число уравнений, составленных по первому и второму законам Кирхгофа, должно равняться числу неизвестных (обычно – токов).
Система уравнений, записанная по законам Кирхгофа в комплексной форме для схемы (рис.2), будет
;
; (2)
.
Используя исходные данные, вычисляем все реактивные сопротивления: 
; 
; 
; 
,
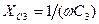где 
с-1, так как 
Гц.
Подставляем известные значения сопротивлений и напряжение источника 
в систему уравнений (2) и решаем ее. Получаем значения токов 
и, выбрав масштаб, строим векторную диаграмму токов на комплексной плоскости (рис.3).
|
Рис.3
Составление уравнения баланса мощностей
Для проверки правильности решения задачи в электротехнике обычно используют метод составления уравнения баланса мощностей. Комплексная мощность, отдаваемая источниками в электрическую цепь 
, должна быть равна комплексной мощности, потребляемой приемниками 
.
.
При этом должны выполняться раздельно равенства активных мощностей
и реактивных мощностей
.
Мощность источников рассчитываем в комплексной форме
.
Здесь для расчета комплексной мощности 
используется комплексно-сопряженное значение тока 
.
, 
, 
– полная, активная и реактивная мощности, измеряемые, соответственно, в ВА, Вт и ВАр.
Для приемников вычисляем раздельно активную мощность
и реактивную мощность
.
При выполнении реальных расчетов мощности источников и приемников могут несколько отличаться. Точность выполненного расчета схемы оценивают с помощью относительной погрешности при вычислении баланса активных мощностей
δР% = 
и реактивных мощностей
δQ% = 
.
При выполнении расчетов на компьютере эти погрешности не должны превышать 1%.