В системе (1) Коши компоненты деформации определяются тремя компонентами перемещений 
. Поэтому компоненты деформации не могут быть произвольными, а между ними должна существовать связь, которая носит название условий совместности или неразрывности деформаций. Зависимости существуют между компонентами деформаций в одной координатной плоскости и в разных плоскостях. Установим связь между составляющими деформации в одной плоскости. Для этого продифференцируем первое уравнение зависимости (1) дважды по 
, а второе – дважды по 
и полученные выражения сложим
Проведя подобные операции получим и для двух других плоскостей
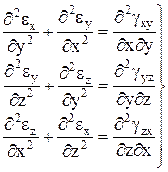(2)
Аналогичным образом можно выразить каждую линейную деформацию 
через сдвиговые 
.
Уравнение совместности показывает, что сплошное тело до деформации остается таковым и после нее. С энергетической точки зрения соблюдение условий совместности соответствует принципу минимума энергии деформации, т.к. любое нарушение сплошности деформируемой среды связано с дополнительной затратой энергии на образование разрывов.
Характеристики деформации
Для количественной оценки величины формоизменения, а также пластичности металлов существуют математические выражения, отражающие меру остаточной деформации.
Абсолютная деформация выражает абсолютное изменение какого-либо линейного или углового размера, площади сечения или поверхности выделенного участка либо всего тела
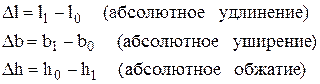
где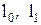 
- длина образца соответственно до и после деформации.
Относительная деформация – характеризует относительное изменение тех же величин
.
Она часто характеризует степень деформации тела, как общую величину его формоизменения. Условие постоянства объема 
.
|
|
Логарифмическая деформация, являющаяся разновидностью относительной деформации.
.
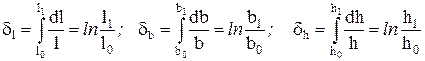Она обладает свойством аддитивности, т.е. сложения и может характеризовать суммарную деформацию тела. Поэтому ее часто называют истинной деформацией.
Пусть дано два этапа деформации
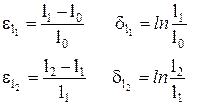
Полная величина деформации будет записана
, но 
.
Значит 
Между истинной и относительной деформациями существует связь
Из условия постоянства объема 
.
Отношение размеров тела после деформации к соответствующим начальным размерам называют коэффициентами деформации.
– коэффи-циент вытяжки.
– коэф-фициент уширения.
– коэф-фициент осадки.
Выражение 
- характеризует условие постоянства объема (несжимаемости).
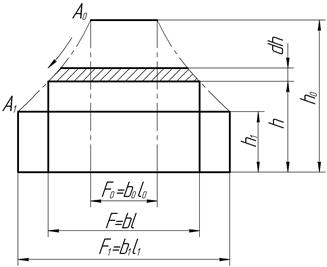
Смещенный объем
При определении работы, расходуемой на деформацию, пользуются понятием смещенного объема, представляющего прибавленный или удаленный в процессе деформирования объем в одном из главных направлений.
Смещенный по высоте объем при осадке на 
параллелепипеда, имеющего в данный момент высоту 
и площадь 
, равен
.
Учитывая, что 
, запишем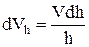 
.
За время осадки с высоты 
до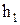 
и точка из положения 
смещается в 
.
Аналогично можно записать по двум другим направлениям
Из условия постоянства объема 
следует, что смещенный объем в одном из направлений равен сумме двух других с противоположным знаком.
Смещенный объем может быть меньше, равен и даже больше объема самого тела. Условие равенства этих объемов
|
|
или 
, т.е. 
Большие деформации
Технологические процессы ОМД характеризуются большими деформациями. Для их расчета следует пользоваться логарифмическими (истинными) деформациями, обладающими свойством аддитивности, коэффициентами деформации и смещенными объемами.