Лектор – доцент Чубаров И.А.

Экзаменационная программа курса «Линейная алгебра» для факультета

Биоинженерии и биоинформатики МГУ. 1 семестр 2011/2012 учебного года

Лектор – доцент Чубаров И.А.

1. Системы линейных уравнений. Алгоритм Гаусса упрощения системы линейных уравнений и матрицы. Главные и свободные неизвестные. Разложение общего решения неоднородной системы линейных уравнений в сумму частного решения и общего решения соответствующей однородной системы уравнений.

1. Матрицы. Сложение матриц, умножение матрицы на число, свойства этих операций.
2. Умножение матриц и его свойства. Обратная матрица, ее единственность. Транспонирование матриц. Транспонирование произведения. Обращение произведения.
3. Перестановки и подстановки, их знак. Понятие определителя квадратной матрицы: формула полного разложения. Свойства определителей (для транспонирования без доказательства). Определители диагональной и треугольной матриц.
4. Миноры, алгебраические дополнения, разложение определителя по строке и столбцу. Фальшивое разложение.
5. Лемма об определителе матрицы с углом нулей. Определитель произведения двух квадратных матриц. Исследование квадратной системы линейных уравнений. Формулы Крамера для решения квадратной системы линейных уравнений с ненулевым главным определителем.
6. Критерий существования и формула обратной матрицы. Вычисление обратной матрицы с помощью элементарных преобразований. Два способа решения матричных уравнений AX = B, XA = B (если ).
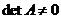7. Векторы на плоскости и в пространстве, линейные операции надними. Базис, координаты вектора в базисе, запись операций над векторами в координатах. Разложение вектора по базису на прямой, плоскости и в пространстве.
8. Скалярное произведение двух векторов. Выражение ортогональной проекции одного вектора на другой. Свойства скалярного произведение и его вычисление в координатах. Матрица Грама. Ортонормированный базис, разложение вектора по ортонормированному базису.
9. Векторное произведение двух векторов, его свойства (дистрибутивность без доказательства) и выражение в координатах. Критерий коллинеарности двух векторов.
10. Смешанное произведение трех векторов, его свойства, выражение в координатах. Объем ориентированного параллелепипеда. Критерий компланарности трех векторов.
11. Радиус-вектор точки. Декартова система координат. Выражение координат вектора через координаты его конца и начала. Прямоугольная (ортонормированная) декартова система координат. Формула расстояния между двумя точками.
12. Прямая на плоскости. Векторные уравнения прямой на плоскости: параметрическое и нормальное. Уравнения прямой на плоскости в координатах: каноническое, через две точки, общее линейное, с угловым коэффициентом. Взаимное расположение двух прямых на плоскости. Вычисление расстояния от точки до прямой, угла между двумя прямыми и расстояния между двумя параллельными прямыми на плоскости.
13. Прямая в пространстве. Векторное параметрическое уравнение прямой. Координатные формы уравнений прямой: параметрические, канонические, по двум точкам. Вычисление угла между двумя прямыми, расстояния от точки до прямой, расстояния между двумя параллельными и скрещивающимися прямыми в пространстве. Уравнения общего перпендикуляра двух скрещивающихся прямых*.
14. Плоскость в пространстве. Векторное параметрическое и нормальное уравнения плоскости, использование смешанного произведения. Координатные формы уравнения плоскости: общее, с помощью определителя, через 3 точки. Вычисление расстояния от точки до плоскости, угла между плоскостями, расстояния между параллельными плоскостями. Взаимное расположение двух плоскостей, прямой и плоскости в пространстве. Задание прямой как линии пересечения двух плоскостей (переход к параметрическим уравнениям).
15. Понятие базиса конечной совокупности матриц данных размеров (в частности, строк или столбцов). Определение ранга матрицы. Теорема о ранге матрицы. Вычисление ранга при помощи элементарных преобразований (алгоритм нахождения базисных столбцов).
16. Базисный минор, равенство ранга матрицы порядку ее базисного минора. Вычисление ранга методом окаймления миноров (формулировка метода). Критерий равенства определителя нулю.
17. Фундаментальная система решений однородной системы линейных уравнений. Общее решение однородной и неоднородной систем линейных уравнений. Теорема Кронекера-Капелли и ее следствие (условие единственности решения).
18. Определение линейного пространства. Примеры. Линейная зависимость и независимость векторов. Базис, постоянство числа векторов базиса данного пространства, размерность. Координаты вектора в базисе, запись операций над векторами в координатах. Матрица перехода от старого базиса к новому. Изменение координат вектора при изменении базиса.
19. Подпространства в линейном пространстве. Примеры. Линейная оболочка конечного набора векторов и ее размерность. Задание подпространства системой линейных однородных уравнений. Построение базиса (фундаментальной системы решений) в подпространстве решений однородной системы линейных уравнений.
20. Пересечение, сумма подпространств линейного пространства, связь их размерностей (без доказательства). Прямая сумма подпространств, условия, при которых сумма является прямой суммой.
21. Линейные отображения и преобразования (операторы) линейных пространств. Ядро и образ (множество значений) линейного отображения. Условие инъективности линейного отображения. Матрица линейного отображения; линейного оператора и ее изменение при замене базиса. Вычисление ядра и образа линейного отображения при помощи матрицы этого отображения.
22. Собственный вектор и собственноезначение линейного оператора и матрицы. Линейная независимость собственных векторов, отвечающих различным собственным значениям (доказательство для двух и трех векторов). Характеристическое уравнение и характеристический многочлен матрицы линейного оператора. Приведение матрицы линейного оператора к диагональному виду (необходимое и достаточное условие – существование базиса из собственных векторов; достаточное условие – наличие n различных собственных значений).
23. Евклидово пространство (пространство со скалярным произведением). Матрица Грама. Неравенство Коши-Буняковского. Ортонормированный базис, его построение по алгоритму ортогонализации (Грама-Шмидта) с последующим нормированием. Ортогональное дополнение; ортогональная проекция вектора на подпространство (только формулировки).

25. Билинейные и квадратичные функции, их матрицы. Положительно определенная квадратичная функция, ее канонический вид. Критерий Сильвестра положительной определенности (без доказательства).

26. *Изменение матрицы билинейной функции при замене базиса, неизменность ее ранга и знака определителя. Приведение квадратичной формы к каноническому (нормальному) виду методом выделения квадратов (алгоритм Лагранжа) (можно на примере).

Список литературы.

1. Умнов А.Е. Аналитическая геометрия и линейная алгебра. – М., 2006.

2. Кадомцев С.Б. Аналитическая геометрия и линейная алгебра. – М.: Физматлит, 2003.

3. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной алгебре.– М.: Физматлит, 2003.

4. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры.– М.: Наука, Физматлит, 2000.

5. Кострикин А.И. Введение в алгебру. Ч. I. Основы алгебры. Ч. II. Линейная алгебра. – М.: Физматлит, 2000 – 2005.

1. Шевцов Г.С. Линейная алгебра: теория и прикладные аспекты. М.: Финансы и

статистика, 2003.

7. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия. - М., МГУ, 1998.

Примечание. В билете один вопрос и одна задача. Формулировки идентичны формулировкам из программы. Некоторые пункты программы разбиты на два билета. Претендующие на 4 или 5 должны доказать хотя бы одну теорему из билета. Пункты или вопросы со * в билеты не включены, но могут использоваться как дополнительные вопросы.