Линейные модели не всегда являются адекватными реальным ситуациям. В действительности такие зависимости от плана производства, как общие затраты, себестоимость, выпуск продукции и т.п. носят нелинейный характер. Часто нелинейности в моделях обуславливаются непропорциональностью таких соотношений, как изменение затрат (эффект оптовости), выхода продукции, показателей качества.
Если для выпуска одного изделия необходимо 10 единиц сырья, то для выпуска 100 изделий надо 1000 ед. сырья.
Однако то, что справедливо для ресурсов, не всегда справедливо для экономических показателей.
Если себестоимость изготовления одного изделия равна 1 ед., то себестоимость 100 изделий составит не 100 ед., а значительно меньше.
Зависимость себестоимости от объема выпуска продукции является нелинейной, следовательно, и прибыль является нелинейной зависимостью.
Для решения задач, описываемых нелинейными моделями не существует универсальных методов (как симплекс-метод ЛП).
Какой-либо метод НЛП может оказаться эффективным для решения задач одного типа и совершенно неприемлемым для решения других задач.
Большинство методов НЛП не всегда обеспечивает сходимость за конечное число итераций. Некоторые методы обеспечивают монотонное улучшение значения целевой функции при переходе от одной итерации к другой.
Нелинейные задачи возникают в теории управления. Их исследование привело к возникновению в конце 40-х годов научной дисциплины НЛП.
Задача НЛП имеет следующий вид:
минимизировать или максимизировать целевую функцию:
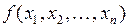
при ограничениях
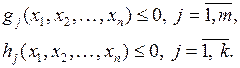
В векторных обозначениях соотношения записываются в более компактном виде:
минимизировать f (x)
|
|
при ограничениях g (x)£0, h (x)=0,
где f, g, h – функции, отображающие каждую точку n -мерного пространства.
К нелинейному программированию относятся те задачи, в которых целевая функция нелинейная или имеется, по крайней мере, одно нелинейное ограничение на переменную x.
Общая задача НЛП формулируется следующим образом:
Требуется найти n -мерный вектор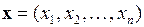 
, который минимизирует (максимизирует) целевую функцию и удовлетворяет заданным ограничениям.
Геометрически, функция цели задачи НЛП описывает местность с оврагами и возвышенностям, а ограничения описывают часть территории на этой местности. Необходимо найти самую низкую (высокую) точку местности на ограниченной территории.
Наименьшее или наибольшее значение линии уровня функции цели на этой территории является оптимальным, а общие точки линии уровня и области допустимых решений являются решением задач НЛП.
Решение задачи может быть внутри области допустимых решений или на ее границе.
Функция цели обычно имеет несколько локальных экстремумов, что затрудняет поиск глобального минимума (максимума).
Пример:
Требуется спроектировать ангар вформе параллелепипеда с открытой передней стенкой и без дна. Конструкция должна иметь объём 16000 м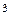 
, но периметр р её основания не должен превышать 220 м. Длина l не должна быть больше 60 м, ширина s – не больше 70 м. Кроме того, ширина не должна превышать утроенной длины (
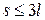), а высота – 2/3 ширины (
).
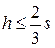Стоимость материала, из которого изготавливается конструкция составляет 30 руб./м 
. Требуется определить такие размеры конструкции, чтобы минимизировать стоимость материалов.
|
|
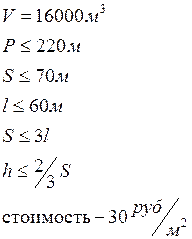
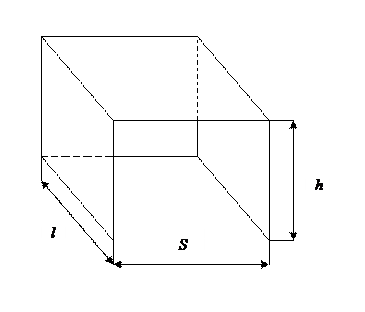
Введём переменные:
.
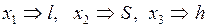Стоимость материалов будет включать:
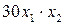– стоимость крышки,
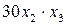– стоимость задней стенки,
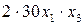– стоимость боковой стенки.
Следовательно целевая функция имеет вид:
.
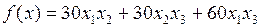Условие объема задает ограничение в виде равенства
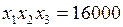м3.
Условия на линейные размеры задают ограничения в виде неравенств:
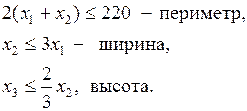
Границами изменения переменных являются:
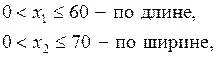
x 3³0
Т.к. в ц.ф. и ограничениях произведение переменных – это задача НЛП.
В стандартной форме записи задача имеет вид:
,
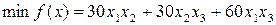при ограничениях:
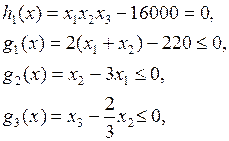
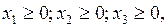
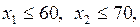
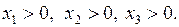
Результата решения задачи:
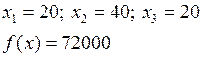
Т.о. получен минимальный расход материалов.