Пусть точки  являются концами линии
являются концами линии 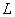 , а сама она задана функцией одной переменной
, а сама она задана функцией одной переменной  . Тогда криволинейный интеграл первого рода можно свести к обычному определённому интегралу по следующей формуле:
. Тогда криволинейный интеграл первого рода можно свести к обычному определённому интегралу по следующей формуле:

Знак модуля обусловлен природой рассматриваемого интеграла: поскольку дифференциал  не может быть отрицательным (это же элемент длины), то при переходе к определённому интегралу нужно соблюсти статус-кво. В случае «арабского» интегрирования справа налево (когда
не может быть отрицательным (это же элемент длины), то при переходе к определённому интегралу нужно соблюсти статус-кво. В случае «арабского» интегрирования справа налево (когда  ) значения «икс» убывают и поэтому
) значения «икс» убывают и поэтому  – в результате чего появляется побочный минус, подлежащий немедленной ликвидации. Общую формулу можно расписать подробно:
– в результате чего появляется побочный минус, подлежащий немедленной ликвидации. Общую формулу можно расписать подробно:
 , если
, если  (стандартный случай) или:
(стандартный случай) или:
 , если
, если  .
.
В частности, при  получается хорошо знакомая формула длины дуги кривой
получается хорошо знакомая формула длины дуги кривой  . Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже решали! И теперь вам совсем не нужно решимости:)
. Вот так-то оно бывает – оказывается, криволинейные интегралы мы уже решали! И теперь вам совсем не нужно решимости:)
Пример 1
Вычислить интеграл 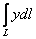 от точки
от точки  до точки
до точки  , если кривая
, если кривая 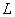 задана уравнением
задана уравнением 
Решение: перед нами каноническое уравнение параболы, и коль скоро в условии дана точка  , то речь идёт о её верхней ветке:
, то речь идёт о её верхней ветке: 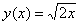 .
.
Желающие могут выполнить чертёж. Кстати, вне зависимости от его простоты, иногда это бывает обязательным требованием условия.
В данной задаче имеет место наиболее распространённый случай  , а значит, нужно использовать формулу
, а значит, нужно использовать формулу  .
.
Сначала удобно найти производную и упростить корень:

Так как  и
и 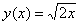 , то
, то  – грубо говоря, на данном шаге мы избавляемся от «игреков».
– грубо говоря, на данном шаге мы избавляемся от «игреков».
Предварительная подготовка завершена, пользуемся формулой:

Здесь можно провести замену переменной, но гораздо сподручнее подвести подкоренное выражение под знак дифференциала и обойтись без перехода к новым пределам интегрирования:

Ответ: 
Если вычислить тот же самый интеграл от точки  до точки
до точки  , то результат не изменится. В этом случае «икс» будет убывать от 1 до 0, следовательно, дифференциал
, то результат не изменится. В этом случае «икс» будет убывать от 1 до 0, следовательно, дифференциал  станет отрицательным и при переходе к определённому интегралу потребуется добавить знак «минус»:
станет отрицательным и при переходе к определённому интегралу потребуется добавить знак «минус»:
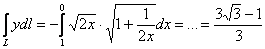
Таким образом, криволинейный интеграл 1-го рода не зависит от направления интегрирования: 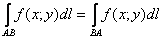
В этой связи типовая задача, как правило, формулируется «нейтрально»: вычислить интеграл 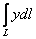 вдоль дуги параболы
вдоль дуги параболы  , расположенной между точками
, расположенной между точками  . Иными словами, совершенно не важно, какая из точек является началом, а какая – концом кривой.
. Иными словами, совершенно не важно, какая из точек является началом, а какая – концом кривой.
Следует отметить, что криволинейный интеграл можно вычислить и другим способом. Поскольку буква «игрек» ничем не хуже «икса», то для вычисления криволинейного интеграла 1-го рода справедлива «зеркальная» формула (тривиальный вариант  ):
):
 , где
, где  – обратная функция, выражающая линию
– обратная функция, выражающая линию 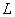 . В нашей задаче:
. В нашей задаче:

При переходе от 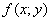 к
к  мы должны избавиться от всех «иксов», однако функция
мы должны избавиться от всех «иксов», однако функция  от них не зависит, а значит, делать ничего не нужно.
от них не зависит, а значит, делать ничего не нужно.
И, учитывая, что для «игрековых» координат точек  справедливо неравенство
справедливо неравенство  , доводим решение до того же самого результата:
, доводим решение до того же самого результата:

В чём состоит геометрический смысл разобранной задачи? На плоскости  между точками
между точками 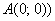 и
и  находится кусок параболы
находится кусок параболы  , через который проходит «одноимённый» параболический цилиндр
, через который проходит «одноимённый» параболический цилиндр  , «высекающий» из плоскости
, «высекающий» из плоскости  пространственную «ниточку». Криволинейный интеграл
пространственную «ниточку». Криволинейный интеграл 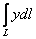 численно равен площади
численно равен площади  фрагмента параболического цилиндра, который расположен между куском параболы и этой «ниткой».
фрагмента параболического цилиндра, который расположен между куском параболы и этой «ниткой».
Как я уже отмечал, криволинейный интеграл может получиться отрицательным – это означает, что фрагмент полностью или бОльшей частью лежит ниже плоскости  . Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов».
. Не удивляйтесь и нулю (в каких случаях?). То есть, «всё как у нормальных интегралов».
Замысловатый пример для самостоятельного решения:
Пример 2
Вычислить площадь фрагмента цилиндрической поверхности  во 2-м и 6-м октантах
во 2-м и 6-м октантах  , который высечен плоскостью
, который высечен плоскостью  и гиперболическим параболоидом
и гиперболическим параболоидом  .
.
Ситуацию крайне важно представить геометрически – надеюсь, на данный момент все знают, как выглядит круговой цилиндр  ; картинку же последней поверхности можно найти в начале урока об экстремумах функций двух и трёх переменных (3-й чертёж). Также будет полезно изобразить на плоскости
; картинку же последней поверхности можно найти в начале урока об экстремумах функций двух и трёх переменных (3-й чертёж). Также будет полезно изобразить на плоскости  кривую интегрирования.
кривую интегрирования.
Краткое решение с комментариями в конце урока – тот, кто правильно во всём разберётся, может считать себя «самоваром» интегралов =)
Довольно часто линия 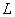 бывает задана параметрическими уравнениями
бывает задана параметрическими уравнениями  , и в этом случае нужно использовать следующую формулу:
, и в этом случае нужно использовать следующую формулу:
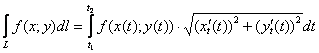 – если значение параметра возрастает
– если значение параметра возрастает  . И для убывающего параметра
. И для убывающего параметра 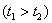 :
:

В частности, при  получается опять же знакомая формула длины параметрически заданной кривой:
получается опять же знакомая формула длины параметрически заданной кривой:

Пример 3
Вычислить криволинейный интеграл 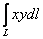 по дуге окружности
по дуге окружности  при изменении параметра
при изменении параметра  .
.
Параметрические уравнения эллипса и окружности я разбирал в тематической статье о площади и объёме, и поэтому если вам не понятен их смысл (или вообще смысл параметрического задания функции), то милости прошу по ссылке.
Решение: указанным пределам изменения параметра соответствует левая верхняя дуга единичной окружности:

По условию, значение параметра возрастает, поэтому:
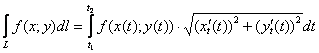
Нет, конечно, можно интегрировать и от  до
до  с добавочным минусом, но зачем?
с добавочным минусом, но зачем?
Как и в предыдущих примерах, сначала удобно найти производные и причесать корень:

…мда, тут вообще стрижка наголо получилась =)
Итак:

Ответ: 
Два последних примера похожи, как близкие родственники, однако между ними есть существенное различие: в Примере 2 требовалось найти площадь, и поэтому было принципиально важно проанализировать положение поверхности  относительно плоскости
относительно плоскости  . В третьем же примере нужно было вычислить интеграл формально. Как видите, различие здесь точно такое же, как и между вычислением площади с помощью определённого интеграла и «просто» вычислением определённого интеграла.
. В третьем же примере нужно было вычислить интеграл формально. Как видите, различие здесь точно такое же, как и между вычислением площади с помощью определённого интеграла и «просто» вычислением определённого интеграла.
И, разумеется, криволинейные интегралы обладают всеми типичными свойствами «клана интегралов», в частности, для них справедливо свойство линейности:

а также свойство аддитивности: если на линии  выбрать промежуточную точку
выбрать промежуточную точку  , то интеграл можно разделить на две части:
, то интеграл можно разделить на две части:

Или вот такой – более практически важный пример, …сейчас что-нибудь придумаю, чтобы легко было нарисовать в уме,… предположим, нам нужно вычислить криволинейный интеграл по ломаной 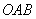 :
:
 , где
, где  .
.
Да без проблем – представим его в виде суммы двух интегралов по отрезкам  :
:
 – и вперёд с песнями.
– и вперёд с песнями.
И на всякий пожарный формула для кривой, заданной уравнением  в полярных координатах:
в полярных координатах:

Кроме того, у криволинейного интеграла 1-го рода существуют физические приложения, в частности, с помощью него можно вычислить массу плоской дуги  , если
, если 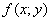 – функция её плотности.
– функция её плотности.