Лекции 1-2. Матрицы, действия с ними. Определители 2-3 порядков. Их свойства. Разложение определителей по элементам строк и столбцов. Определители n-ого порядка. Системы двух и трех линейных уравнений. Правило Крамера. Обобщение результатов на системы n-линейных уравнений. Линейные однородные системы и их нетривиальные решения.
ЛИТЕРАТУРА:
Бугров Я.С., Никольский С.М.Высшая математика, Т.1,. Элементы линейной алгебры и аналитической геометрии. М., Дрофа, 2003. && 1- 4. Л-3, гл.21.
Ефимов Н.В. Краткий курс аналитической геометрии. М.Физматлит, 2002.. Приложение.
И.П. Натансон. Краткий курс высшей математики.,М.,Лань.2005,гл.7.
На этой лекции мы с вами начнем изучение математических объектов, называемых матрицами. Начнем с определения матрицы.
Определение. Матрицей A называется прямоугольная таблица чисел, которую будем представлять в виде.
A=  .
.
Элементы, стоящие на одной горизонтали будем называть строками, на одной вертикали столбцами. Если матрица содержит  строк и
строк и  столбцов, то будем говорить, что матрица имеет размерность
столбцов, то будем говорить, что матрица имеет размерность 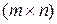 . Символом
. Символом  обозначается элемент, стоящий на пересечении строки с номером i и столбца с номером j. В случае, когда число строк равно числу столбцов (
обозначается элемент, стоящий на пересечении строки с номером i и столбца с номером j. В случае, когда число строк равно числу столбцов ( ), матрица называется квадратной.
), матрица называется квадратной.
Например. Пусть имеется матрица
 .
.
Определим размерность данной матрицы. Надеюсь, что это не очень сложно посчитать – данная матрица имеет 4 строки и 5 столбцов. Тогда ее размерность соответственно равна  . Зададимся вопросом – чему равен, например
. Зададимся вопросом – чему равен, например  . Нетрудно видеть, что на пересечении второй строки и третьего столбца стоит число 4. Следовательно,
. Нетрудно видеть, что на пересечении второй строки и третьего столбца стоит число 4. Следовательно,  =4.
=4.
Иногда, когда позволяют обстоятельства, мы будем использовать краткую запись  , которая подразумевает, что имеется матрица, с элементами
, которая подразумевает, что имеется матрица, с элементами  , размерность которой нам известна.
, размерность которой нам известна.
Введение в математике некоторых объектов, как правило, влечет за собой введение некоторых математических операций над ними. Но любые математические операции подразумевают, в итоге, знак равенства. Поэтому прежде нужно договориться о том, какие матрицы мы считаем равными.
Определение. Матрица  равна матрице
равна матрице 
 тогда и только тогда, когда они имеют одинаковую размерность и на одинаковых местах у них стоят равные элементы, то есть
тогда и только тогда, когда они имеют одинаковую размерность и на одинаковых местах у них стоят равные элементы, то есть  .
.
Например. Ответим на вопрос, какие пары матриц можно считать равными
1. 
2.  .
.
3.  .
.
В первой паре матрицы имеют разную размерность, поэтому они не равны друг другу.
Во второй паре матрицы имеют одинаковую размерность, но элемент  , а элемент
, а элемент 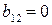 , то есть, не равны друг другу. Следовательно, и эти две матрицы не являются равными.
, то есть, не равны друг другу. Следовательно, и эти две матрицы не являются равными.
В третьей паре матрицы являются равными.
Теперь перейдем к математическим операциям.
Сложение матриц.
Операция сложения определена только для матриц одинаковой размерности.
Определение. Пусть даны матрицы  и
и  размерности
размерности 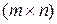 . Их сумма
. Их сумма  , где матрица
, где матрица  имеет размерность также
имеет размерность также 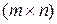 , а элементы ее
, а элементы ее  соответственно равны
соответственно равны  .
.
(То есть, элементы, стоящие на одинаковых местах просто складываются.)
Нетрудно видеть, что операция сложения матриц обладает свойствами: коммутативности  ;
;
ассоциативности  .
.
Пример. Найти  , если
, если 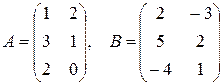 .
.
Имеем 
Следующая операция, это операция умножения матрицы на действительное число.
Умножение матрицы на действительное число.
Определение. Пусть даны матрица  размерности
размерности 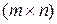 . Произведением матрицы
. Произведением матрицы  на число
на число  (
( ) называется матрица
) называется матрица  ,, где матрица
,, где матрица  имеет размерность также
имеет размерность также 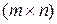 , а элементы ее
, а элементы ее  соответственно равны
соответственно равны  .
.
(То есть, все элементы матрицы  умножаются на число
умножаются на число  ).
).
Пример. Найти  , если
, если  .
.
Имеем  .
.
Не трудно проверить следующие свойства операции умножения на число:
1.  ;
;
2.  .
.
Следующая операция, это произведение матриц.
Произведение матриц.
Произведение матриц АВ=С определено только тогда, когда число столбцов в первом множителе (матрица А) равно числу столбцов во втором множителе (матрица В). Результат произведения (матрица С) имеет столько строк, сколько у первого множителя (матрицы А), число столбцов матрицы С равно числу столбцов у второго множителя (матрицы В). Ниже будет указан способ вычисления элементов матрицы С.
Пусть  размерности
размерности  ,
,  - размерности
- размерности  . Тогда
. Тогда  (С=АВ) имеет размерность
(С=АВ) имеет размерность  . Элементы матрицы
. Элементы матрицы  вычисляются по формуле
вычисляются по формуле  =
=  .
.
(То есть элементы строки с номером i в первой матрицы умножаются на соответствующие элементы столбца с номером j во второй матрице и полученные произведения складываются.)
Рассмотрим пример.
Найти матрицу С=АВ, если  ,
,  .
.
Поскольку первый множитель имеет две строки, а второй два столбца, то матрица  имеет размерность
имеет размерность 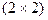 .
.  . Определим элементы матрицы С.
. Определим элементы матрицы С.
При вычислении  берем первую строку матрицы А - (2 0 1) и первый столбец матрицы В -
берем первую строку матрицы А - (2 0 1) и первый столбец матрицы В -  , почленно перемножаем и складываем
, почленно перемножаем и складываем  =2
=2  3+0
3+0  1+1
1+1  5=11.
5=11.
Аналогично находим:
n  . Первая строка А - (2 0 1), второй столбец В -
. Первая строка А - (2 0 1), второй столбец В -  , тогда
, тогда  =2
=2  4+0
4+0  0+1
0+1  2=10;
2=10;
n  . Вторая строка А - (3 2 4), первый столбец В -
. Вторая строка А - (3 2 4), первый столбец В -  , тогда
, тогда 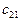 =3
=3  3+2
3+2  1+4
1+4  5=31;
5=31;
n  . Вторая строка А - (3 2 4), второй столбец В-
. Вторая строка А - (3 2 4), второй столбец В-  , тогда
, тогда  =3
=3  4+2
4+2  0+4
0+4  2=20.
2=20.
Ответ:  .
.
Нетрудно показать, что операция произведения матриц удовлетворяет следующим свойствам:
1.  .
.
2. 
Отметим, что в общем случае АВ¹ВА.
Например. Дома вычислите самостоятельно  и
и  , если
, если

Введем понятие единичной матрицы. Единичной матрицей называется квадратная матрица Е размерности  , у которой все элементы на главной диагонали равны 1, а остальные нулю. Например, единичная матрица размерности (3
, у которой все элементы на главной диагонали равны 1, а остальные нулю. Например, единичная матрица размерности (3  3) имеет вид
3) имеет вид  . Элементы единичной матрицы часто обозначают символом
. Элементы единичной матрицы часто обозначают символом  , где
, где  - символ Кронекера
- символ Кронекера  .
.
Отметим, что для любой матрицы А той же размерности имеет место равенство АЕ=ЕА=А.
Введем еще одну операцию – транспонирование матрицы.
Транспонированная матрица.
Определение. Пусть дана матрица  размерности
размерности 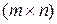
.
Матрицу  называют транспонированной к матрице
называют транспонированной к матрице  , если она имеет размерность
, если она имеет размерность  , и при этом
, и при этом  . То есть, матрица
. То есть, матрица  получается из матрицы
получается из матрицы  следующим образом – столбцы матрицы
следующим образом – столбцы матрицы  становятся строками матрицы
становятся строками матрицы  , причем номер соответствующего столбца матрицы
, причем номер соответствующего столбца матрицы  совпадает с номером соответствующей строки матрицы
совпадает с номером соответствующей строки матрицы  . Транспонированную к матрице
. Транспонированную к матрице  матрицу будем обозначать символом
матрицу будем обозначать символом  или
или 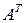 .
.
Тогда, если

 ,
,
то

 ,
,
Пример. Найти  , если
, если  .
.
Получаем  =
=  .
.
Пример. Найти  , если
, если  .
.
Получаем  =
=  .
.
Далее мы введем еще одно понятие – определитель матрицы.
Понятие определителя имеет смысл только для квадратной матрицы. Определитель - это некоторое число, которое ставится в соответствие квадратной матрице  . Оно обозначается символом D или
. Оно обозначается символом D или  . Иногда вместо слова определитель употребляется термин детерминант, и определитель матрицы
. Иногда вместо слова определитель употребляется термин детерминант, и определитель матрицы  обозначается
обозначается  . Ниже будет изложено правило его вычисления. Мы используем рекурсивный способ задания метода вычисления определителя. Суть его в следующем. Сначала мы укажем способ вычисления определителя матрицы размерности (
. Ниже будет изложено правило его вычисления. Мы используем рекурсивный способ задания метода вычисления определителя. Суть его в следующем. Сначала мы укажем способ вычисления определителя матрицы размерности ( ), а далее будет указан метод, который позволяет вычислять определитель матрицы размерности
), а далее будет указан метод, который позволяет вычислять определитель матрицы размерности  , если мы умеем вычислять определитель матрицы размерности
, если мы умеем вычислять определитель матрицы размерности  .
.
И так начнем.
Для матрицы А размерности  А=
А=  по определению
по определению
 .
.
Далее введем еще одно определение.
Минором  матрицы А называется определитель матрицы, получаемой из матрицы А путем удаления строки с номером i и столбца с номером j.
матрицы А называется определитель матрицы, получаемой из матрицы А путем удаления строки с номером i и столбца с номером j.
Например, для матрицы 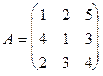 имеем
имеем  .
.
Алгебраическим дополнением элемента 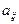 называется число, равное значению минора
называется число, равное значению минора  , если i+j четное, и равное значению минора с противоположным знаком (-
, если i+j четное, и равное значению минора с противоположным знаком (-  ) в противном случае. Алгебраическое дополнение будем обозначать символом
) в противном случае. Алгебраическое дополнение будем обозначать символом  . Таким образом
. Таким образом  .
.
Например, для матрицы  имеем
имеем  .
.