Тогда, для матрицы второго порядка имеем 
. С ее помощью вычислим определитель
Запомним полученную формулу вычисления определителя матрицы второго порядка. С ее помощью вычислим определитель 
.
Теперь перейдем к матрице третьего порядка.
Для матрицы третьего порядка
=
.
.
Запоминать полученное соотношение рекомендуется. Лучше запомнить сам прием и его суть. Вычисление определителя третьего порядка свелось к вычислению трех определителей второго порядка. Точно по такой же схеме вычисление определителя матрицы порядка 
сводится к вычислению определителя матриц порядка 
.
Вычислим определитель третьего порядка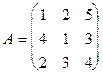 
. Имеем
.
Аналогично, для матрицы четвертого порядка имеем
=
.
Далее мы изучим свойства определителей. Мы будем их изучать на примере определителей третьего порядка, однако они имеют место для определителей любого порядка.
Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы 
.
На примере матрицы третьего порядка имеем.
Пусть 
, следовательно
.
Тогда 
=
= .
Как видим, действительно 
.
Принципиальный вывод, который следует из данного свойства, состоит в том, что строки и столбцы в определителе равноправны. Операция транспонирования превращает любой столбец в строку и наоборот. Поэтому последующие свойства мы будем формулировать сразу и для строк и для столбцов.
Свойство 2. При перестановке двух строк (или столбцов) местами знак определителя меняется на противоположный.
Предлагается проверить сам0стоятельно.
Например 
.
Свойство 3. Если матрица 
имеет две равные строки (или два равных столбца), то ее определитель равен нулю.
Доказательство. Пусть матрица имеет две равные строки и ее определитель равен 
. Матрицу, полученную из матрицы перестановкой этих самых двух равных строк, обозначим 
.
Поскольку строки переставлены, то, в силу свойства 2, для определителя матрицы имеем 
. Но поскольку переставлялись равные строки, то 
. Значит, 
. Получаем 
, и, следовательно 
.
Свойство 4. Если все элементы некоторой строки (или столбца) умножить на постоянный множитель 
, то определитель умножается на этот же множитель 
.
Например.
.
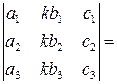
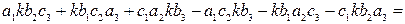
Свойство 5. Если все элементы некоторой строки (или столбца) матрицы равны нулю, то ее определитель равен нулю.
Доказательство следует из свойства 4, полагая 
.
Свойство 6. Если две строки (или два столбца) матрицы пропорциональны, то ее определитель равен нулю.
Доказательство. Пусть пропорциональны первый и второй столбцы. Имеем 
(в силу свойства 4)= 
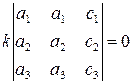, поскольку в матрице имеются два равных столбца.
Следующее свойство проще записать в виде соотношения. Формулировка займет слишком много места. Суть его состоит в том, что если некоторая строка (или столбец) представлены в виде суммы каких-то двух строк (или столбцов), то определитель такой матрицы можно представить в виде суммы определителей матриц определенного вида.
Свойство 7. 
.
Доказать самостоятельно.
Свойство 8. Определитель матрицы не изменится, если к элементам одной строки (или столбца) прибавить соответствующие элементы другой строки (или столбца) умноженные на постоянный множитель.
Доказательство. В силу свойства 7
Но поскольку во втором определителе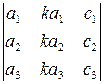 
первый и второй столбцы пропорциональны, то в силу свойства 6 он равен нулю. Следовательно,
.
Свойство 9. Определитель равен сумме произведений элементов любой строки (или столбца) на их алгебраические дополнения.
Как показано ранее
.
Рассмотрим для примера сумму произведений элементов третьего столбца на их алгебраические дополнения. Получаем
=
= 
= 
.
Аналогичным образом можно провести проверку и для других строк и столбцов. Представление определителя в виде сумме произведений элементов некоторой строки или столбца на их алгебраические дополнения называется разложением по элементам этой строки или столбца.
Рассмотрим матрицу 
. Алгебраические дополнения соответствующих элементов будем обозначать теми же символами, только большими 
.
В силу свойства 9 имеем 
(сумма произведений элементов первого столбца на их алгебраические дополнения).
Рассмотрим сумму вида 
. Нетрудно видеть, что эта сумма является определителем следующей матрицы
.
Пусть 
.
Тогда 
.
Теперь можно сформулировать еще одно свойство.
Свойство 10. Сумма произведений элементов некоторой строки (или столбца) на алгебраические дополнения к соответствующим элементам другой строки (или другого столбца) равна нулю.
В заключение отметим без доказательства тот факт, что определитель произведения матриц равен произведению их определителей, то есть
.
В ранее рассмотренном примере вычисления определителя четвертого порядка были специально подробно проведены все промежуточные выкладки, чтобы отметить один из существенных недостатков предложенного алгоритма. Оценим необходимое количество операций для его выполнения. Определитель матрицы порядка 
сводится к вычислению определителей матриц порядка 
. Каждый из определителей матриц порядка сводится к вычислению определителя матриц порядка 
. Таким образом вычисление определителя по подобной схеме требует количества операций порядка 
. При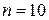 
имеем 
. То есть с ростом размерности матрицы количество операций очень быстро возрастает. Отметим также, что предложенный алгоритм обладает и другими недостатками, связанными с ограниченностью разрядной сетки представления чисел, что может привести к значительной потере точности вычисления определителя для матриц большой размерности при вычислении на ЭВМ.
Можно привести другой метод вычисления определителя, основанной на той же схеме, но который свободен от некоторых указанных недостатков.
Для этого напомним еще два свойства определителя.
1. При перестановке двух строк (или столбцов) определитель меняет знак на противоположный.
2. Определитель не изменится, если к элементам одной строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на некоторый множитель.
Отметим, что если все элементы некоторого (например первого) столбца кроме одного (например самого первого) равны нулю, то вычисление определителя матрицы порядка сводится к вычислению одного определителя матрицы порядка . Первое свойство позволяет на начальном этапе изменить матрицу так, что первый элемент первого столбца будет не равным нулю. Вычислим теперь тот же определитель с применением этих свойств.
.
Из второй строки вычтем первую, умноженную на 2; из третьей вычтем первую, умноженную на 3; из четвертой вычтем первую.
Тогда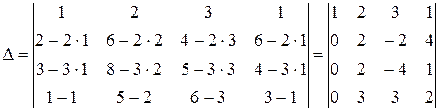 
.
Разложив определитель по первому столбцу, получаем 
.
Проведем аналогичные действия с полученным определителем Из второй строки вычтем первую; из третьей строки вычтем первую, умноженную на множитель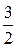 
.
.
Разложим по первому столбцу 
.
Оценим количество операций, которое требует данный метод.
Для того, чтобы обнулить первый элемент в некоторой строке путем прибавления первой строки, умноженной на соответствующий множитель для матрицы порядка требуется операций. Всего имеется строк. Следовательно, для того, чтобы свести вычисление определителя матрицы порядка к вычислению одного определителя матрицы порядка 
число требуемых операций имеет порядок 
. Следовательно, число операций, которое требуется для вычисления определителя, имеет порядок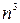 
. Для больших значений величина 
существенно меньше 
.
Закачивая изучение определителей, рассмотрим пример.
1. Решить уравнение
.
Решение. Раскладывая по третьему столбцу, получаем
.
Вычислим каждый из определителей, входящих в это уравнение. (Вычисление последнего не требуется.)
;
;
.
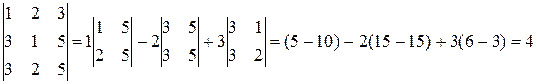Подставляя в уравнение, получаем
Теперь мы перейдем к новой теме, в которой мы используем аппарат теории определителей. Ведь определители возникли не как игра ума математиков. Просто теория определителей потребовалась для решения некоторых задач.
Мы рассмотрим применение теории определителей для исследования систем линейных уравнений. Система линейных уравнений с неизвестными имеет вид
Мы продолжим изучение на примере систем трех линейных уравнений с тремя неизвестными, однако полученные результаты будут верны и для любых систем, когда число уравнений совпадает с числом неизвестных.
Системой трех линейных уравнений с тремя неизвестными (x,y,z) называется система уравнений вида:
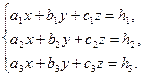
Решением системы называется любой набор неизвестных (x,y,z), при подстановке которых в уравнения системы все уравнения превращаются в числовые равенства.
Решить систему – это найти множество всех ее решений, или доказать, что решений нет.
Система уравнений, которая имеет решение называется совместной, если система уравнений не имеет решений, то она называется несовместной.
Матрицей системы называется матрица А, составленная из коэффициентов при неизвестных: 
.
Определителем системы D называется определитель матрицы А 
.
Алгебраические дополнения соответствующих элементов будем обозначать теми же символами, только большими 
.
Столбцом свободных 
называется столбец вида: 
.
Предположим, что система имеет решение. Тогда первое уравнение системы умножим на 
, второе на 
, третье на 
, и сложим.
Получаем
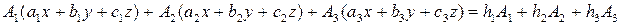
Преобразуем полученное уравнение к виду
.
Заметим, что выражение 
представляет собой сумму произведений элементов первого столбца матрицы А на их алгебраические дополнения. Согласно свойству 9 определителей, она равна определителю матрицы А, то есть определителю системы - 
.
Суммы вида 
представляют собой сумму произведений элементов второго и третьего столбцов матрицы А на алгебраические дополнения к соответствующим элементам первого столбца. Согласно свойству 10 определителей, они равны нулю 
.
Последняя сумма 
представляет собой определитель вида
, то есть определитель матрицы, получаемой из матрицы системы путем замены столбца коэффициентов при неизвестном 
столбцом свободных членов. Обозначим
.
Таким образом, получаем 
.
Аналогично, умножая первое уравнение системы на 
, второе на 
, третье на 
, и складывая, получаем 
, где 
- определитель матрицы, получаемой из матрицы системы путем замены столбца коэффициентов при неизвестном 
столбцом свободных членов
.
Умножая первое уравнение системы на 
, второе на 
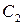, третье на 
, и складывая, получаем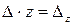 
, где 
- определитель матрицы, получаемой из матрицы системы путем замены столбца коэффициентов при неизвестном 
столбцом свободных членов
.
Таким образом, мы получили систему уравнений вида
.
Полученная система позволяет сделать два важных вывода.
Вывод первый. Если определитель системы равен нулю 
, а хотя бы один из определителей 
, , не равен нулю, то система не имеет решения.
Вывод второй. Если определитель системы не равен нулю 
и система имеет решение, то решение имеет вид
, 
, 
.
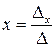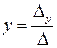Покажем, что в случае, когда определитель системы не равен нулю , соотношения 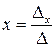, , 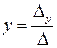действительно определяют решение системы.
Для этого подставим полученные значения неизвестных в уравнения системы, например в первое
Получаем
Заметим, что
; 
; 
.
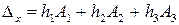Тогда получаем
=
= 
.
Успех проводимых математических преобразований во многом определяется формой записи выражений. Перепишем полученное соотношение в несколько иной форме, перегруппировав слагаемые
=
= 
.
Заметим, что сумма вида 
представляет собой сумму произведений элементов первой строки матрицы системы на их алгебраические дополнения, и, следовательно, равна определителю системы
.
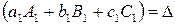Суммы вида 
, 
представляет собой сумму произведений элементов первой строки матрицы системы на алгебраические дополнения к элементам второй и третьей строки, и, следовательно, равны нулю =0, 
=0.
Тогда получаем
== 
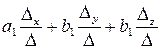Нам остается только порадоваться, поскольку именно это мы и пытались доказать.
Вывод. Если определитель системы не равен нулю , то система имеет единственное решение при этом неизвестные (x,y,z) определяются формулами,
, , ,
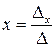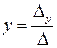которые называются формулами Крамера.
Рассмотрим примеры.
Решить систему уравнений 
.
Имеем
;
;
.
Тогда 
.
Пример. Решить систему 
Определитель системы равен 
= 
.
Определители 
, 
, 
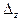соответственно равны:
,
,
.
Получаем: x= 
, y= 
, z= 
.
В заключении данной темы рассмотрим еще одно понятие.
Система линейных уравнений называется однородной, если столбец свободных членов равен нулю. То есть однородная система в случае трех уравнений с тремя неизвестными имеет вид
Однородная система линейных уравнений всегда имеет нулевое решение 
, 
, 
,
Если определитель системы не равен нулю, то это решение является единственным. Следовательно, однородная система линейных уравнений всегда имеет ненулевое решение только в том случае, когда ее определитель равен нулю. Этот факт довольно часто встречается на практике. Простейший пример. Если вы возьмете линейку, поставите ее вертикально, и надавите сверху рукой, то в какой-то момент она начнет выпучиваться. Тот факт, что при некотором усилии у линейки, помимо сжатого, появляется и изогнутое состояние равновесия, связан с тем, что некоторая однородная система линейных уравнений имеет ненулевое решение. То есть определитель соответствующей матрицы обращается в ноль. Это условие и позволяет определить соответствующую критическую нагрузку.
В заключении рассмотрим пример.
Пример. Доказать, что если система уравнений
имеет решение, то определитель
Решение. Предположим, что система имеет решение 
. Рассмотрим однородную систему четырех уравнений с четырьмя неизвестными
Эта система тогда имеет решение 
, то есть ненулевое. А это означает, что ее определитель равен нулю. Следовательно,
.
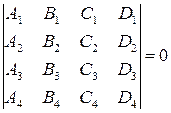