В геометрических задачах № 13, № 16 (базовый уровень) и № 8 (профильный уровень) каждый второй ученик делает ошибки. Здесь тоже существует довольно полезный механизм поиска решения, который состоит из 3 вопросов, которые должен задать себе обучающийся (порядок вопросов менять нельзя).
1) Может быть это подобие (в задаче есть 2 фигуры, внешне погожи одна на другую, но разные по размеру), если да, то записать k – это изменение любого линейного размера, k2 – если речь идет о площади, k3 – если речь идет об объеме.
2) Может быть отрезана часть, если да, то нужно обязательно понять какая.
Примеры:
1) в треугольнике проведена средняя линия, она отсекает 1/4 часть;
2) через середины соседних сторон квадрата проведен отрезок, он отсекает 1/8 часть от всего квадрата;
3) в правильном шестиугольнике АВСДЕК проведена диагональ АС, она отсекает треугольник, равный 1/6 всего шестиугольника и такие части можно увидеть и при решении многих других задач.
Ученик просто должен знать, что если он ответил на этот вопрос утвердительно, то следующим этапом является, понимание какую часть он будет рассматривать.
3) Если на первые два вопроса получен отрицательный ответ, то это формула и возможно теорема Пифагора. В тексте звучит название формулы (объем, площадь поверхности и т.д.). В этом случае записать формулу и все правильно подставить. Здесь часто встречается теорема Пифагора. Наличие корней в тексте задачи почти прямое указание на эту теорему.
Теперь более подробно разберем эту схему при решении задач.
1) В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.
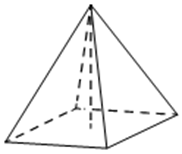
Решение: Это не подобие, это не части, значит здесь применяется формула объема пирамиды и теорема Пифагора. Боковое ребро, высота и половина диагонали основания составляют прямоугольный треугольник. По теореме Пифагора найдем половину диагонали основания. Она равна квадратному корню из 21.Диагональ основания и стороны квадрата также представляют собой прямоугольный равнобедренний треугольник. Поэтому по теореме Пифагора найдем сторону квадрата. Сторона равнаквадратный корень из 42. Теперь осталось найти объем пирамиды по формуле: V=1\3 SOCH h. V=1\3 х42х2=28.
Ответ: 28.
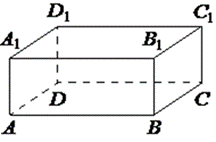
| 2) В прямоугольном параллелепипеде ABCD A1B1C1D1 рёбра DA, DC и диагональ DA1 боковой грани равны соответственно 3, 5 и √34. Найдите объём параллелепипеда ABCDA1B1C1D1. Решение:Это не подобие, это не части, значит, здесь применяется формула объема параллелепипеда и теорема Пифагора. По теореме Пифагора найдем высоту, она равна 5. Объем равен произведению измерений параллелепипеда 5х5х3=75 Ответ: 75 |
|
2) В сосуде, имеющем форму конуса, уровень жидкости достигает 0,5 высоты. Объём сосуда 1600 мл. Чему равен объём налитой жидкости? Ответ дайте в миллилитрах (см. рисунок задачи № 4).
Решение: это подобие. Значит нужно определить k (изменение линейного размера) k=1/2, т.к. уровень жидкости достигает середины высоты. k3=1/8 (речь в задаче об объеме), поэтому объем налитой жидкости 1600:8=200.
Ответ: 200.
3) В сосуде, имеющем форму конуса, налили 25 мл жидкости до половины высоты сосуда. Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?
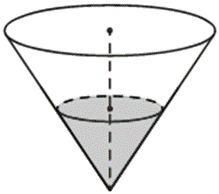
Решение: это подобие, k=1/2, k3=1/8. Объем всего конуса равен 25 х 8 = 200 мл, значит нужно долить 200 – 25= 175 мл.
Ответ: 175.
Примечание: в задачах с применением подобия не нужно записывать формулы обьемов и площадей фигур это только усложняет решение задачи.
|
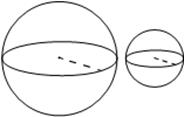
4) Даны два шара с радиусами 4 и 1. Во сколько раз объём большего шара больше объёма меньшего?
Решение: это тоже подобие. k=4, k3=64. Объем большего шара в 64 раза больше меньшего.
Ответ: 64
5) Даны два шара радиусом 6 и 1. Во сколько раз площадь поверхности большого шара больше площади поверхности другого?
Решение: еще одна задача на подобие, но здесь коэффициент нужно возвести в квадрат, т.к. речь идет о площади. k=6, k2=36.
Ответ: 36.
6) Объем данного правильного тетраэдра равен 64 см3. Найдите объем правильного тетраэдра, ребро которого в 2 раза меньше ребра данного тетраэдра.
Решение: это тоже подобие k=2 (одно ребро больше другого в 2 раза), k3=8, 64:8=8 см3 – объем полученного тетраэдра.
Ответ: 8.
|
7) Объем треугольной призмы равен 76. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.
Решение: это не подобие, это части. Объем отсеченной призмы занимает 4 часть от первоначальной призмы. 76:4=19.
Ответ: 19.
8) Найдите объём многогранника, вершинами которого являются вершины A, В, С, A1, В1, С1, правильной шестиугольной призмы
ABCDEFA1 B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11.
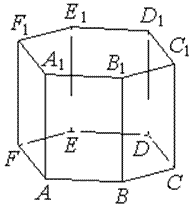
Решение: это не подобие, это части. Многогранник составляет 1/6 часть всей призмы. Объем призмы равен 9х11=99, 99:6=16,5.
Ответ: 16,5.
9) Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.
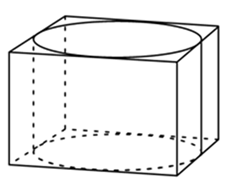
Решение: Это не подобие, это не части, значит, здесь применяется формула объема параллелепипеда. Найдем его измерения: длина равна 4 (два радиуса), ширина равна 4 (два радиуса), высота 2, значит объем равен 4х4х2=32
Ответ: 32.
10) Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса.
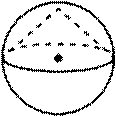
Радиус сферы равен корень из 128. Найдите образующую конуса.
Решение: Это не подобие, это не части, здесь даже нет названия формулы, значит – это теорема Пифагора. Высота конуса (это также и радиус сферы), радиус основания конуса (это также и радиус сферы) и образующая конуса образуют равнобедренный прямоугольный треугольник. По теореме Пифагора образующая равна 16.
Ответ: 16.
Заключение
В данном пособии приведены примеры по двум темам решения заданий ЕГЭ по математике. Но такую систематизацию знаний можно сделать для любых заданий ЕГЭ.
Такая методика особенно актуальна для профильного уровня, где просто работать по алгоритмам решения знакомых задач у ребят не получается. Разнообразие задач так велико, что выучить все задания и их способы решения очень проблематично, принимая во внимание кратковременную память, которая встречается у многих современных школьников, и их информационную загруженность.
Поэтому в современных условиях успешность обучения и его результаты во многом зависят от учителя и его умения дать ученику те несложные инструменты, которые помогут ему при решении незнакомой для него задачи.