Управление образования и науки Липецкой области
ГАУДПО Липецкой области «Институт развития образования»
Методические рекомендации по подготовке обучающихся
К ЕГЭ по математике
Липецк 2019
Методические рекомендации по подготовке обучающихся к ЕГЭ по математике / автор-составитель С.Н. Тархова. – Липецк: ГАУДПО ЛО «ИРО», 2019. – 16 с.
В пособии описана методика решения задач по темам «Применение производной» и «Решение геометрических задач», построенная на алгоритмизации основных способов решения, что позволяет научить обучающихся решать разнообразные задачи с использованием обобщенных алгоритмов.
Введение
В современных школах ежегодно существует проблема качества математического образования. Поставленная руководителями государства и региона задача в отношении повышения качества математического образования является актуальной не только в аспекте наращивания профессионального (кадрового) потенциала для инновационной экономики, но и в аспекте индивидуального и личностного развития каждого школьника, поскольку изучение математики и развитие математической компетентности «станет одним из основных показателей интеллектуального уровня человека, неотъемлемым элементом культуры и воспитанности, будет естественно интегрироваться в общегуманитарную культуру» (Концепция развития математического образования в Российской Федерации).
Задача повышения качества математического образования актуальна не только с позиции «потребностей будущего», но и с позиции актуального состояния математического образования.
По данным исследований первокурсники вузов не приучены ни работать с литературой самостоятельно, ни ориентироваться в незнакомых нешаблонных ситуациях без подсказки опытного учителя. Об этом даже говорит процент решённых на ЕГЭ по математике творческих нетиповых задач. Поэтому вопросы, связанные с подготовкой к ЕГЭ по математике, до сих пор стоят довольно остро.
Учителя математики понимают, что невозможно достичь высоких результатов по сдаче ЕГЭ без системной, долговременной и продуманной работы по подготовке обучающихся.
Задания ЕГЭ рассчитаны на максимальное стимулирование нестандартного мышления при его выполнении. Невольно встает вопрос: «Как подготовить всех детей к успешной сдаче ЕГЭ?». Научить школьника математике и подготовить к успешному написанию ЕГЭ по математике – это две абсолютно разные задачи. Думаю, что это осознает каждый школьный учитель.
Задача учителей – дать равную возможность каждому выпускнику получить качественную подготовку к экзамену по математике, освоить тот объём знаний, умений и навыков, который необходим для успешной сдачи ЕГЭ и профессионального выбора. Обучающиеся, родители, учителя-предметники – все, заинтересованы в получении хороших результатов. Поэтому каждый педагог ищет в своей работе наиболее эффективные формы, методы и технологии обучения.
Данная методика подготовки обучающихся к ЕГЭ по математике создана в ходе анализа личного и опыта коллег использования приемов и методов индивидуальной практико-ориентированной системы обучения. Это – деятельностная технология, в основе которой лежит педагогика понимания, и индивидуальный подход к обучению.
Методика решения задач по теме: «Применение производной»
Рассмотрим решения заданий по теме: «Применение производной». Предложенная тема обусловлена несколькими причинами. Одной из них является невысокий процент решающих задания с производной на диагностических и тренировочных работах, при сдаче ЕГЭ. И, конечно же, интересным аспектом для рассмотрения этой темы стали проблемы с интерпретацией учащимися графиков самой функции, производной и неумением учащихся внимательно «вчитываться» в текст задачи.
Чтобы решить задание № 7 (профильный уровень), конечно, нужно хорошо знать теорию производной функции, но эти знания не всегда помогают учащимся правильно выбрать математическую модель, которую нужно использовать именно при решении этой конкретной задачи. В этом и состоит задача учителя: помочь ученику, разобраться о какой конкретной модели идет речь. Предлагаю Вам посмотреть на некоторые задания из открытого банка заданий по теме «Производная». Внешне эти задания абсолютно не похожи и кажется, что для решения каждой из этих задач существует свой способ решения, но это не совсем так. Здесь всего три принципиально разных математических модели.
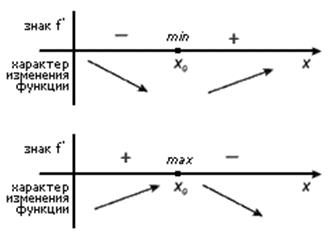
1) Исследование функции (в задаче есть слова возрастание, убывание, экстремумы производная положительна и т.д.) В этом случае строится таблица связи функции и производной. И именно с ее помощью ищется решение.
Физический смысл производной (в задаче идет речь о материальной точке, законе движения, скорости, ускорении). В этом случае нужно взять производную закона движения получится закон скорости, и решать задачу далее по тексту.
3) Геометрический смысл производной (в задаче обязательно присутствует слово касательная). Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох и производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке, f1(х0)=к.
Эти три задачи так отличаются по смыслу, а соответственно и по математической модели, что их невозможно спутать между собой. Обучающийся просто должен знать, когда и какой моделью ему воспользоваться. Давайте более подробно посмотрим на задачи из открытого банка заданий для подготовки к ЕГЭ.
1) На рисунке изображён график функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. В скольких из этих точек производная функции f(x) отрицательна?
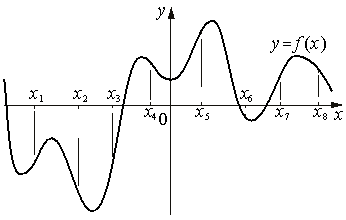
Решение: При решении данной задачи следует применить схему исследования функции с помощью производной. Так как требуется найти точки, в которых функция отрицательна, достаточно указать точки, в которых функция убывает. Это точки х2, х4, х6, х8.
Ответ: 4.
2) На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
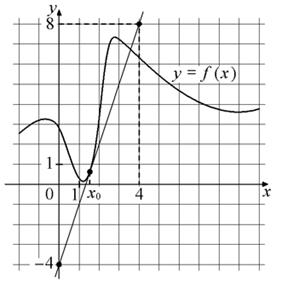
Решение: в условии задачи есть слово «касательная», а это значит, что при решении задания нужно использовать геометрический смысл производной: производная функции в точке равна коэффициенту прямой. Самый простой способ найти коэффициент – построить прямоугольный треугольник прямым углом вниз координата (4; -4), гипотенуза проходит через точки (4; 8) и (0; -4). k=У/Х, k= 12/4=3. Осталось определить знак k, т.к. касательная возрастает, то k больше нуля.
Ответ: 3.
3) На рисунке изображён график y=f′(x), производной функции f(x), определённой на интервале (−9; 8).
Найдите точку экстремума функции f(x) на отрезке [−3; 3].
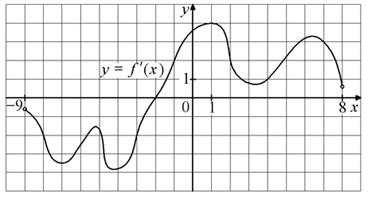
Решение: При решении задачи требуется применить схему исследования функции по ее производной, т.к. в условии есть слово «экстремум». Экстремум - это мах и мin функции. На рисунке изображена производная, а это значит нужно найти точки, в которых она равна нулю - эти точки находятся на оси ОХ, а такая точка только одна.
Ответ: 1.
4) На рисунке изображён график функции y=f(x), определённой на интервале (− 5; 9). Найдите количество точек, в которых производная функции f(x) равна 0.
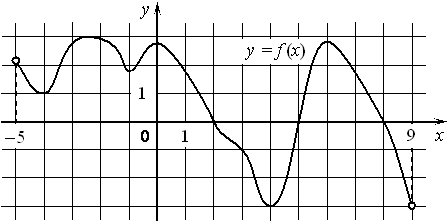
Решение: в задаче есть слова «производная равна 0», а это значит, что применяется схема исследования функции, но в отличи от задачи № 3 на рисунке изображена функция, значит чтобы ответить на вопрос задачи нужно посчить колличество точек мах и мin функции входящих в данный промежуток. Их 6.
Ответ: 6.
Примечание: Особое внимание нужно обратить на промежуток на котором определена функция и о каком промежутке идет речь в вопросе задачи, очень часто они не совпадают.
5) На рисунке изображён график производной функции y=f(x), определённой на интервале (− 5; 9). Найдите количество точек, в которых касательные будут параллельны или совпадать с графиком функций y = -x + 5 (см. рисунок из задачи № 4).
Решение: несмотря на то, что в задании используется тот же рисунок, это задача, на совсем другую схему, т.к. в условии звучит слово «касательная», то это геометрический смысл производной и требуется понять из условия задачи, что k= -1, ведь коэффициент – это число стоящее перед Х в уравнении касательной. Если k= -1, то и производная равна -1, а таких точек на графике 3, поэтому и количество искомых точек равно 3.
Ответ: 3.
6) Материальная точка движется прямолинейно по закону x(t)=12t2+4t+27, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. Найдите её скорость (в метрах в секунду) в момент времени t=2с.
Решение: в решении этой задачи применяется физический смысл производной, т.к. в тексте задания присутствуют слова «материальная точка», «закон движения», «скорость». Скорость есть производная закона движения. Производная данного закона равна 24t+4 и при t=2с скорость будет равна 24х2+4=52.
Ответ:52.
7) Материальная точка движется прямолинейно по закону x(t)=16 t3 − 24t2 + 6t + 250, где x — расстояние от точки отсчёта в метрах, t — время в секундах, измеренное с момента начала движения. В какой момент времени (в секундах) её скорость была равна 6 м/с?
Решение: Здесь также применяется физический смысл производной, поэтому нужно найти производную данного закона движения 48 t2-48t+6 это и есть скорость, осталось только приравнять ее к 6 и решить полученное уравнение. Корень уравнения t1=0 не подходит по условию задачи, а корень t2 =1 и есть ответ на данный вопрос.
Ответ: 1.
8) Прямая y= -6x + 7 является касательной к графику функции
y=ax2 – 2x + 8. Найдите а.
Решение: слово «касательная», которое звучит в условии задачи, указывает на то, что при решении задачи применяется геометрический смысл производной. Производная данной функции равна коэффициенту прямой. Осталось решить уравнение 2ах-2=-6, т.к. уравнение имеет 2 переменные, то требуется наличие 2 уравнения с этими же переменными. Касательная и функция имеют общую точку (это точка касания) поэтому второе уравнение имеет вид –6х+7=ах2-2х+8. Решив систему этих 2 уравнений, получаем, а=4.
Ответ: 4.
9) На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Решение: это геометрический смысл производной (есть слово касательная). Значение производной в точке х0 равно k. Чтобы найти k нужно рассмотреть прямоугольный треугольник с прямым углом вниз и вершинами в точках (-1; 2), (-1; -3), (3; -3) k=У/Х (У=5 просто посчитать клетки вертикального катета; Х=4 посчитать клетки горизонтального катета). k=1,25. Теперь определим знак производной. Так как прямая убывающая, то k отрицательный, а значит производная отрицательная.
Ответ: -1,25.
| 10) На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и значениями их производной в точке x=1. | ||||||||||||||||||||||||
|
В таблице под каждой буквой укажите соответствующий номер.
Решение: это задание № 14 базового уровня, но здесь также применяется геометрический смысл производной.
Графики А) и Б) возрастающие, значит производная положительная – это ответы 1) и 4) Производная это скорость изменения функции, поэтому, чем «круче» прямая, тем больше производная А-1, Б-4. Графики В) и Г) убывающие, поэтому производная отрицательная, на графике Г) процесс убывания происходит более быстро поэтому В-3, Г-2.
Ответ: 1432.
11) На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
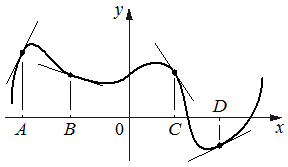В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
| |||||||||||||||||||||||
| |||||||||||||||||||||||
В таблице для каждой точки укажите номер соответствующего значения производной.
Решение: при решении данного задания (базовый уровень) также применяется геометрический смысл производной. Рассуждения в этой задаче аналогичны предыдущему решению. А-3 (график в этой точке более интенсивно возрастает), Д-2 (график возрастает), С-1 (график более интенсивно убывает), В-4.