«Реалити-шоу» точно такое же. Отличие будет в способе интегрирования. Если в интеграле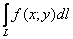 
мы объединяли бесконечно малые кусочки 
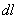самой кривой, то сейчас интегрирование пойдёт по проекциям 
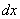этих кусочков на ось абсцисс:
,
или, как вариант – по их проекциям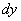 
на ось ординат:
,
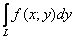и если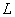 
не параллельна координатным осям, то:
.
В большинстве задач приходится иметь дело с так называемой общей формой криволинейного интеграла от двух функций:
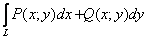
С практической точки зрения будут важнЫте же свойства линейности и аддитивности, а также тот факт, что:
криволинейный интеграл 2-го рода зависит от направления интегрирования, причём:
И в самом деле – здесь же интегрирование осуществляется не по длинам 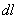(которые беспрекословно положительны), а по их безразмерным проекциям, которые могут быть и отрицательными.
С чисто формальной точки зрения криволинейный интеграл 2-го рода «опознаётся» по наличию в подынтегральном выражении дифференциалов 
(намного реже – какого-то одного), и алгоритм его решения гораздо бесхитростнее, нежели «разборки» со «старшим братом»:
Пример 4
Вычислить криволинейный интеграл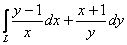 
, где 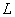– отрезок прямой от точки 
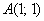до точки 
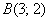. Выполнить чертёж.
Решение: на первом шаге нам нужно найти уравнение прямой, которая содержит отрезок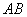 
. Составим его по двум точкам:
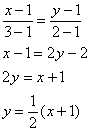
Несмотря на то, что линия интегрирования весьма простА, по условию требуется выполнить чертёж:
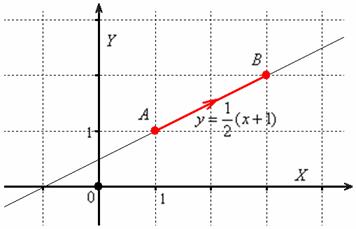
Обязательно указываем направление интегрирования! – здесь оно имеет принципиальное значение. Также обратите внимание на область определения подынтегральных функций – в данном примере 
, и поэтому линия интегрирования не должна пересекать координатные оси! Иногда авторы задачников и методичек недоглядывают за этим моментом, в результате чего получается невразумительное решение, где ответ, например, может оказаться бесконечным. Нет, конечно, мы вправе рассмотреть и несобственный криволинейный интеграл, но обычно задумка совсем не такая.
Криволинейный интеграл 2-го рода тоже сводится к определённому интегралу с «избавлением» либо от всех «игреков», либо от всех «иксов».
Способ первый, традиционный, где осуществляется переход к интегрированию по переменной 
. Пределы интегрирования, как нетрудно догадаться, соответствуют «иксовым» координатам точек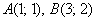 
, при этом не имеет значения, какой из них больше, а какой меньше; НО, принципиально важен порядок – интегрировать нужно строго по заданному направлению: от 1 до 3.
Берём уравнение линии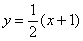 
и находим дифференциал:
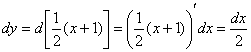
Подставим 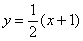и 
в подынтегральное выражение – всё настолько прозрачно, что я даже формулу записывать не буду:
Ответ: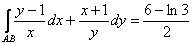 
Если проинтегрировать наоборот – от точки 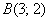до точки 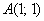, то получится то же самое, только с другим знаком: 
– в силу известного свойства определённого интеграла.
Способ второй состоит в переходе к интегрированию по переменной 
. Для этого из уравнения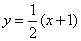 
выразим обратную функцию:
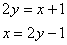
и найдём дифференциал 
.
Перейдём к определённому интегралу от 1 до 2 («игрековые» координаты точек 
и 
), подставив при этом в подынтегральное выражение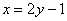 
и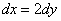 
:
Второй способ оказался технически труднее, но, разумеется, бывает и наоборот. Поэтому перед решением всегда полезно «прикинуть» оба пути. И да – проверка же, не ленИтесь!
Но тут есть исключение: если фрагмент или весь путь интегрирования параллелен координатной оси, то способ остаётся только один! Ибо проекция этого участка на другую ось равна нулю.
Ответ: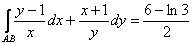
Для самостоятельного решения я всегда стараюсь подбирать наиболее интересные задачи, которые мои студенты всегда выполняют с большим энтузиазмом иначе ни хрена не сдадут:);-)
Пример 5
Вычислить криволинейный интеграл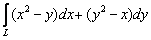 
от точки 
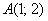до точки 
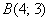вдоль ломаной, состоящей из отрезков прямых 
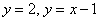. Выполнить чертёж.
Краткое решение и ответ в конце урока.
У многих читателей наверняка назрел вопрос: в чём смысл такого интегрирования? У криволинейных интегралов 2-го рода есть каноничный физический смысл (и не только), с которым мы непременно познакомимся на следующем уроке ( Интегрирование по замкнутому контуру и формула Грина ). Всё будет – и примеры, и пояснения, и ссылки. А пока нарабатываем технические навыки.
Пример 6
Вычислить криволинейный интеграл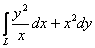 
, где 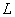– дуга кривой 
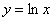от точки 
до точки 
.
Решение: для удобства выполним чертёж, не забывая подметить, что линия интегрирования не может пересекать ось ординат (т.к.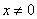 
), впрочем, она здесь заведомо не может – ибо логарифм:
И сейчас я вас познакомлю с ещё одним приёмом решения. По причине той же аддитивности, интеграл можно разделить на две части:
– и с каждым из них разделаться по отдельности:
1) Вычислим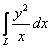 
. Так как 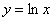, то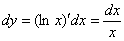 
, изменяется от 1 до 
:
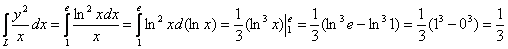
Надеюсь, на данный момент все читатели понимают, как решать интеграл подведением функции под знак дифференциала. Результат, кстати, не помешает проверить интегрированием по «игрек»:
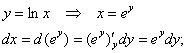
изменяется от 0 до 1 (см. чертёж):
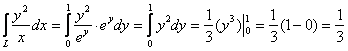, что и требовалось проверить. Напоминаю, что второй путь можно смело выбирать и за основной.
Со второй частью всё проще:
2) 
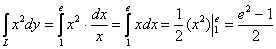
Контроль по «игрек»: 
Осталось просуммировать полученные значения:
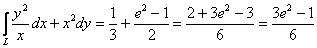
Ответ: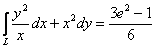 
Разделение интеграла особенно удобно в тех случаях, когда подынтегральное выражение сильно «наворочено». Очередная «бомба» для самостоятельного решения:
Пример 7
Проверить, существует ли интеграл по данной кривой, и вычислить его, если это возможно
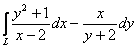– по дуге параболы 
от точки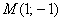 
до начала координат.
Выполнить чертёж.
Вспоминаем, как интегрируются дроби. Краткое решение и ответ в конце урока.
И в заключение урока пара ласковых о параметрически заданной кривой:
Пример 8
Вычислить криволинейный интеграл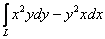 
по кривой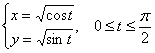 
Решение: чертежа здесь, благо, чертить не требуется, да он и не нужен – условие таково, что снимай данные, да решай.
Как решать? Объясню буквально в 7 словах:)
– в подынтегральном выражении нужно всё выразить через параметр.
При этом во многих случаях, и в этом в частности, «начинку» удобно обработать отдельно. Сначала разбираемся с дифференциалами:
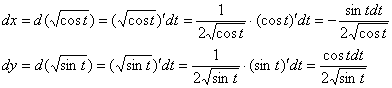
Теперь без спешки и ВНИМАТЕЛЬНО подставляем их вместе с прародителями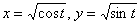 
в подынтегральное выражение, после чего аккуратно проводим упрощения:
И что приятно, тут не нужно думать над пределами изменения параметра:
Ответ: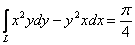 
Самостоятельно:
Пример 9
Вычислить криволинейный интеграл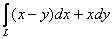 
по верхней половине эллипса 
. Интегрировать против часовой стрелки.
Статья о площади и объёме для параметрически заданной линии в помощь (Пример 2).