Геометрия 8 класс
ТЕМА: Ромб. Квадрат
| Цель деятельности учителя | Создать условия для введения понятий ромба и квадрата как частных видов параллелограмма, для рассмотрения свойств и признаков ромба и квадрата; показать их применение в процессе решения задач | |||
| I этап. Проверка домашнего задания | ||||
| Вспомните. | 1. Дайте определение прямоугольника. Посмотрите начало видео. 2. Перечислите свойства прямоугольника. 3. Перечислите признаки прямоугольника. | |||
| Посмотрите решение задачи | 4. Решите задачу:
б) ∆ АМО = ∆ ВМО по двум катетам (АО = ВО, МО – общая сторона, Ð AOM = Ð MOB = 90°), тогда AM = MB = 6 см и ∆ АМВ – равносторонний. в) Ð AMO = Ð BMO = 30°, так как ∆ АМВ – равносторонний, МО – медиана, высота и биссектриса ∆ АМВ. г) Ð KLM = 90°, Ð AMO = 30°, Ð BMO = 30°, тогда Ð AML = 30°. д) ∆ ALM – прямоугольный, в нем Ð AML = 30°, AM = 6 см, тогда AL = 3 см. е) АK = 6 см, AL = 3 см, тогда KL = 9 см. Ответ: KL = 9 см. | |||
| II этап. Учебно-познавательная деятельность | ||||
| Изучение нового материала. Продолжите смотреть видео. | ||||
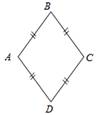
| Ввести понятия ромба | 1. Введение понятия ромба. «Параллелограмм, у которого все стороны равны, называется ромбом» 2. Свойства ромба, признак ромба. Прочитайте п. 47 и – Перечислите все свойства ромба как частного вида параллелограмма. | |||
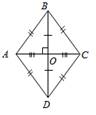
в) Ð А = Ð С, Ð В = Ð D;
г) АО = ОС, ВО = ОD; д) АС ^ ВD. е) АО, ВО, СО, DО – биссектрисы углов A, B, C, D. – Сформулируйте утверждение, обратное особому свойству ромба. 3. Определение квадрата. Прямоугольник у которого все стороны равны называется квадратом.
| ||||
| 4 Запишите в тетрадях: Свойства квадрата: а) AB = BC = CD = AD; AB || CD, ВС || AD; б) Ð А = Ð В = Ð С = Ð D = 90° в) ВО = ОС = ОD = АО, BD ^ АС, АО, ВО, СО, DO – биссектрисы Ð A, Ð B, Ð C, Ð D соответственно. – Найдите в пункте признаки квадрата. | ||||
| Закрепление изученного материала | ||||
| Посмотрите решение задач № 406. | Дано: ABCD – ромб, Ð B = 60°, АС = 10,5 см.
Найти: PАВСD.
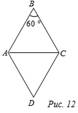Решение:
Ð B = 60°, АВ = ВС (так как АВ и ВС – стороны ромба), тогда Ð BAC = Ð BCA = = 60°, то есть ∆ АВС – равносторонний и АВ = АС = 10,5 см. У ромба все стороны равны, поэтому PАВСD = 4 · АВ = 4 · 10,5 = 42 (см).
Ответ: 42 см.
| |||
| 2. № 407 | Решение: Ð ABC = 45°. BD – диагональ и биссектриса Ð ABC. Ð ABD = 45°: 2 = 22°30' Из ∆ АВО (Ð O = 90°, так как диагонали ромба перпендикулярны): Ð OAB = 90° – 22°30' = 67°30' Ответ: 22°30', 67°30' | |||
| III этап. Итоги урока. Рефлексия | ||||
| – Что нового узнали на уроке? – Какой этап урока оказался для вас самым сложным? – Оцените свою работу на уроке | Домашнее задание: п. 47 прочитать; решить № 412, 413 | |||
Выполните рисунки в тетради
|
|
Мне прислать только дом задание. Или в пятницу вечером или в субботу утром.
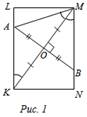
Решите задачу:
Через середину диагонали KМ прямоугольника KLMN перпендикулярно этой диагонали проведена прямая, пересекающая стороны KL и MN в точках А и В соответственно. Известно, что АВ = ВМ = 6. Найдите бо́льшую сторону прямоугольника.
Решите задачи по готовым чертежам:
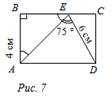
1) ABCD – прямоугольник. Найти: Ð ABF. 2) АСЕK – прямоугольник, ВС = 5 см. Найти: PBDFM
 
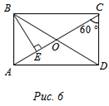
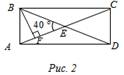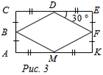3) ABCD – прямоугольник. Доказать: АМ = ND. 4) ABCD – прямоугольник. Найти: Ð АОВ, Ð ВОС.
 
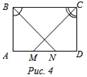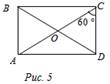5) ABCD – прямоугольник. Найти: АС, АВ. 6) ABCD – прямоугольник. Найти: AD.
 
| 
|