Простой (для ряда динамики с равностоящими уровнями)

Темп (коэффициент) роста характеризует относительную скорость роста или снижения уровней ряда динамики и представляет собой отношение каждого последующего уровня к предыдущему, принятому за базу сравнения. Темп роста измеряется в процентах, а коэффициент роста - в долях.

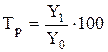(2)

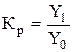(3)

Между цепными и базисными коэффициентами роста существует взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному темпу роста последнего периода; частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.

 

3. Темп (коэффициент) прироста показывает, на сколько процентов изменился сравниваемый уровень по отношению к уровню, принятому за базу сравнения:

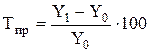(4)

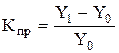(5)

 

4. Абсолютное значение одного процента прироста определяется отношением абсолютного прироста к темпу прироста, и показывает, сколько единиц в абсолютном выражении приходится на один процент прироста для данного ряда динамики. Расчет этого показателя целесообразен для цепного способа, для базисного способа он будет постоянной величиной:

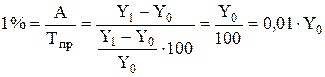(6)

 

Для обобщающей характеристики динамики исследуемого явления за ряд периодов определяют различного рода средние показатели. Существуют две категории этих показателей:

1) средние уровни ряда;

2) средние показатели динамики данного ряда.

Метод расчета среднего уровня динамического ряда зависит от вида временного ряда.

В интервальных рядах динамики из абсолютных уровней средний уровень определяется по формуле средней арифметической:

простой (при равных интервалах):

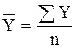(7)

где 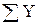- сумма абсолютных уровней ряда;

n - число уровней.

взвешенной (при неравных интервалах):

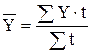(8)

где Y - уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени t;

t - длительность интервалов времени (дней, месяцев) между смежными датами.

 

Для моментного ряда средний уровень определяется с помощью средней хронологической:

простой (для ряда динамики с равностоящими уровнями)

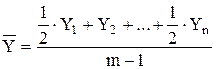(9)

где Y - уровни периода, за который делается расчет;

m - число уровней.

 

взвешенной (для ряда динамики с неравностоящими уровнями):

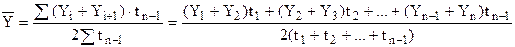(10)

где Y_i, Y_n - уровни ряда динамики;

t - интервал времени между уровнями.

 

ПРИМЕР. Исходя из данных об объёмах производства продукции промышленными предприятиями области необходимо:

1 Определить следующие аналитические показатели ряда динамики цепным и базисным способами: а) абсолютные приросты; б) темпы роста и прироста; в) абсолютное значение 1% прироста.

Результаты расчётов представить в таблице.

2 Проверить взаимосвязь между цепными и базисными абсолютными приростами, темпами роста.

3 Построить график динамики производства продукции промышленными предприятиями области по рассчитанным базисным темпам роста.

4 Проанализировать полученные данные.

Решение:

Построим таблицу 1 "Динамика производства продукции промышленными предприятиями области за 1993-2002 гг."

Таблица 1 - Динамика производства продукции промышленными предприятиями области за 1993-2002 гг.

ГГод	Объём производства продукции, млн. руб.	Абсолютный прирост, млн. руб.	Темп роста,%	Темп прироста,%	Абсолютное значение 1% прироста, млн. руб.
базисный	цепной	базисный	цепной	базисный	цепной
	10,0	-	-			-	-	-
	10,7	0,7	0,7					0,1
	12,0	2,0	1,3		112,1		12,1	0,107
	10,3	0,3	-1,7		85,8		-14,2	0,12
	12,9	2,9	2,6		125,2		25,2	0,103
	16,3	6,3	3,4	126,3	126,4	26,3	26,4	0,129
	15,6	5,6	-0,7		95,7		-4,3	0,163
	17,8	7,8	2,2		114,1		14,1	0,156
	18,0	8,0	0,2		101,1		1,1	0,178
	18,7	8,7	0,7		103,9		3,9	0,18

 

Рассчитаем средний уровень динамики ряда по формуле (7):

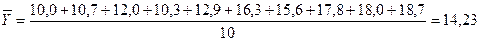(млн. руб.)

 

Проверим взаимосвязь между цепными и базисными абсолютными приростами и темпами роста:

между абсолютными приростами:

А_94/93 + А_95/94 + А_96/95 + А_97/96 + А_98/97 + А_99/98 + А_00/99 + А_01/00 + А_02/01 = =А_02/93

0,7 + 1,3 - 1,7 + 2,6 + 3,4 - 0,7 + 2,2 +0,2 + 0,7 = 8,7 (млн. руб.)

8,7 = 8,7 (млн. руб.)

между темпами роста:

а) k_94/93 · k_95/94 · … · k_02/01 = k_р02/93

1,07 · 1,121 · 0,858 · 1,252 · 1,264 · 0,95 · 1,141 · 1,011 · 1,039 = 1,87%

1,87 = 1,87

б) Например, k 1995:

%

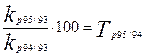
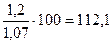112,1 = 112,1.

Построим график динамики производства продукции по рассчитанным базисным темпам роста:

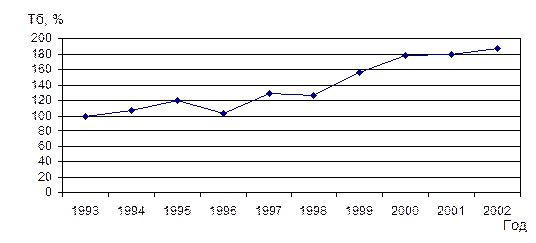
Рисунок 1 - График динамики производства продукции промышленными предприятиями области по рассчитанным базисным темпам роста.

 

Вывод. Проанализировав рисунок 1, можно сделать вывод о том, что наблюдается тенденция к росту производства продукции, в основном. Однако, в 1996 и 1998 годах наблюдался спад производства. В среднем за период с 1993 по 2002 годы объём производства за год составил 14,23 млн. руб., увеличился за отчётный период на 0,97 млн. руб. (средний абсолютный прирост) и составил 7,2% (средний темп роста).0,13 млн. руб. составили 1% прироста в среднем.

 

 

ЗАДАНИЕ.

1. Законспектировать теоретический материал.

2. Решить задачу и сформулировать выводы.

Имеются данные о товарных остатках на 1-е число каждого месяца 1 квартала,

тыс. руб.:

 

01.01.2012	01.02.2012	01.03.2012	01.04.2012
18,0	14,0	16,0	20,0

 

Рассчитать:

· среднемесячный товарный остаток за 1 квартал;

· абсолютный прирост (базисный и цепной);

· темп роста (базисный и цепной);

· темп прироста (базисный и цепной).