1. Дано: 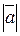 =3,
=3,  =8. Найти векторное произведение
=8. Найти векторное произведение  , если угол φ между векторами равен:
, если угол φ между векторами равен:
1) 0; 2) 30о; 3) 90о; 4) 120о; 5) 150о.
2. Упростить выражения:
1)  ;
2) ;
2) 
| 1)  ;
2) ;
2) 
|
3. Найти векторное произведение для следующих пар векторов:
1)  ;
2) ;
2)  ; ;
| 3)  ;
2) ;
2)  . .
|
4. Найти вектор  , если
, если
1) 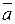 = 2 = 2  ; ; 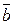 =3 =3  ;
2) ;
2) 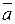 = =  + +  ; ; 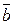 = =  − 2 − 2  ; ;
| 1) 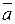 =3 =3  + +  ; ; 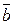 = =  +4 +4  ;
2) ;
2) 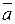 = – = –  + +  + +  ; ; 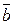 = =  +2 +2  . .
|
Вычислить в каждом случае площадь параллелограмма, построенного на векторах  .
.
5. Вычислить площадь треугольника с вершинами:
1) А (2; 2; 2); В (1; 3; 3); С (3; 4; 2);
2) А (– 3; – 2; – 4); В (– 1; – 4; – 7); С (1; – 2; 2);
6. Найти орт  , перпендикулярный векторам:
, перпендикулярный векторам:
1)  ; 2)
; 2)  ;
;
7. Дан треугольник с вершинами А (9; – 9; 13); В (7; – 13; 17); С (17; – 3; 17). Найти длину высоты, проведенной из вершины С.
8. Дано: 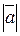 =5,
=5,  =2,
=2,  =6. Найти
=6. Найти  .
.
9. Дано: 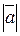 =10,
=10,  =2,
=2,  =16. Найти
=16. Найти  .
.
Смешанное произведение векторов.
1. Найти смешанное произведение векторов 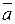
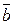
 , если:
, если:
1) 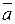 =(1; 1; 2); =(1; 1; 2); 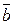 =(1; –2; 3); =(1; –2; 3);  =(2; 1; 1);
2) =(2; 1; 1);
2) 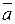 =(5;– 2; –1); =(5;– 2; –1); 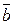 =(1; –2; 1); =(1; –2; 1);  =(1; 2; – 2); =(1; 2; – 2);
| 3) 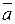 =(1; 1; 4); =(1; 1; 4); 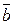 =(2; –1; – 1); =(2; –1; – 1);  =(1; 3; –1). =(1; 3; –1).
|
2. Доказать, что векторы компланарны, если:
1) 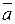 =(1; 1; 3); =(1; 1; 3); 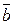 =(0; 2; – 1); =(0; 2; – 1);  =(1; – 1; 4);
2) =(1; – 1; 4);
2) 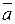 =(1; 2; 2); =(1; 2; 2); 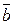 =(2; 5; 7); =(2; 5; 7);  =(1; 1; –1); =(1; 1; –1);
| 3) 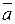 =(1; – 1; 2); =(1; – 1; 2); 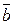 =(3; 5; 0); =(3; 5; 0);  =(5; 3; 4). =(5; 3; 4).
|
3. Вычислить объем тетраэдра с вершинами в точках
1) А (–1; 1; 0); В (2; – 2; 1); С (3; 1; –1); D (1; 0; –2);
2) А (–4; – 4; – 3); В (– 2; –1; 1); С (2; – 2; –1); D (– 1; 3; –2)
4. Показать, что точки А (3; 5; – 4); В (1; –1; – 3); С (7; 2; –6); D (– 1; 3; –2)
принадлежат одной плоскости.
5. Вычислить объем параллелепипеда, построенного на векторах 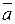 =(3; 2; 1);
=(3; 2; 1); 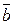 =(1; 0; – 1);
=(1; 0; – 1);  =(1; –2; 1);
=(1; –2; 1);
Линейные пространства.
1. Выяснить, являются ли векторы а 1, а 2, а 3 линейно зависимыми:
1) а 1= (2; −1; 3), а 2 = (1; 4; −1), а 3= (0; −9; 5);
2) а 1= (1; 2; 0), а 2 = (3; −1; 1), а 3= (0; 1; 1).
2. Показать, что векторы а 1= (8; 5; 9; 1), а 2 = (1; −3; –6; –3), а 3= (3; –1; 5; 2), а 4= (0; 2; –1; 4), заданные в базисе е 1, е 2, е 3, сами образуют базис.
|
|
3. Даны векторы а = е 1 + е 2 + е 3, b =2 е 2 + 3 е 3, c = е 2 + 5 е 3, где е 1, е 2, е 3 базис линейного пространства. Доказать, что векторы a, b, c образуют базис. Найти координаты вектора d = 2 е 1 − е 2 + е 3 в базисе a, b, c.
4. Даны векторы а 1, а 2, а 3, b. Показать, что векторы а 1, а 2, а 3 образуют базис трехмерного пространства, и найти координаты вектора b в этом базисе, если:
1) а 1= (4; 3; 2), а 2 = (−3; 2; −1), а 3 = (2; 3; 1), b =(16; 8; 7);
2) а 1= (−1; 2; 0), а 2 = (2; 4; 2), а 3 = (−3; −1; 3), b =(−8; 0; 4).
5. Даны векторы а 1, а 2, а 3, а 4, b. Показать, что векторы а 1, а 2, а 3, а 4 образуют базис четырехмерного пространства, и найти координаты вектора b в этом базисе, если:
1) а 1=(–1; 2; 3; 1), а 2=(–1; 3;−2; –1), а 3=(3; 5; 4; 1), а 4=(3;1;4;–1), b =(0; 3; 5; 4);
2) а 1=(1; 2; 1; 3), а 2 =(1;–1;–1;–1), а 3=(–1; 3; 0;1), а 4 =(1;– 2; 2;–1), b =(4; 1; 6; 0).
Индивидуальное задание №2 по теме: « Элементы векторной алгебры »
Задание №1. Даны координаты вершин пирамиды ABCD. Требуется:
1. Записать векторы 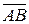 ,
,  ,
,  в системе орт
в системе орт  ,
,  ,
,  и найти модули этих векторов;
и найти модули этих векторов;
2. Найти угол между векторами 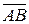 и
и  ;
;
3. Найти проекцию вектора  на вектор
на вектор  ;
;
4. Найти площадь грани АВС;
5. Найти объем пирамиды АВСD.
1) А(1; 2; 1), В(– 1; 5; 1), С(– 1; 2; 7), D (1; 5; 9).
2) А(2; 3; 2), В(0; 6; 2), С(0; 3; 8), D (2; 6; 10).
3) А(0; 3; 2), В(–2; 6; 2), С(– 2; 3; 8), D (0; 6; 10).
4) А(2; 1; 2), В(0; 4; 2), С(0; 1; 8), D (2; 4; 10).
5) А(2; 3; 0), В(0; 6; 0), С(0; 3; 6), D (2; 6; 8).
6) А(2; 2; 1), В(0; 5; 1), С(0; 2; 7), D (2; 5; 9).
7) А(1; 3; 1), В(– 1; 6; 1), С(– 1; 3; 7), D (1; 6; 9).
8) А(1; 2; 2), В(– 1; 5; 2), С(– 1; 2; 8), D (1; 5; 10).
9) А(2; 3; 1), В(0; 6; 1), С(0; 3; 7), D (2; 6; 9).
10) А(2; 2; 2), В(0; 5; 2), С(0; 2; 8), D (2; 5; 10).
11) А(1; 3; 2), В(– 1; 6; 2), С(– 1; 3; 8), D (1; 6; 10).
12) А(0; 1; 2), В(– 2; 4; 2), С(– 2; 1; 8), D (0; 4; 10).
13) А(0; 3; 0), В(– 2; 6; 0), С(– 2; 3; 6), D (0; 6; 8).
14) А(2; 1; 0), В(0; 4; 0), С(0; 1; 6), D (2; 4; 8).
|
|
15) А(0; 2; 1), В(– 2; 5; 1), С(– 2; 2; 7), D (0; 5; 9).
16) А(1; 1; 1), В(– 1; 4; 1), С(– 1; 1; 7), D (1; 4; 9).
17) А(1; 2; 0), В(– 1; 5; 0), С(– 1; 2; 6), D (1; 5; 8).
18) А(0; 1; 0), В(– 2; 4; 0), С(– 2; 1; 6), D (0; 4; 8).
19) А(0; 1; 1), В(– 2; 4; 1), С(– 2; 1; 7), D (1; 4; 9).
20) А(0; 2; 0), В(– 2; 5; 0), С(– 2; 2; 6), D (0; 5; 8).
21) А(4; 2; 5), В(0; 7; 2), С(0; 2; 7), D (1; 5; 0).
22) А(4; 4; 10), В(4; 10; 2), С(2; 8; 4), D (9; 6; 4).
23) А(4; 6; 5), В(6; 9; 4), С(2; 10; 10), D (7; 5; 9).
24) А(3; 5; 4), В(8; 7; 4), С(5; 10; 4), D (4; 7; 8).
25) А(10; 6; 6), В(– 2; 8; 2), С(6; 8; 9), D (7; 10; 3).
26) А(1; 8; 2), В(5; 2; 6), С(5; 7; 4), D (4; 10; 9).
27) А(6; 6; 5), В(4; 9; 5), С(4; 6; 11), D (6; 9; 3).
28) А(7; 2; 2), В(5; 7; 7), С(5; 3; 1), D (2; 3; 7).
29) А(8; 6; 4), В(10; 5; 5), С(5; 6; 8), D (8; 10; 7).
30) А(7; 7; 3), В(6; 5; 8), С(3; 5; 8), D (8; 4; 1).
Задание №2 Даны векторы  ,
,  ,
,  ,
,  . Показать, что векторы
. Показать, что векторы  ,
,  ,
,  образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора  в этом базисе.
в этом базисе.
1)  =(2;1;3),
=(2;1;3),  =(3; −2;1),
=(3; −2;1),  =(1; −3; −4),
=(1; −3; −4),  =(7;0;7).
=(7;0;7).
2)  =(5;3;1),
=(5;3;1),  =(−2; −1;2),
=(−2; −1;2),  =(−2;1; 4),
=(−2;1; 4),  =(3;0;1).
=(3;0;1).
3)  =(1;3;5),
=(1;3;5),  =(−2;−1;−1),
=(−2;−1;−1),  =(4; −2;4),
=(4; −2;4),  =(−7;3;−1).
=(−7;3;−1).
4)  =(3;1;6),
=(3;1;6),  =(−2; 2;−3),
=(−2; 2;−3),  =(−4; 5; −1),
=(−4; 5; −1),  =(3;0;1).
=(3;0;1).
5)  =(4;1;4),
=(4;1;4),  =(−2; −1;1),
=(−2; −1;1),  =(3;1; 5),
=(3;1; 5),  =(− 3;−2;1).
=(− 3;−2;1).
6)  =(1;2;5),
=(1;2;5),  =(2; −3;4),
=(2; −3;4),  =(1; −1; −2),
=(1; −1; −2),  =(3;0;1).
=(3;0;1).
7)  =(5;1;2),
=(5;1;2),  =(3; 4;−1),
=(3; 4;−1),  =(−4; 2; 1),
=(−4; 2; 1),  =(−3;5;4).
=(−3;5;4).
8)  =(2;1;5),
=(2;1;5),  =(−4; 3;5),
=(−4; 3;5),  =(1; −1; −4),
=(1; −1; −4),  =(4;−1;−3).
=(4;−1;−3).
9)  =(3;1;4),
=(3;1;4),  =(−4;2;3),
=(−4;2;3),  =(2;−1;−2),
=(2;−1;−2),  =(7;−1;0).
=(7;−1;0).
10)  =(1;4;2),
=(1;4;2),  =(5;−2;−3),
=(5;−2;−3),  =(−2;−1;1),
=(−2;−1;1),  =(−3;2;4).
=(−3;2;4).
11)  =(1;3;1),
=(1;3;1),  =(1; 2;−1),
=(1; 2;−1),  =(−3; 2;5),
=(−3; 2;5),  =(0;−1;−2).
=(0;−1;−2).
12)  =(3;1;5),
=(3;1;5),  =(−2;3;−2),
=(−2;3;−2),  =(−1; 2; 4),
=(−1; 2; 4),  =(−5;2;−7).
=(−5;2;−7).
13)  =(2;1;4),
=(2;1;4),  =(3; 1;5),
=(3; 1;5),  =(1; −4;−3),
=(1; −4;−3),  =(1;0;1).
=(1;0;1).
14)  =(1;4;2),
=(1;4;2),  =(−4; 1;3),
=(−4; 1;3),  =(2;−3;4),
=(2;−3;4),  =(−5;−3;1).
=(−5;−3;1).
15)  =(2;1;3),
=(2;1;3),  =(4; 1;−2),
=(4; 1;−2),  =(−3;2;1),
=(−3;2;1),  =(2;0;−5).
=(2;0;−5).
16)  =(1;2;4),
=(1;2;4),  =(2; −3;1),
=(2; −3;1),  =(−3; −1; −2),
=(−3; −1; −2),  =(1;−7;0).
=(1;−7;0).
17)  =(3;1;5),
=(3;1;5),  =(−1; 2;3),
=(−1; 2;3),  =(4; 3; 2),
=(4; 3; 2),  =(2;7;8).
=(2;7;8).
18)  =(3;2;1),
=(3;2;1),  =(−3;1;−2),
=(−3;1;−2),  =(2;3;5),
=(2;3;5),  =(−4;−1;1).
=(−4;−1;1).
19)  =(4;3;2),
=(4;3;2),  =(−1; 2;−2),
=(−1; 2;−2),  =(3;4;4),
=(3;4;4),  =(1;8;0).
=(1;8;0).
20)  =(2;1;4),
=(2;1;4),  =(−1;−2;3),
=(−1;−2;3),  =(3; −5; −2),
=(3; −5; −2),  =(1;−9;4).
=(1;−9;4).
21)  =(5;1;2),
=(5;1;2),  =(8;2;−3),
=(8;2;−3),  =(−1;3;2),
=(−1;3;2),  =(−7;1;9).
=(−7;1;9).
|
|
22)  =(1;3;2),
=(1;3;2),  =(2; −5;7),
=(2; −5;7),  =(1;3;−1),
=(1;3;−1),  =(4;1;8).
=(4;1;8).
23)  =(3;2;2),
=(3;2;2),  =(2;3;1),
=(2;3;1),  =(1; 1; 3),
=(1; 1; 3),  =(5;1;11).
=(5;1;11).
24)  =(1;5;3),
=(1;5;3),  =(2;1;−1),
=(2;1;−1),  =(4;2;1),
=(4;2;1),  =(31;29;10).
=(31;29;10).
25)  =(4;2;5),
=(4;2;5),  =(−3;5;6),
=(−3;5;6),  =(2;−3;−2),
=(2;−3;−2),  =(9;4;18).
=(9;4;18).
26)  =(2;3;3),
=(2;3;3),  =(−1;4;−2),
=(−1;4;−2),  =(−1;−2;4),
=(−1;−2;4),  =(4;11;11).
=(4;11;11).
27)  =(1;2;4),
=(1;2;4),  =(1;−1;1),
=(1;−1;1),  =(2;2;4),
=(2;2;4),  =(−1;−4;−2).
=(−1;−4;−2).
28)  =(3;−2;2),
=(3;−2;2),  =(−1;1;−1),
=(−1;1;−1),  =(0;1;4),
=(0;1;4),  =(5;0;15).
=(5;0;15).
29)  =(3;2;1),
=(3;2;1),  =(−1;−5;1),
=(−1;−5;1),  =(1;−3;−1),
=(1;−3;−1),  =(4;−17;0).
=(4;−17;0).
30)  =(1;2;3),
=(1;2;3),  =(1;−1;−2),
=(1;−1;−2),  =(1;−6;0),
=(1;−6;0),  =(−1;8;3).
=(−1;8;3).
§11. Линейные преобразования, §12. Квадратичные формы.
1. В пространстве R2 линейное преобразование задано матрицей  в базисе
в базисе  ,
,  .
.
Найти образ  вектора
вектора  = 4
= 4  – 3
– 3 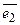 .
.
2. В пространстве R2 линейное преобразование задано матрицей  в базисе
в базисе  ,
,  .
.
Найти образ  вектора
вектора  = 3
= 3  +5
+5 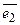 .
.
3. В пространстве R3 линейное преобразование задано матрицей  в базисе
в базисе  ,
,  ,
, 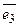 .
.
Найти образ  вектора
вектора  = 2
= 2  +4
+4  –
–  .
.
4. В пространстве R3 линейное преобразование задано матрицей  в базисе
в базисе  ,
,  ,
, 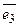 .
.
Найти образ  вектора
вектора  = 3
= 3  – 2
– 2 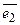 +
+ 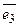 .
.
5. Найти собственные значения и собственные векторы линейного преобразования с матрицей A = 
6. Найти собственные значения и собственные векторы линейного преобразования с матрицей A = 
7. Найти собственные значения и собственные векторы линейного преобразования A, матрица линейного преобразования A =  .
.
8. Квадратичную форму записать в матричном виде:
1)  ; 3)
; 3) 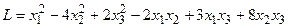
2)  ;
;
9. Исследовать на знакоопределенность и привести к каноническому виду квадратичные формы:
1)  ; 3)
; 3)  ;
;
2)  ; 4)
; 4) 
III. Аналитическая геометрия.