Поверхности 2-го порядка.

Эллипсоид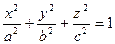

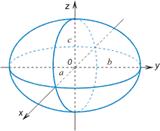
При фиксировании любой переменной получится уравнение эллипса. Любое его сечение - эллипс. Полуоси a,b,c.

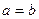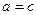Если пара полуосей совпадает, т.е. или или 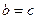, то эллипсоид вращения (сечения вдоль какой-то из плоскостей - круги а не эллипсы). Если же все 3 равны 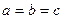, то сфера .

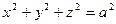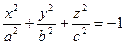- пустое множество (ни одна точка пространства не удовлетворяет этому уравнению).

Однополостный гиперболоид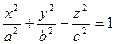

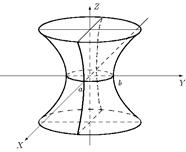
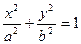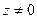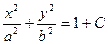При z=0 сечение есть эллипс . Если фиксировать , то эллипс большего размера, но с тем же самым соотношением полуосей.

В вертикальных сечениях будут гиперболы: если фиксировать y, то уравнение сводится к виду, где разность квадратов.

Например, при y = 0: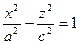

 

Докажем, что однополостный гиперболоид 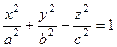содержит прямолинейные образующие.

В горизонтальном сечении при 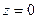получается эллипс: 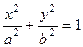. Его вершины: 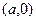, , 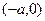, 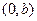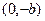. Рассмотрим вертикальную плоскость, проходящую через его вершину, например, 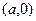. Эта плоскость имеет уравнение 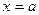. Тогда в уравнении гиперболоида 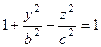, т.е. 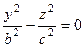. Получается 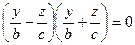, т.е. в вертикальной плоскости две прямых:

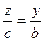и 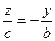, или можно записать так: 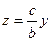и .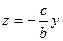

Это пара пересекающихся прямых.

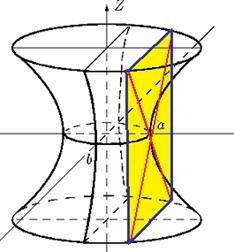
Двуполостный гиперболоид .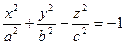

 

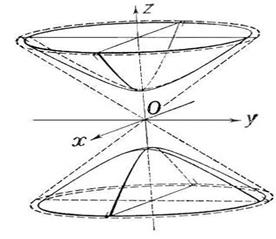
В отличие от прошлого случая, здесь при малых z, по модулю меньших, чем c, вообще пустое множество в горизонтальных сечениях: 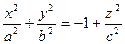здесь только при 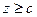справа положительное число и в сечениях эллипсы. Поэтому фигура распадается на 2 части, вблизи начала координат вообще нет точек.

Вертикальные сечения - гиперболы.

Кстати, если вращать гиперболу, расположенную в одних четвертях, то получится 1-полостный гиперболоид, а если вращать гиперболу, которая была в других двух четвертях - 2-полостный гиперболоид:

 

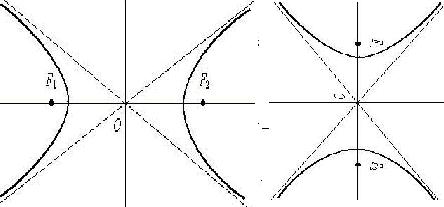
Рассмотрим теперь две поверхности, в уравнениях которых содержится не 3, а 2 квадрата, и первая степень третьей переменной.

 

Эллиптический параболоид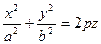

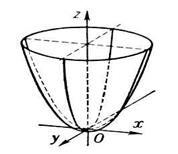
Горизонтальные сечения - эллипсы: если фиксировать z, то получим 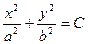.Вертикальные сечения - параболы, ветви которых направлены вверх: если фиксировать например y, то получим

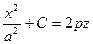уравнение параболы. Параболические антенны построены именно с помощью такой поверхности, но 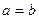(параболоид вращения).

 

Гиперболический параболоид .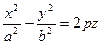

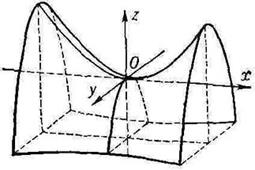
Вертикальные сечения - параболы. Причём если фиксировать x, то сечение в плоскости 0yz - парабола, ветви которой направлены вниз 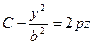, а если фиксировать y, то ветви вверх: .

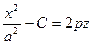В горизонтальных сечениях - гиперболы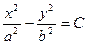

в зависимости от знака z, они то в одних, то в других четвертях.

Можно представить построение этой поверхности так: парабола, ветвями направленная вниз, повернута перпендикулярно и скользит своей вершиной по параболе, направленной ветвями вверх.

Общий случай.

В уравнении поверхности присутствует квадратичная форма .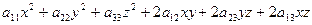

Построить её матрицу (см. прошлую тему), найти собственные числа: 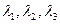. Возможны такие ситуации:

Если они все одного знака (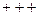), то поверхность - эллипсоид.

Если два из них одного знака, а третье другого знака (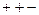) гиперболоиды.

Если одно из них 0, а другие одного знака (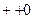) эллиптический параболоид.

Если одно из них 0, а другие разного знака (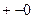) гиперболический параболоид.

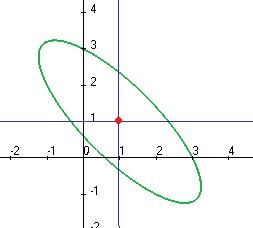
Задача 141. Доказать, что кривая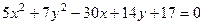

является эллипсом, найти каноническое уравнение, центр и полуоси.

Решение. Выделим полный квадрат по каждой переменной.

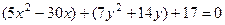
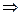
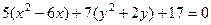в каждой скобке можно получить такое выражение, чтобы затем использовать формулы сокращённого умножения (ФСУ): 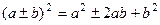. Надо прибавить константы в скобках, так чтобы всё сворачивалось, но для компенсации за скобками вычесть эти константы.

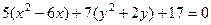
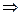
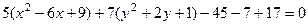
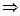
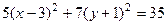
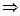
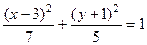
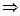
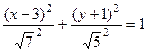это каноническое уравнение.

Ответ. Центр 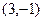, полуос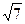и и .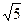

Чертёж:

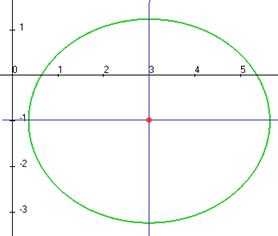
Задача 142. Доказать, что кривая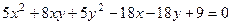

является эллипсом, найти каноническое уравнение, центр и полуоси, построить чертёж.

Решение. Здесь в уравнении есть произведение 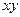, то есть надо сначала привести к главным осям квадратичную форму: 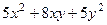. Строим её матрицу: .

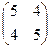Находим собственные числа и векторы.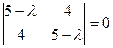

.

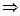
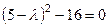
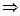
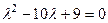
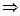
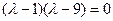Собственные числа 1 и 9. Ищем собственные векторы.

 

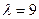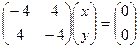. , оба уравнения пропорциональны, т.е. есть только такая информация: 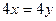, т.е. 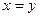. ФСР: вектор (1,1).

Нормируем его, то есть делим на длину, которая здесь 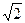. Получаем

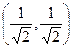- собственный вектор для .

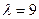Это единичный вектор в 1-й четверти, получающийся поворотом (1,0) на 45 градусов.

 

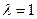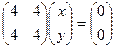. , оба уравнения пропорциональны, фактически оно одно: 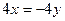, т.е. 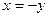. ФСР: вектор .

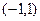Нормируем его, получаем 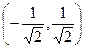собственный вектор для .

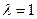Это вектор во 2-й четверти, получающийся поворотом (0,1) на 45 градусов.

Запишем формулы перехода от одного базиса к другому:

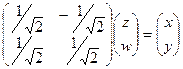
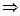
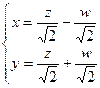
Если подставить эти выражения в исходное уравнение, то после приведения подобных исчезнут выражения, содержащие разные переменные 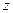и :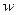

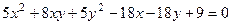
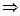
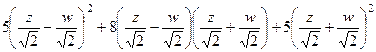
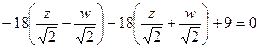
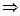
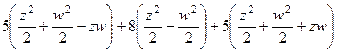
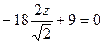
в линейной форме 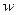полностью сократились, 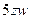тоже сократятся.

.

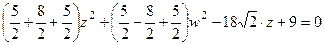
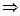
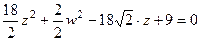
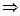
Итак, как мы видим, коэффициентами как раз и оказались 9 и 1, то есть собственные числа матрицы этой квадратичной формы.

Заметим, что 1-й степени 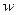здесь нет, так что выделение полного квадрата надо делать только по .

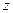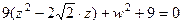
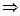
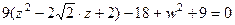
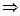
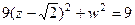
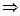
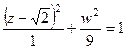, т.е. 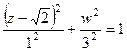. Полуоси 1 и 3, то есть размеры эллипса: 2 на 6.

Центр 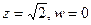, но это центр в новых координатах, а для чертежа надо найти центр именно в старых координатах 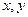. Их мы найдём по формулам взаимосвязи этих координат:

.

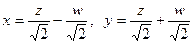Если 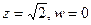, то .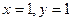

Итак, центр - точка (1,1). В направлении первого вектора нового базиса, а именно 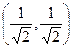, полуось длины 1, а в направлении второго вектора 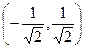полуось длины 3.

Ответ. Центр 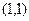, полуоси 1 и 3.

Чертёж: