Основные операции над множествами
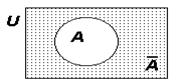
1) Дополнение: 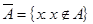 Дополнение множества A - множество, состоящее из всех элементов универсума, не принадлежащих A.
Дополнение множества A - множество, состоящее из всех элементов универсума, не принадлежащих A.
| 
|
2) Пересечение: 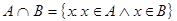 Пересечение множеств A и B - множество, состоящее из всех элементов, принадлежащих одновременно и A, и B.
Пересечение множеств A и B - множество, состоящее из всех элементов, принадлежащих одновременно и A, и B.
| 
|
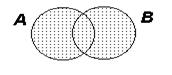
3) объединение: 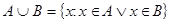 Объединение множеств A и B - множество, состоящее из элементов, принадлежащих хотя бы одному из указанных множеств.
Объединение множеств A и B - множество, состоящее из элементов, принадлежащих хотя бы одному из указанных множеств.
| 
|
4) Дизъюнктивная сумма (симметрическая разность):
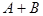 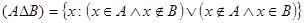 Дизъюнктивная сумма множеств A и B - это множество, состоящее из элементов, принадлежащих либо только A, либо только B.
Дизъюнктивная сумма множеств A и B - это множество, состоящее из элементов, принадлежащих либо только A, либо только B.
| 
|
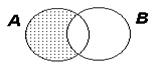
5) Разность:  Разность множеств A и B - это множество, состоящее из элементов, принадлежащих A, но не принадлежащих B.
Разность множеств A и B - это множество, состоящее из элементов, принадлежащих A, но не принадлежащих B.
| 
|
Свойства операций над множествами
Операции над множествами, сформулированные в (1.4) обладают некоторыми свойствами, приведенными в табл. 1. Эти свойства выражаются совокупностью тождеств, справедливых независимо от конкретного содержания входящих в них множеств, являющихся подмножествами некоторого универсума U.
Таблица 1
Основные свойства операций над множествами
1а) 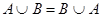
| 1б) 
|
2а) 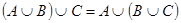
| 2б) 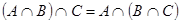
|
3а) 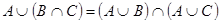
| 3б) 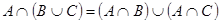
|
4а) 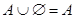
| 4б) 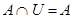
|
5а) 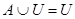
| 5б) 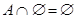
|
6а) 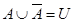
| 6б) 
|
7а) 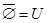
| 7б) 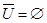
|
8а) 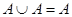
| 8б) 
|
9а) 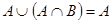
| 9б) 
|
10а) 
| 10б) 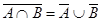
|
11) 
| |
12) 
| |
13) 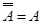 - закон двойного отрицания - закон двойного отрицания
| |
14) 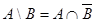
| |
15) 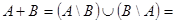 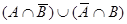
| |
16) 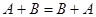
| |
| 17) (А + В) + С = А + (В + С) | |
| 18) А + Æ = Æ + А | |
19) 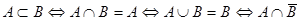 =Æ =Æ
| |
20) 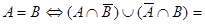 Æ Æ
|
Тождества (1а)-(3а) выражают соответственно коммутативный, ассоциативный и дистрибутивный законы для объединения, а тождества (1б)-(3б) - те же законы для пересечения. Соотношения (4а)-(7а) определяют свойства пустого множества Æ и универсума U относительно объединения, а соотношения (4б)-(7б) - относительно пересечения.
Выражения (8а) и (8б), называемые законами идемпотентности, позволяют записывать формулы с множествами без коэффициентов и показателей степени. Зависимости (9а) и (9б) представляют законы поглощения, а (10а) и (10б) - законы де Моргана.
Соотношения (11)-(20) отражают свойства дополнения, разности, дизъюнктивной суммы, включения и равенства.
Первые десять свойств в табл. 1 представлены парами двойственных (дуальных) соотношений, одно из которых получается заменой в другом символов: È на Ç и Ç на È, а также Æ на U и U на Æ. Соответствующие пары символов È, Ç и Æ, U называются двойственными (дуальными) символами.
При замене в любой теореме входящих в нее символов дуальными получим новое предложение, которое также является теоремой (принцип двойственности или дуальности). Тождество (11) не изменяется при замене символов дуальными, поэтому его называют самодвойственным.
Декартово произведение множеств
Декартово произведение множеств A и B – это множество упорядоченных пар, первый элемент которых принадлежит A, а второй – принадлежит B.

Пример. 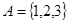
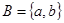

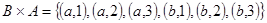
Свойства декартова произведения:
1) 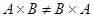 - некоммутативность
- некоммутативность
2)  =
= 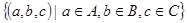 - ассоциативность
- ассоциативность
Свойство ассоциативности позволяет использовать сокращенную запись для декартова произведения нескольких множеств:

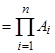
3)  - дистрибутивность относительно объединения
- дистрибутивность относительно объединения
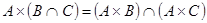 - дистрибутивность относительно пересечения
- дистрибутивность относительно пересечения
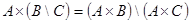 - дистрибутивность относительно разности
- дистрибутивность относительно разности
Доказательство: Докажем, например, дистрибутивность декартова произведения относительно операции пересечения множеств.
1) 
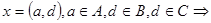
 ;
; 
2)  ,
, 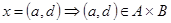 ,
, 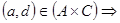

Особым случаем декартова произведения является произведение множества самого на себя. В этом случае говорят о декартовом квадрате множества или декартовой n-ой степени множества А.
 ;
; 
Пример.  Þ
Þ 
Теорема. Если множество A содержит n элементов, а B – m элементов, т.е.: 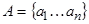
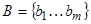 , то
, то 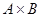 содержит
содержит 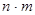 элементов.
элементов.