Логические схемы – это графические модели, предназначенные для оценки времен-
ных характеристик информационных процессов: времени завершения (при детерминированной модели), среднего времени и дисперсии времени завершения процесса (при вероятностных моделях, содержащих элементы неопределенности) [2.1].
При оценке временных характеристик несущественны сведения о том, где, когда и с помощью каких средств реализуется та или иная операция. Зато необходимо знать характеристики длительности выполнения операции и правила, определяющие характер их следования.
Для представления информационных процессов с целью оцениванияих временных характеристик используются модели с символикой, показанной в табл. П1.1. Приложения 1. Приведенная в табл. П1.1 система графических символов, в основном, следует [2.5].
Последовательность действий при использовании аппарата логических схем для расчёта временных характеристик информационных процессов следующая:
1. на основании описательной модели информационного процесса строится его графическая модель с использованием символов табл. П.1;
2. в построенной логической схеме выделяются типовые элементы (согласно
табл. П1.2 Приложения 1);
3. если типовые элементы в логической схеме отсутствуют, то необходимо её рекон-
фигурировать (в примере 2.2 показано, как это можно сделать; см. также [2.5] и
[2.6];
4. позиция 2 повторяется до тех пор, пока весь информационный процесс не будет
представлен одной операцией с рассчитанными искомыми характеристиками 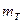
и 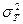 .
.
Таблица 2.2. Условные обозначения на логических схемах
| № п/п | Графическое изображение | Название элемента | Примечания |
| 1. | Операция | 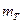 - среднее время выполнения операции; - среднее время выполнения операции; 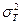 - дисперсия времени выполнения операции.
Допускается вместо - дисперсия времени выполнения операции.
Допускается вместо 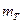 , , 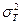 указывать функцию плотности распределения времени выполнения операции указывать функцию плотности распределения времени выполнения операции 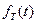 или, в случае детерминированной операции, её длительность Т или, в случае детерминированной операции, её длительность Т
| |
| 2. | Фиктивная операция | Операция, не требующая затрат времени на выполнение (допускается не изображать прямоугольник вообще) | |
| 3. | Разветвитель И | Все выходящие связи инициируются одновременно | |
 4.
4.
| Разветвитель ИЛИ (по условию) | Внутри ромба записывается условие ветвления. В схемах, подготовленных для расчетов, этот символ заменяется символом 5 | |
 5.
5.
| Разветвитель ИЛИ (по вероятности) |

| |
 6.
6.
| Объединитель И | Выходная связь инициируется после инициализации всех входных связей | |
 7.
7.
| Объединитель ИЛИ | Выходная связь инициируется любой входной |
|
|
В позиции 1 табл. 2.2 в прямоугольнике, обозначающем «операцию», указываются ее характеристики. Как правило, это средняя длительность (mТ) и дисперсия длительности  . При детерминированных операциях указывается ее длительность Т; при случайной длительности допускается вместо mТ и
. При детерминированных операциях указывается ее длительность Т; при случайной длительности допускается вместо mТ и 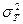 приводить плотность распределения вероятностей длительности операции.
приводить плотность распределения вероятностей длительности операции.
Отметим, что для получения mТ и 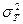 для некоторой операции требуется в свою очередь детально описать ее в терминах логических схем.
для некоторой операции требуется в свою очередь детально описать ее в терминах логических схем.
На основе символики табл. 2.2 могут быть введены типовые элементы логических схем информационных процессов (табл.2.3). Основное требование к перечню типовых элементов – это требование полноты: совокупность вводимых элементов должна быть достаточной для представления выбранного класса информационных процессов.
|
|
Таблица 2.3. Типовые элементы моделей процессов обработки данных
| № п/п | Графическое обозначение | Наименование | Примечания | ||
 1 1
| Последовательное соединение | ||||

| Параллельные операции | ||||

| Схема ветвления |
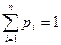
| |||

| Цикл | Если число повторений цикла фиксировано (например всегда равно N), то следует использовать типовой элемент 1 с N прямоугольниками | |||

| Цикл с ограниченным числом k повторений |
В таблице 2.4 приведены выражения для длительностей (Т), средних длительностей и дисперсий длительностей  выполнения действий, представленных в виде типовых элементов 1÷5 табл. 2.3 для случая, когда время выполнения каждой элементарной операции типовой схемы детерминированное (неслучайное).
выполнения действий, представленных в виде типовых элементов 1÷5 табл. 2.3 для случая, когда время выполнения каждой элементарной операции типовой схемы детерминированное (неслучайное).
В табл. 2.5 даны выражения для средней длительности (mТ) и  дисперсии дли-
дисперсии дли-
тельности выполнения действий, представленных типовыми схемами 1÷4 табл. 2.3 (типовой элемент 5 табл. 2.3 не рассматривался) в случае, когда длительность каждой элементарной операции типовой схемы – случайная. При этом всегда полагалось, что длительности различных операций типовой схемы – независимые случайные величины.
|
|