Согласно этой стратегии система восстанавливается после отказа. Если она проработала без отказов заданный интервал времени τ, то проводится профилактическая замена. Восстановления, которые производятся после отказов, называются аварийными. Как профилактические, так и аварийные восстановления являются полными.
Рис. Строго периодическое восстановление
Пусть ξτ и ητ — случайные времена соответственно между двумя последовательными аварийными восстановлениями и двумя последовательными восстановлениями произвольного типа. Тогда
где
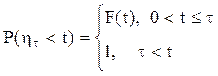
Если обозначить 
, то
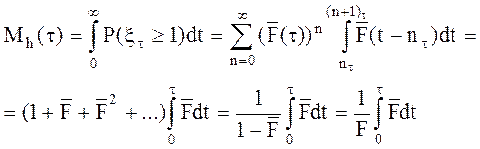
Таким образом
Моменты, в которые производятся аварийные восстановления, профилактические восстановления или восстановления произвольного типа, задают, согласно определению, процессы восстановления. Если обозначим через MP(τ) математическое ожидание времени между двумя профилактиками, то 
, 
и 
будут означать среднее число соответственно аварийных восстановлений, профилактик и восстановлений произвольного типа в единицу времени.
Очевидно
Отсюда следует:
где 
, 
Отсюда 
Оценка интенсивности ЭКСПЛУАТАЦИОННЫХ ЗАТРАТ.
Пусть ch и cp – средние затраты на аварийное и профилактическое восстановление соответственно, 0 < cp < ch < ¥. Если интервал восстановления равен τ, то интенсивность эксплуатационных затрат
или
Отсюда 
: 
Из условия оптимальности: 
, следует
После преобразований имеем
или
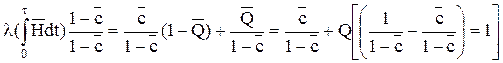
Отсюда
(4.39)
Оценка оптимальной интенсивности затрат
Отсюда
Таким образом
Пример: Пусть 
, 
. Соответствующая интенсивность отказов 
и 
, справедлива оценка 
. Из уравнения (4.39) получается уравнение для определения оптимального τ = τ*:
Действительно
где
Отсюда
Таким образом
Решение τ* этого квадратного уравнения (после подстановки 
) существует тогда и только тогда, когда 
:
В дальнейшем введем замену 
.
Тогда уравнение примет вид
или 
Введя замену U = 1 – x, получим 
Решая уравнение, найдем
Отсюда
или 
Разрешая уравнение относительно τ, найдем
Принимая 
получим 
Таким образом для оказывается, что 
. Это – интенсивность производственных затрат, которая получается при стратегии аварийных замен.
В дальнейшем предположим, что аварийное и профилактическое восстановления требуют.времени, равного соответственно dh и dp,(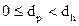
.) В этом случае первостепенный Очевидно интервалы времени Y, на которых система восстанавливается, определяются соотношением
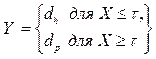
Отсюда следует
так что коэффициент готовности системы K(τ) задается в виде
Задача состоит в максимизации коэффициента готовности К(τ) надлежащим выбором интервала восстановления τ. Поскольку, однако, величины 
и R(τ) имеют одинаковый функциональный вид, оптимизационные задачи «минимизации R(τ)» и «максимизация К(τ)» эквивалентны. Вследствие этого оптимальное относительно К(τ) значение τ = τ* вновь является решением уравнения (4/39), если подставить в него 
.
Очевидно оптимальная периодичность будет удовлетворять условию оптимальности
В дальнейшем получим приближенное решение для случая, когда время безотказной работы подчиняется распределению Вейбулла. Для высоконадежных систем приближенно можно принять
С учетом введенных упрощений уравнение оптимальности примет вид
После преобразований получим
где 
Характер зависимости 
представлен на рис. 4.9.
Пример. Принимая 
, 
по графику получим 
. Таким образом периодичность обслуживания, при значении 
, будет равна
Рис. Зависимость параметра 
для различных 