ТЕХНИЧЕСКИХ СИСТЕМ
КОНСПЕКТ ЛЕКЦИЙ
| 1.1. Основные понятия теории надежности | |||||||||||||||||||||||||||
| Современная теория надежности охватывает широкий круг вопросов, а именно: разработка технических условий и требований, предъявляемых к техническим системам; построение этих систем; организация их эксплуатации, технического обслуживания и ремонта; замена изношенных и др. Проблемы, охватываемые теорией надежности, условно можно разделить на два взаимосвязанных направления: · физические основы надежности (связаны с изучением физико-химических свойств и параметров элементов изделий, происходящих в них физико-химических процессах, приводящих к отказам); · математическая теория надежности (основана на изучении статистических, вероятностных закономерностей отказов). Перспективное направление развития теории надежности определяется сочетанием математических методов с глубоким проникновением в физико-химическую сущность процессов, протекающих в изделии. Термины надежности стандартизованы. Согласно ГОСТу 27.002-85 надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортировки. Надежность – сложный показатель, который может включать в себя такие свойства, как: · безотказность (свойство непрерывно сохранять работоспособность до наступления предельного состояния в течение некоторой наработки); · долговечность (свойство сохранять работоспособность до наступления предельного состояния при установленной системе технического обслуживания и ремонта); · ремонтопригодность (свойство в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений и поддержанию и восстановлению работоспособности путем проведения ремонтов и технического обслуживания); · сохраняемость (свойство объекта непрерывно сохранять показатели безотказности, долговечности и ремонтопригодности в течение и после хранения и транспортировки). Для конкретных объектов и условий эксплуатации эти свойства могут иметь различную относительную значимость. Например, для сигнальных лампочек, предохранителей надежность определяется их безотказностью; для ремонтируемых объектов (таких как металлорежущие станки, бытовые стиральные машины, автомобили) важнейшими свойствами являются долговечность, ремонтопригодность. | |||||||||||||||||||||||||||
| 1.2. Показатели надежности | |||||||||||||||||||||||||||
Для решения практических вопросов необходимы показатели, характеризующие степень надежности оборудования с количественной стороны. Эти количественные характеристики и называются показателями надежности.
Показатели надежности рассматриваются при государственной аттестации качества продукции. Наличие их позволяет производить инженерные расчеты надежности, устанавливать обоснованные технические требования к надежности проектируемых изделий, делать сравнительную оценку изделий по их надежности и принимать основные решения при организации технического обслуживания и ремонта в системе ППР.
По ГОСТу 27.002.-83 и 23.642-79 все показатели надежности делят на два вида: единичные и комплексные. Единичные – количественно характеризуют только одно из свойств надежности: безотказность, долговечность, ремонтопригодность и т.д. Комплексные показатели одновременно характеризуют несколько свойств надежности, например, безотказность и ремонтопригодность объекта и т.д. Показатели надежности приведены в таблице 1.
Таблица 1- Основные показатели надежности
Вероятность безотказной работы P(t) – вероятность того, что в пределах заданной наработки отказ объекта не возникает. Средняя наработка до отказа Т1 – математическое ожидание наработки объекта до первого отказа. Интенсивность отказов l(t) – условная плотность вероятности возникновения отказа невосстанавливаемого объекта, определяемая для рассматриваемого момента времени при условии, что до этого момента отказ не возник. Параметр потока отказов w(t) – отношение среднего числа отказов восстанавливаемого объекта за произвольно малую его наработку к значению этой наработки. Наработка на отказ Т0 – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки. Установленная наработка до отказа tо.у. – наработка до установленных в технической документации видов отказов, которую должен иметь каждый объект при заданных условиях эксплуатации. Вероятность восстановления Р(tв) – вероятность того, что время восстановления работоспособности объекта не превысит заданного. Среднее время восстановления tв – математическое ожидание времени восстановления работоспособности (собственно ремонта). Внезапные отказы в период нормальной эксплуатации определяются случайными неблагоприятными сочетаниями большого количества факторов. Случайность связана с тем, что причины события для нас являются скрытыми. Поэтому надежность необходимо рассматривать в вероятностном аспекте. |
1.3. Аналитические зависимости изменения вероятности безотказной работы машины
Параметры надежности используются в статистической форме для оценки состояния объектов и в вероятностной – для прогнозирования. Первые выражаются в дискретных числах и при достаточно большом количестве испытаний принимаются за истинные характеристики надежности.
Рассмотрим результаты проведенных для оценки надежности испытаний значительного числа N0 элементов в течение времени t. К концу испытаний остается Nи (исправных) и Nот (отказавших) элементов, тогда:
1. Вероятность отказов
Если испытания проводятся с целью прогнозирования надежности, то q(t) можно рассматривать как вероятность отказов (при достаточно большом N0). |
Вероятность безотказной работы
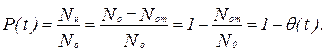
| (2) |
Так как безотказная работа и отказ – взаимно противоположные состояния изделия, их сумма равна единице:
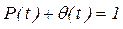 . .
| (3) |
При анализе зависимостей (1) и (2) следует, что при t=0, Nот=1,  , следовательно,
, следовательно, 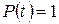 ; при t ®¥ Nот= N0,
; при t ®¥ Nот= N0, 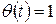 , Р(t) =0.
, Р(t) =0.
Следовательно, вероятность безотказной работы за рассматриваемый промежуток времени изменяется в указанных пределах. Покажем, что кривой, соответствующей этому изменению, является экспонента.
3. Плотность вероятности отказов f(t), или вероятность отказов в единицу времени, есть производная от функции вероятности отказов по времени или наработке в других единицах:
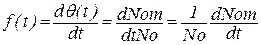 , ,
| (4) | |
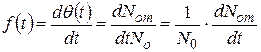 . .
| (5) |
Выразим вероятность отказов и вероятность безотказной работы через плотность вероятности отказов. По определению
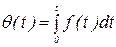
|
вероятность отказов за определенный промежуток времени равна сумме плотностей вероятностей отказов в промежутке времени и при t®¥:

| 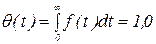 , ,
|
что следует из предыдущих рассуждений. Из выражения (3)
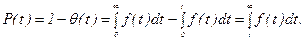
| (6) |
4. Интенсивность отказов l(t)– это вероятность отказа в единицу времени при условии, что отказ до этого времени не наступал, то есть это скорость изменения отказа в единицу времени, отнесенная к числу исправных элементов (постоянных в указанном промежутке времени):
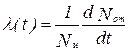 . .
| (7) |
Из выражений (4) и (7) следует, что f(t) и l(t) отличаются знаменателями. Первое определяется относительно N0, а второе – N и.
Из выражений (4) и (5) следует
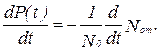
|
Умножив числитель и знаменатель на N и, получим
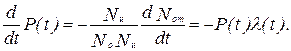
| (8) |
Преобразуя выражение (8), получим:
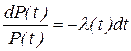 . .
|
Проинтегрируем:
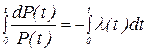 , ,
|
получим
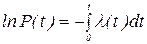 , ,
|
или
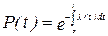 . .
| (9) |
При нормальной эксплуатации объектов интенсивность отказов l(t)=const.= l, тогда
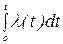
принимает выражение lt, а зависимость (9) представляется как
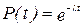 . .
| (10) |
Из этого следует, что вероятность безотказной работы изменяется по экспоненте (рис. 1).
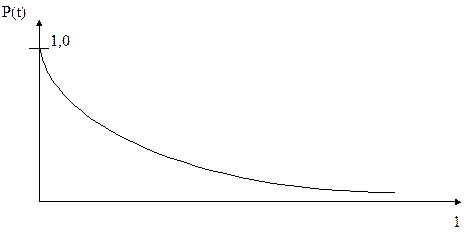
Рис. 1. Характер изменения безотказной работы Р(t) объекта
в зависимости от пробега (l)
В математической статистике закон распределения случайной величины Х может быть задан в аналитическом виде или таблицей, где против каждого возможного Х=хi стоит соответствующая вероятность pi.

 = 1,0 ч
= 1,0 ч
 .
.



 . (12)
. (12)
 Pc(t)=[1-θ1(t)][1-θ2(t)]…[1 θn(t)]≈1[θ1(t)+θ2(t)+…θn(t)]
Pc(t)=[1-θ1(t)][1-θ2(t)]…[1 θn(t)]≈1[θ1(t)+θ2(t)+…θn(t)]
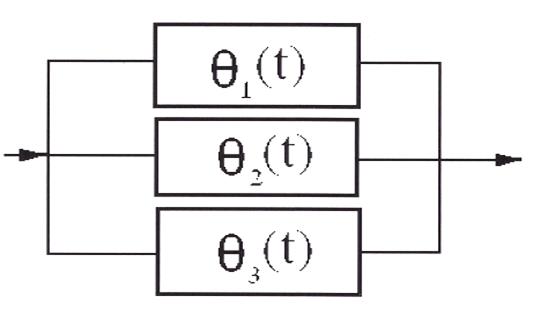

 (t)=θ3(t)=…θn(t),θc(t)=θ1n(t)
и тогда
(t)=θ3(t)=…θn(t),θc(t)=θ1n(t)
и тогда

 .
.
 K = R\ Δx
K = R\ Δx
 х.
х.







 P(t)=θ′(t)
P(t)=θ′(t)

 , т.е. при длительной эксплуатации ремонтируемого изделия поток отказов становится стационарным. Наработка на отказ Т0 является наглядной характеристикой надежности, поэтому широко используется на практике.
, т.е. при длительной эксплуатации ремонтируемого изделия поток отказов становится стационарным. Наработка на отказ Т0 является наглядной характеристикой надежности, поэтому широко используется на практике.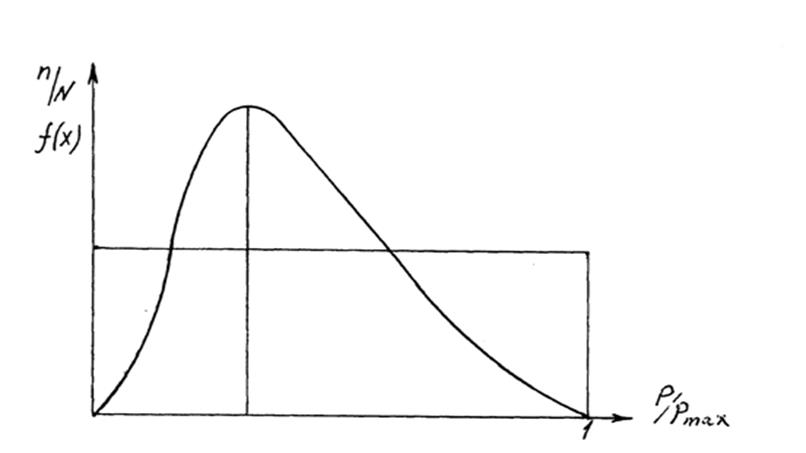 Рис. 6. Кривая относительного изменения нагрузки
Для вновь создаваемых машин эту функцию можно рассматривать как плотность вероятности (плотность распределения) f(x);
· затем строят функцию распределения F(x) (рис. 7), причем функции F(x) и f(x) связаны известным соотношением f(x)=F’(x). Функция f(x) показывает вероятность работы с каждым значением нагрузки, а площадь, очерчиваемая кривой функции распределения, равна единице.
Рис. 6. Кривая относительного изменения нагрузки
Для вновь создаваемых машин эту функцию можно рассматривать как плотность вероятности (плотность распределения) f(x);
· затем строят функцию распределения F(x) (рис. 7), причем функции F(x) и f(x) связаны известным соотношением f(x)=F’(x). Функция f(x) показывает вероятность работы с каждым значением нагрузки, а площадь, очерчиваемая кривой функции распределения, равна единице.
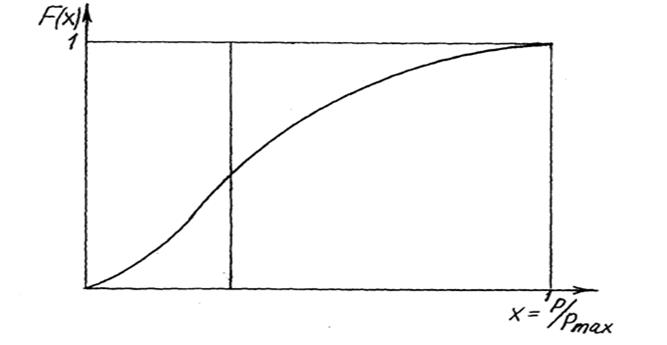 Рис. 7. Функция распределения
Распределение нагрузок для разных машин сводят к четырем известным типовым, хорошо изученным в математике кривым (рис. 8), которые определяют следующие режимы работы: СР – средний равновероятностный, T (или b-распределение – тяжелый), С(н) – средний нормальный (Гауссово распределение), Л (или g-распределение) – легкий.
Функция вероятности распределения нагрузок для каждого из них известна. Так, для кривой С(н) она равна:
F(x) = (1/s√2π)•∫℮-(x-x¯)2/2S2dx,
Рис. 7. Функция распределения
Распределение нагрузок для разных машин сводят к четырем известным типовым, хорошо изученным в математике кривым (рис. 8), которые определяют следующие режимы работы: СР – средний равновероятностный, T (или b-распределение – тяжелый), С(н) – средний нормальный (Гауссово распределение), Л (или g-распределение) – легкий.
Функция вероятности распределения нагрузок для каждого из них известна. Так, для кривой С(н) она равна:
F(x) = (1/s√2π)•∫℮-(x-x¯)2/2S2dx,  где x = 0,5 Xmax, s = 0,2 Xmax.
Многочисленные исследования нагрузок, возникающих при эксплуатации машин, позволяют сделать следующий вывод: режим работы С(н) характерен для большинства универсального оборудования; режим СР – для более интенсивно эксплуатируемого специализированного оборудования; режим Т – для горного оборудования.
где x = 0,5 Xmax, s = 0,2 Xmax.
Многочисленные исследования нагрузок, возникающих при эксплуатации машин, позволяют сделать следующий вывод: режим работы С(н) характерен для большинства универсального оборудования; режим СР – для более интенсивно эксплуатируемого специализированного оборудования; режим Т – для горного оборудования.
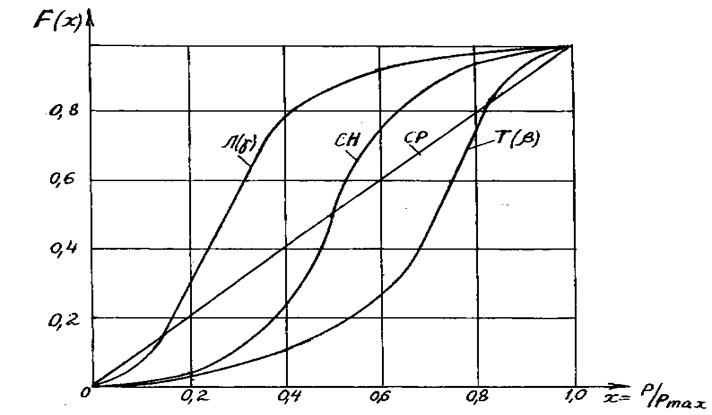 Рис. 8. Типовые (расчетные) режимы работы машин
Динамические нагрузки всегда возникают при работе машины. Большинство машин работает в условиях прерывистого рабочего процесса, и динамические нагрузки неизбежно связаны с разгоном, торможением и реверсированием. Все механизмы возвратно-поступательного и периодического движения (кривошипно-ползунные, кулисные) работают в динамическом режиме нагрузок. Большинство динамических нагрузок возникает из-за недостаточной уравновешенности быстровращающихся деталей. Так, смещение на 0,1 мм центра тяжести от оси вращения ротора, вращающегося со скоростью n=3000 об/мин, приводит к возникновению центробежной вращающейся силы, равной силе тяжести ротора, действие которой многократно опаснее действия самой силы тяжести. При вращении вала на подшипниках скольжения возникает нестабильная работа (вал “плавает”, возможны вибрации), а при установке валов на подшипниках качения без натяга возникает проскальзывание тел качения, повышается износ. Некоторые машины, работающие в зарезонансной области, при разгоне и остановке проходят резонансные зоны. При зависимости момента на валу привода от частоты вращения может возникнуть возрастание моментов при прохождении через зоны резонансов, что необходимо учитывать при расчете деталей на усталость. В прямозубых передачах вход в зацепление вызывает ударные нагрузки, определяемые упругостью зуба (упругая деформация и погрешность основного шага). Кроме того, знакопеременность силы трения при прохождении зуба через полюс зацепления вызывает динамические нагрузки. Динамическая неустойчивость ременных передач объясняется биением шкивов, неоднородностью ремня, крутильными колебаниями шкивов при малых скоростях ремней. В валах с подшипниками качения переменная жесткость подшипников по углу поворота может вызвать вибрации. При расчетах колебаний приводов машин необходимо учитывать упругость и демпфирование электромагнитной связи между статором и ротором приводного двигателя, так как электродвигатели представляют собой мощные демпферы.
Рис. 8. Типовые (расчетные) режимы работы машин
Динамические нагрузки всегда возникают при работе машины. Большинство машин работает в условиях прерывистого рабочего процесса, и динамические нагрузки неизбежно связаны с разгоном, торможением и реверсированием. Все механизмы возвратно-поступательного и периодического движения (кривошипно-ползунные, кулисные) работают в динамическом режиме нагрузок. Большинство динамических нагрузок возникает из-за недостаточной уравновешенности быстровращающихся деталей. Так, смещение на 0,1 мм центра тяжести от оси вращения ротора, вращающегося со скоростью n=3000 об/мин, приводит к возникновению центробежной вращающейся силы, равной силе тяжести ротора, действие которой многократно опаснее действия самой силы тяжести. При вращении вала на подшипниках скольжения возникает нестабильная работа (вал “плавает”, возможны вибрации), а при установке валов на подшипниках качения без натяга возникает проскальзывание тел качения, повышается износ. Некоторые машины, работающие в зарезонансной области, при разгоне и остановке проходят резонансные зоны. При зависимости момента на валу привода от частоты вращения может возникнуть возрастание моментов при прохождении через зоны резонансов, что необходимо учитывать при расчете деталей на усталость. В прямозубых передачах вход в зацепление вызывает ударные нагрузки, определяемые упругостью зуба (упругая деформация и погрешность основного шага). Кроме того, знакопеременность силы трения при прохождении зуба через полюс зацепления вызывает динамические нагрузки. Динамическая неустойчивость ременных передач объясняется биением шкивов, неоднородностью ремня, крутильными колебаниями шкивов при малых скоростях ремней. В валах с подшипниками качения переменная жесткость подшипников по углу поворота может вызвать вибрации. При расчетах колебаний приводов машин необходимо учитывать упругость и демпфирование электромагнитной связи между статором и ротором приводного двигателя, так как электродвигатели представляют собой мощные демпферы.
 Рис. 9. Схема механизма сцепления автомобиля
При переключении скорости выжимается сцепление и рычаги 10 через подшипник 7, систему рычагов 6 отводят нажимной диск 3 и диски сцепления 2, отключая движение от двигателя. Передача переключается. Затем плавно отпускается педа
Рис. 9. Схема механизма сцепления автомобиля
При переключении скорости выжимается сцепление и рычаги 10 через подшипник 7, систему рычагов 6 отводят нажимной диск 3 и диски сцепления 2, отключая движение от двигателя. Передача переключается. Затем плавно отпускается педа