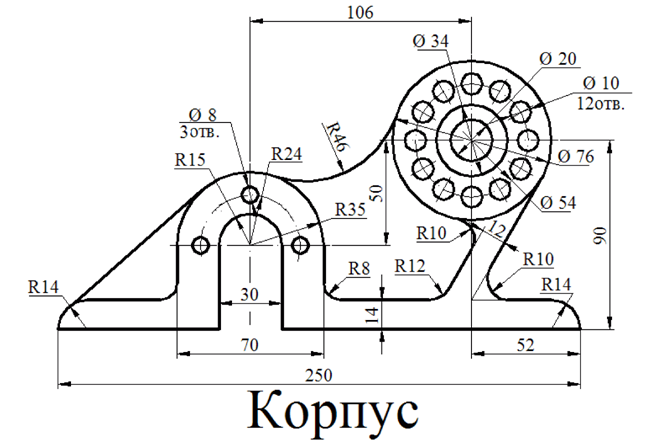
Сопряжения
В очертаниях технических форм часто встречаются плавные переходы от одной линии к другой. Контуры этих изделий вычерчиваются с использованием сопряжений. Сопряжением называют плавный переход от одной линии к другой ( выполненный с помощью дуги окружности, которую называют дугой сопряжения). Места перехода называются точками сопряжения.
При построении сопряжений необходимо знать:
R -радиус дуги сопряжения. Этот радиус задают численным значением или отрезком.
О - Найти центр сопряжения;
К - Определить точки сопряжения. Точкой сопряжения называют переход одной линии в другую
Построение сопряжений основано на следующих положениях геометрии.
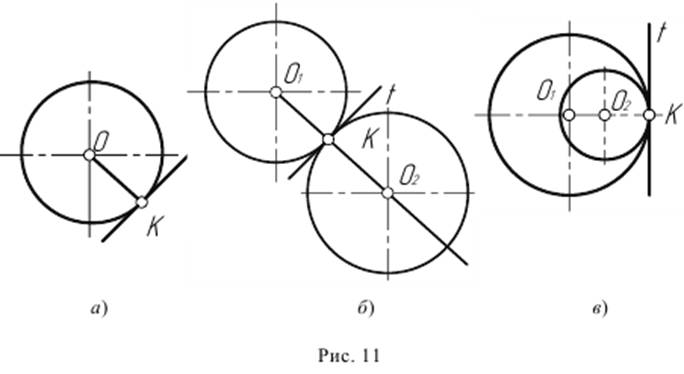
1. Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
2. Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Из всего многообразия сопряжений различных линий выделяют основные виды сопряжений:
Сопряжение двух различно расположенных прямых линий с помощью дуги окружности.
Как известно, две прямые могутпересекаться под прямым, острым и тупым углом.
На рис.1.27 показаны примеры сопряжения радиусом R двух прямых,расположенных под прямым (рис.1.27, а), острым (рис.1.27, б) и тупым углом (рис.1.27, в). Рассмотрим методику построения сопряжения двух прямых.Вначале определяем центр сопряжения. Проводим параллельно каждойиз этих прямых на расстоянии R вспомогательные прямые. Полученная припересечении этих прямых точка О и будет центром сопряжения.Затем из этой точки опускаем перпендикуляры на данные прямые. Точкипересечения этих перпендикуляров с прямыми – точки N и N1 являютсяточками сопряжения. Из полученного центра сопряжения точкиО, с помощьюциркуля проводим дугу радиусом R, которая проходит через точкисопряжения N и N1. Таким образом, полученная дуга является сопряжением двух прямых.
|
|
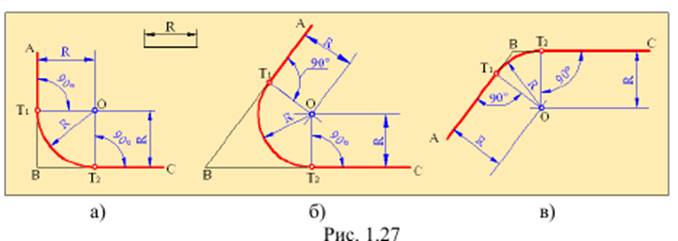
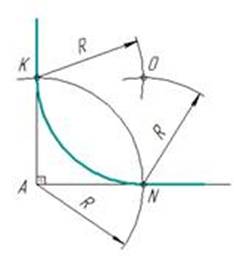
Примечание.Для прямых углов центр сопряжения удобнее находить с помощью циркуля
Сопряжение прямой и окружности.
Сопряжение прямой с окружностью может быть внешним или внутренним.
Рассмотрим построение внешнего сопряжения прямой с окружностью.
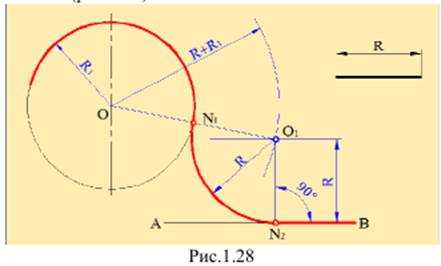
Рассмотрим 1пример (внешнего сопряжения) построения сопряжения окружности радиусом R1 с центром в точке О с прямой АВ. Радиус сопряжения R (рис.1.28) Для этого из центра точки О проведём вспомогательную дугу радиусом R+R1. Далее, на расстоянии R от прямой АВ проводим дополнительную параллельную ей прямую и находим точку пересечения этой прямой с дугой – точку О1. Эта точка будет центром сопряжения. После этого находим точки сопряжения. Соединяем точки О и О1 и определяем первую точку сопряжения N1. Из точки О1 опускаем перпендикуляр на прямую АВ и находим вторую точку сопряжения - точку N2. И, наконец, строим дугу сопряжения радиусом R, с центром в точке О1 и проходящую через точки N1 и N2.
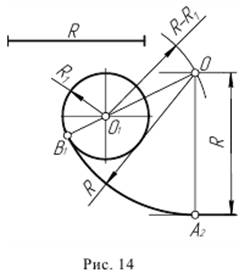
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центраО1, радиусом R - R1.
|
|
3. Сопряжение двух окружностей -может быть внешним, внутренним и смешанным.
Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряженияследует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами R1 и R2 дугой заданного радиуса R (рис. 15а).
1. Для нахождения центра сопряжения О проведем окружность m1, удаленную от данной окружности m на расстояние R. Так как сопряжение с внешним касанием, то радиус окружности m1 равен R1 + R.
2. Радиусом R2 + R проведем окружность n1, удаленную от данной окружности n на расстояние R.
3. Найдем центр сопряжения О как точку пересечения окружностей m1 и n1.
4. Найдем точку сопряжения А как пересечение линии центров O1 O с дугой m.
5. Аналогично найдем точку В как пересечение линии центров О2 О с дугой n.
6. Проведем дугу сопряжения АВ.
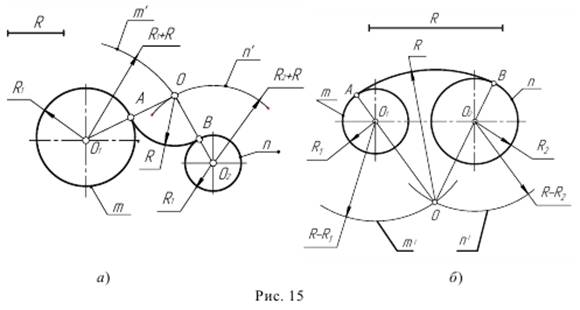
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами R1 и R2 дугой радиусом R (рис. 15б).
1. Для нахождения центра сопряжения О проведем окружность m1 на расстоянии R- R1 от данной окружности m.
2. Проведем окружность n1 на расстоянии R – R2 от данной окружности n.
3. Центр сопряжения О найдем как точку пересечения окружностей m1 и n 1.
4. Точку сопряжения А найдем как точку пересечения линии центров О О1 сзаданной окружностью m.
5. Точку сопряжения В найдем как точку пересечения линии центров O O2 c заданной окружностью n.
6. Проведем дугу сопряжения AВ с центром в точке O.
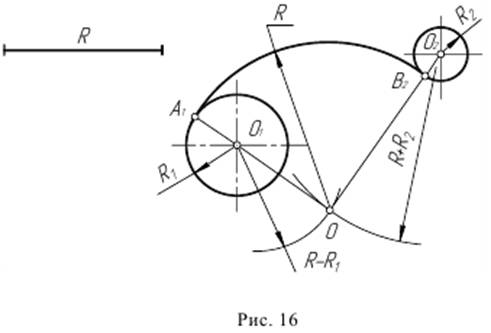
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне-внутренним касанием. Принцип построения сопряжений двух окружностей, когда задана некоторая точка на одной из окружностей, аналогичен рассмотренным выше примерам.
|
|
Практическая работа:
- в тетради на формате А4 (лист расположить по горизонтали), начертить внутреннюю рамку чертежа;
- провести осевые и центровые линии, взяв расстояние между ними согласно размерам детали и учитывая равномерность распределения изображений на поле чертежа;
- провести дуги окружностей, окружности и прямые линии, положение которых определено заданными размерами и не требует дополнительных построений;
- выполнить геометрические построения и сопряжения. Предварительные построения выполнять тонкими линиями твердым карандашом (Т или 2Т);
- нанести выносные и размерные линии, надписать размерные числа
(шрифт 5);
- проверить правильность выполнения чертежа и обвести чертеж карандашом (ТМ или М). Вначале обвести дугу окружностей и окружности, затем – прямые линии. Обвести внутреннюю рамку чертежа. Все построения сопряжений сохранить;