Построим формальную логическую систему на основе имеющейся алгебраической системы.
Предметные константы:
Константы 1 и 0 – соответствуют картежам, описанным выше.
Множество переменных:
{A1, A2,…,А81 } – множество картежей, обозначенных латинскими буквами. Вид картежа описан ранее.
Предикатные символы:
Предикат W’ (A, B) соответствует отношению меньше по количеству выпуклостей алгебраической системы; выполняется, если А <’ В.
Предикат W” (A, B) соответствует отношению меньше по количеству вогнутостей алгебраической системы; выполняется, если А <” В.
Предикат S’ (A, B) соответствует отношению больше по количеству выпуклостей алгебраической системы; выполняется, если А >’ В.
Предикат S” (A, B) соответствует отношению больше по количеству вогнутостей алгебраической системы; выполняется, если А >” В.
Предикат R’ (A, B) соответствует отношению равенства по количеству выпуклостей алгебраической системы; выполняется, если А =’ В.
Предикат R” (A, B) соответствует отношению равенства по количеству вогнутостей алгебраической системы; выполняется, если А =” В.
Предикат R (A, B) соответствует отношению равенства алгебраической системы; выполняется, если А = В.
Функциональные символы:
f+ соответствует операции наложения.
f2+ (A, B) ó A + B.
F* соответствует операции склеивания.
f2* (Ai, Bj) ó Ai * Bj, i,j=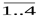 
, |i – j| = 2.
f-1 соответствует операции инверсия.
f-1 (A) ó (A)-1.
Синтаксис термов:
Терм - всякая предметная константа, предметная переменная либо функциональная форма.
Предикатная форма – предикатная константа, соединяющаяся с подходящим числом терм:
P(t1,.., tm);
P().
Если fn – функциональный символ, t1, t2, …, tn – термы, то fn (t1, t2, …, tn) также терм.
Понятие формулы в логике определим следующим образом:
всякая предикатная форма есть формула;
если А – формула, то А-1 тоже формула;
если А и В - формулы, то А + В, А * В также формулы;
если А - формула и хА - переменная, то "xА и $xA - формулы;
других формул нет.
Для данной формальной логической системы справедливы следующие аксиомы:
E (f+(A, 0), A),
E (f+(A, A), A),
"(i | i=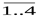 
) E (f*(Ai, f-1(Ai)),1i),
E (f+(A, B), f+(B, A)),
"(A | f-1(Ai) = 1i, i= 
) E (f*(Ai, 1i),Ai)
Формула общезначима (является тавтологией), если она истинна в любой интерпретации.
Формула невыполнима (противоречива, тождественно ложна), если она при всех интерпретациях является ложной.
Множество теорем определим как множество общезначимых формул.
Приведем примеры логического вывода:
1)Пусть А, В, С- любые формулы, тогда выводами являются следующие последовательности:
а)A É (B É A);
б)A É (B É A), A É (B É A);
в)A É (A É A), (A É (B É C)) É ((A É B) É (A É C))
г)(ØA ÉØB) É (B É A), B É (A É B),ØA É (ØB É ØA);
д)(A É (A É A)) É ((A É A) É (A É A)), (A É (A É A)),(A É A) É (A É A):
.
2)Выведем: ╞ A(u) É $uA(u), где A(u) – любая предикатная формула.
Формула"uØA(u) É ØA(u), согласно аксиоме "xF(x) É F(y), выводима. Формула (p É Øq) É (q É Øp) – тавтология и следовательно выводима. Из этого следует, что предикатная формула (A É ØB) É (B É ØA), где А, В- любые формулы, выводима в исчислении предикатов. Тогда выводима и формула 
. Отсюда по правилу заключения ╞A(u)ÉØ"uØA(u), то есть ╞A(u) É $uA(u).
Также можно использовать и следующие правила вывода:
╞ A É B, ╞ B É C, то ╞ A É C
A╞ B, C ╞ D, B, D ╞ E, то A, B ╞ E
╞ A É (B É C), то╞ B É (A É C)
╞ AÉ (B É C), то A + B É C
╞ A + B É C, то╞ A É (B É C)
╞ - символ «выводимости »