Лекция 2. Базис. Скалярное произведение.
Базис, Разложение вектора по базису. Координаты вектора. Линейные операции над векторами, заданными своими координатами. Ортонормированный базис i, j, k. Скалярное произведение векторов, его механический смысл. Формула для скалярного произведения векторов, заданных своими координатами в базисе i, j, k. Вычисление длины вектора, косинуса угла между векторами и проекции вектора на направление. Равенство координат вектора в ортонормированном базисе проекциям этого вектора на направления соответствующих базисных векторов. Направляющие углы вектора, свойство их косинусов.
П. 1. Базис. Разложение вектора по базису.
Определение. Базисом системы векторов называется такая подсистема этой системы, которая обладает двумя свойствами:
1) Подсистема - линейно независимая система векторов.
2) Каждый вектор системы является линейной комбинацией векторов этой подсистемы.
Пример 1. Найти базис системы векторов  .
.
Решение. Существуют разные практические способы для определения базиса. Найдем базис этой системы по определению базиса.
Пусть  - базис. Проверим свойства базиса.
- базис. Проверим свойства базиса.
1) 
 т.е.
т.е.  - линейно независимы.
- линейно независимы.
2) 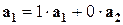

Значит  - базис системы векторов
- базис системы векторов  .
.
Аналогично  - базис,
- базис,  - базис.
- базис.
Замечание. Из определения базиса следует:
1) Система векторов может иметь несколько базисов.
Если  - линейно независимая система векторов, то базисом является сама эта система.
- линейно независимая система векторов, то базисом является сама эта система.
2) Базисом на плоскости является упорядоченная пара ненулевых неколлинеарных векторов этой плоскости.
3) Базисом в пространстве является упорядоченная тройка ненулевых некомпланарных векторов этого пространства.
Теорема 1. Конечная система векторов, обладающая хотя бы одним ненулевым вектором, имеет базис. Любые два базиса данной системы векторов состоят из одинакового числа векторов.
Определение. Базис называется ортогональным, если он состоит из векторов, лежащих на взаимно перпендикулярных прямых. Базис называется ортонормированным, если он ортогональный и состоит из единичных векторов.
Ранг конечной системы векторов.
Определение. Рангом конечной системы ненулевых векторов называется число векторов в каком-нибудь базисе этой системы. Ранг нулевой системы векторов по определению число 0. Обозначается  .
.
Замечание. Из теоремы 1 следует, что любой базис данной системы состоит из одинакового числа векторов, значит понятие ранга определено корректно.
Пример 3. Дана система векторов  . Базис этой системы найден в примере 2, значит
. Базис этой системы найден в примере 2, значит  .
.
Определение. Две системы векторов:
 (1)
(1)
 (2)
(2)
называются эквивалентными, если каждый вектор системы (1) является
линейной комбинацией векторов системы (2) и наоборот. Обозначение  .
.
Пример. Рассмотрим две системы векторов:
 (3)
(3)
 (4)
(4)
Каждый вектор из системы (3) представим в виде:
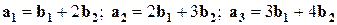
Из системы (4):

Значит по определению системы (3) и (4) эквивалентны.
■
Теорема 2. Если системы векторов (1) и (2) линейно независимы и эквивалентны, то они состоят из одинакового числа векторов.
■
Элементарные преобразования системы векторов.
Элементарными преобразованиями системы векторов называются преобразования вида:
1) Умножение какого-либо вектора системы на скаляр  .
.
2) Прибавление к одному из векторов системы любого другого, умноженного на скаляр.
3) Исключение из системы и добавление в систему  - вектора.
- вектора.
4) Перестановка местами любых двух векторов системы.
Теорема 3. Если однасистема векторов получена из другой системы векторов в результате цепочки элементарных преобразований, то эти системы эквивалентны.
Пример. Найти все базисы следующих систем векторов, используя элементарные преобразования системы векторов.
1)  2)
2) 
Решение:
1) Вычислим ранг системы векторов.

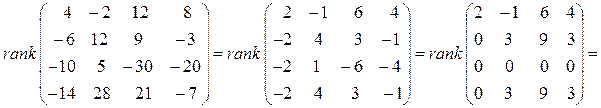
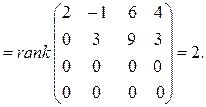
В базисе содержится два вектора. Базисом могут являться следующие системы:  .
.
Вычислим  .
.


Значит, 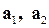 – базис.
– базис.
Вычислим  .
.


Следовательно,  не является базисом.
не является базисом.
Вычислим  .
.


Значит,  – базис.
– базис.
Вычислим  .
.
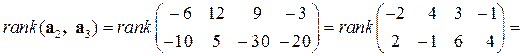
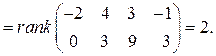
Значит,  – базис.
– базис.
Вычислим  .
.


Следовательно,  не является базисом.
не является базисом.
Вычислим 


Значит, 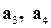 – базис.
– базис.
Таким образом,  – все базисы данной системы векторов.
– все базисы данной системы векторов.
Теорема 4. Любой геометрический вектор  пространства можно разложить по векторам базиса
пространства можно разложить по векторам базиса 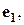

 и это разложение единственно:
и это разложение единственно:
 =
= 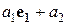

 (5)
(5)
Определение. Скалярные величины 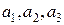 в разложении вектора
в разложении вектора  по векторам базиса
по векторам базиса 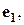

 в формуле (5) называются координатами вектора
в формуле (5) называются координатами вектора  в базисе
в базисе 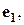

 .
.
Записывается  = (
= (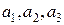 ).
).
Замечание. Упорядоченные векторы – это векторы, взятые в указанном порядке.
Определение. Упорядоченная тройка некомпланарных векторов a,b,c
называется правой, если при приведении этих векторов к общему началу, кратчайший поворот от a к b виден из конца вектора c против часовой стрелки. Если кратчайший поворот от a к b совершается почасовой стрелке, то тройка векторов a,b,c – левая.

Правая тройка. Левая тройка.
Определение. Упорядоченная тройка взаимно перпендикулярных единичных векторов i, j, k называется ортонормированным базисом в трёхмерном пространстве.
В дальнейшем за ортонормированный базис принимаем правую тройку векторов i, j, k. Произвольный вектор пространства  можно разложить по векторам ортонормированного базиса i, j, k:
можно разложить по векторам ортонормированного базиса i, j, k:
 =
=  i +
i +  j +
j + 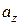 k, или
k, или  =(
=( ,
,  ,
, 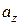 ). (6)
). (6)
Аналогично на плоскости:  =
=  i +
i +  j, или
j, или  =(
=( ,
,  ), (7)
), (7)
на оси:  =
=  i или
i или  =(
=( ). (8)
). (8)
Формулы (6), (7), (8) называются разложением вектора по ортам координатных осей.
Замечание. Проекции вектора  на базисные орты i, j, k совпадают с координатами вектора
на базисные орты i, j, k совпадают с координатами вектора  в базисе i, j, k. То есть, если
в базисе i, j, k. То есть, если  =
=  i +
i +  j +
j + 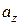 k,
k,
то  =
= 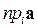 ,
,  =
=  ,
, 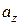 =
= 