Эта формула известна из школы.
Замечание. Вывод этой формулы при помощи векторной алгебры – см. лекцию №4, стр.33. (Крищенко А.П…..)
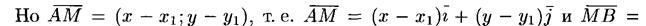
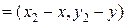, то есть 
Тогда, векторное уравнение можно записать в координатной форме:
Полученные формулы называются формулами деления отрезка в данном отношении. В частности, при 
, то есть, если АМ=МВ, то формулы
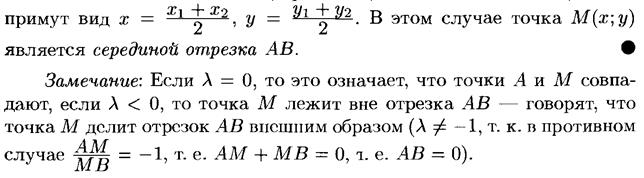
4.3. Вычисление площадей и объемов
(см. стр. 34-35 электронной лекц. №4 Крищенко А.П.)
Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.
Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.
Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3;-1;2). Найти его площадь.
Решение.
Для определения площади треугольника ABC найдем координаты векторов 
и 
: 
= (1 - 4; 2 - 4; 3 – 4) = (-3; -2; -1), = (3 - 4; -1 - 4;2 – 4) = (-1; -5; -2). Затем вычислим их векторное произведение:
х = 
Модуль этого векторного произведения равен
. Следовательно, 
. 
Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах 
. Таким образом, объем этой пирамиды равен VSABC = 
Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; -1; 1), B(5; 5; 4), C(3;2;-1), S(4; 1; 3).
Вычисляем координаты векторов, направленных по ребрам пирамиды: - = (5 - 2; 5 - (-1); 4 – 1) = (3;6;3), = (3 - 2; 2 - (-1);-1 – 1) = (1;3; -2), 
= (4 - 2; 1 - (-1); 3 – 1) = (2;2;2), и определяем объем с помощью смешанного произведения найденных векторов:
, 
Линии на плоскости
Одну и ту же линию на плоскости можно задать разными способами: 1) уравнением в прямоугольных координатах;
2) уравнением в полярных координатах;
3) параметрическими уравнениями;
4) векторным уравнением.
Векторное уравнение линии.
В аналитической геометрии на плоскости возникают две основные задачи. Первая: зная геометрические свойства кривой, найти её уравнение.
Вторая: зная уравнение кривой, изучить её форму и свойства.
Примеры некоторых кривых.
1) Окружность.
Циклоида.
3) 
Построение линий с помощью сервиса 
.
Кривые, заданные в полярной системе координат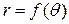 
:
.
Кривые, заданные в полярной системе координат ,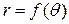 
:
.
Кривые, заданные параметрически 
:
.
Кривые, заданные параметрически , 
:
.
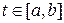Область, заданную неравенствами вида 
:
.
Пример. Построить график кривой в полярной системе координат:
.
Составляем запрос на построение графика кривой
Сервис 
строит кривую на отрезке 
:
Сервис 
строит кривую на отрезке 
:
■