Матрицы, виды матриц. Операции над матрицами и их свойства
П.1. Матрицы, виды матриц.
Пусть Р =(Р, +, ·, -, 0, 1)-поле скаляров. Рассмотрим матрицу А над полем Р.
, i =1… n; j =1…. n;
элемент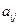 
расположен в i -ой строке, j -ом столбце.
Матрица имеет размер 
, т.е. в ней m строк и n столбцов.
Если 
, то матрица А квадратная матрица порядка n.
Обозначим 
- множество всех 
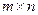матриц над полем Р.
Для матрицы А можно применить другое обозначение
Пример.
1. 
- матрица размерности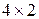 
.
2. 
- матрица размерности 
, (вектор-строка).
3. 
- матрица размерности 
, (вектор-столбец).
Другими словами:. Матрица А называется диагональной, если все её элементы, расположенные вне главной диагонали, равны нулю.
Квадратная матрица Е порядка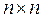 
, вида:
называется единичной матрицей, 
Пример. Если n=1, то E=(1)
Если n=2, то E= 
Если n=3, то E= 
В единичной матрице на главной диагонали расположены 1, а на остальных местах 0.
Пусть матрица 
т.е. 
Теорема 1. Если 
, то для любой 
, имеем ЕА = АЕ = А
Доказательство. АЕ = 
= 
= А.
Аналогично доказывается, что ЕА = А. ■
Равенство (1) показывает, почему матрица Е является единичной - она выполняет роль единицы при умножении матриц.
Определение. Матрица А называется нулевой матрицей, если все её элементы равны нулю.
Нулевая матрица обозначается 0 или 
.
Определение. Матрица, у которой строками являются соответствующие столбцы матрицы 
, называется транспонированной матрицы . Обозначается 
или 
.
То есть, строками транспонированной матрицы являются столбцы матрицы , а столбцами – строки .
Пример. 
.
.
Замечание. П.2. С.7-9 только из этой лекц. Затем п.2 – п.7 лучше исп. Эл. Лекцию Кр. №10, с. 97-103. Затем упр.:С.10-16 этой лекц.
Замечание. П.2. С.7-9 только из этой лекц. Затем п.2 – п.7 лучше исп. Эл. Лекцию Кр. №10, с. 97-103. Затем упр.:С.10-16 этой лекц.
|
|
П.2. Линейные операции над матрицами.
(См. электронную лекцию №10, с. 95-97)
Определение. Пусть А и В - две 
матрицы над полем Р.
, 
. 
То есть матрицы называются равными, если на одинаковых местах стоят одинаковые элементы и размер матриц одинаков.
Определение. Пусть А и В - две матрицы над полем Р. Суммой матриц А и В называется матрица, у которой в i -ой строке и j -ом столбце расположен элемент 
, т.е. 
.
Другими словами: чтобы сложить 2 матрицы, надо сложить их соответствующие элементы.
Пример.
Определение. Пусть 
и 
Произведением скаляра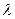 
на матрицу А называется матрица, у которой в i -ой строке и j -ом столбце расположен элемент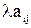 
, т.е. 
.
Другими словами: чтобы скаляр 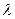умножить на матрицу А, нужно все элементы матрицы А умножить на скаляр .
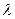Определение. Противоположной к матрице А называется матрица: 
Свойства сложения и умножения матриц на скаляры.
1. 
абелева группа.
Доказательство.
а) Из определения следует выполнение аксиом абелевой группы.
б) 
.
в) 
.
г) 
; 
. ■
2. 
Р, 
: 
3. 
Р, 
: 
4. 
Умножение матриц
Пусть 
, 
,
Определение. Произведением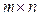 
матрицы А на 
матрицу В называется 
матрица 
, где
,
Пишем 
.
Говорят, что 
- скалярное произведение i -ой строки матрицы А на j -ый столбец матрицы В.
Пример.
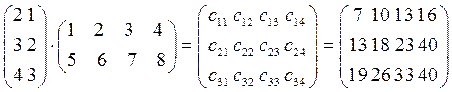
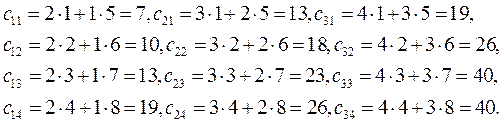
Свойства умножения матриц.
1. Умножение матриц ассоциативно, т.е. 
матриц А, В, С имеем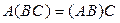 
, если определено произведение матриц АВ и ВС.
Доказательство. Пусть 
. Так как определено произведение АВ, и 
, и определено произведение ВС, то 
.
|
|
Определим матрицы 
и 
:
матрица.
матрица.
Матрицы и имеют одинаковый размер.
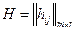
- это произведение матриц А и ВС 
Из равенства (2) имеем:
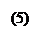
Подставим (5) в (4):
То есть 
Из равенства (3) имеем:
Подставим (7) в (6). Тогда
Матрицы и 
имеют одинаковый размер и на одинаковых местах стоят одинаковые элементы 
; значит 
= . ■
2. Умножение матриц дистрибутивно, т.е. 
матриц А, В, С имеем: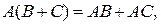 
если определены матрица АВ и В + С.
Доказательство. Пусть . Так как определено АВ, то 
. Так как определено В + С, то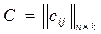 
,
матрица.
матрица.
Пусть, 
тогда
Пусть 
, тогда
Значит матрицы и равны. ■
3. 
матриц А, В, С, (В + С) · А = В · А + С · А, если определены матрицы В · А и В + С.
Доказательство. Аналогично 2.
4. 
матриц А, В, 
если определена матрица АВ.
Доказательство. Докажем, что 
Пусть 
, , тогда и - 
матрицы. 
.
Значит матрицы и равны. ■
Замечание. Умножение матриц в общем случае не коммутативно.
Пример. А =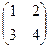 
В = 
АВ = 
ВА = 
АВ≠ВА.