Пусть Р = (Р, +, ·, -, 0, 1)-поле скаляров.  ,
, 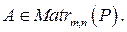
Тогда, 

 -матрица, транспонированная к А.
-матрица, транспонированная к А.
Теорема 1. Для любых матриц А, В, если существует А · В, то  .
.
Доказательство. 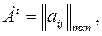

 -
-  матрица
матрица
 -
-  матрица
матрица
 ,
, 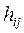 - элемент, расположенный в j -ой строке, i -ом столбце матрицы АВ, значит
- элемент, расположенный в j -ой строке, i -ом столбце матрицы АВ, значит  .
.

 - элемент, расположенный в j -ой строке, i -ом столбце матрицы
- элемент, расположенный в j -ой строке, i -ом столбце матрицы  , значит
, значит  . ■
. ■
Упражнения.
1) Найти сумму матриц:

2) Найти матрицу 2А+5В, если  ,
, 
 ,
,  , 2А+5В
, 2А+5В 
3) Найти произведения матриц АВ и ВА, если
 ,
, 
Решение. АВ= 
ВА= 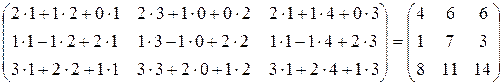
4) Найти 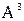 если А=
если А= 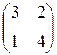
Решение. 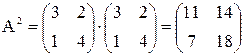

5) Найти значение матричного многочлена 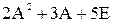
 , Е- единичная матрица третьего порядка.
, Е- единичная матрица третьего порядка.
Решение. 
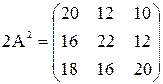 ,
,  ,
, 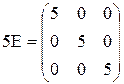

Задачник.
1.Вычислить 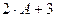 , где
, где  .
.
Решение.

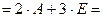
 .
.
2. Вычислите  , где
, где
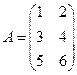 ;
;  .
.
Решение. Так как число столбцов матрицы  равно числу строк матрицы
равно числу строк матрицы  , то произведение
, то произведение  существует (но
существует (но  в этом случае не существует).
в этом случае не существует).
1 способ. По определению произведения матриц:
 .
.
2 способ. Известно, что  -й столбец матрицы
-й столбец матрицы  есть произведение матрицы
есть произведение матрицы  на
на  -й столбец матрицы
-й столбец матрицы 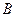 . Поэтому столбцы
. Поэтому столбцы  вычисляем поочередно. Обозначим через
вычисляем поочередно. Обозначим через 
 -ю строку матрицы
-ю строку матрицы  , а через
, а через  -
-  -й столбец матрицы
-й столбец матрицы  . Тогда
. Тогда  . Подробная запись такая:
. Подробная запись такая:
 ;
;
 .
.
Тогда
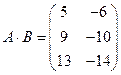 .
.
3 способ. Поскольку  -я строка матрицы
-я строка матрицы  есть произведение
есть произведение  -й строки матрицы
-й строки матрицы  на матрицу
на матрицу 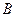 , строки произведения вычисляем поочередно:
, строки произведения вычисляем поочередно:
 ;
;
 ;
;
 .
.
Тогда
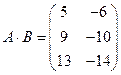 .
.
3. Вычислить  и
и  , если они существуют:
, если они существуют:
а)  ,
,  ;
;
б)  ,
,  ;
;
в)  ,
,  .
.
Решение.
a) 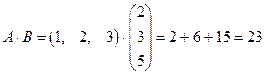 ,
,
 ;
;
б)  ,
,
 ;
;
в)  ,
,  не существует.
не существует.
4.Вычислите  ,
, 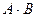 ,
,  ,
,  , если:
, если:
1)  ,
, 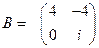 ;
;
2)  ,
,  .
.
5.Вычислите произведения матриц:
1)  ;
;
2)  ;
;
3)  ;
;
4) 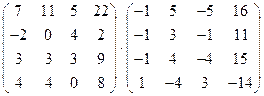 ;
;
5)  ;
;
6)  ;
;
7) 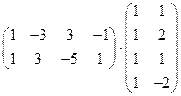 ;
;
8) 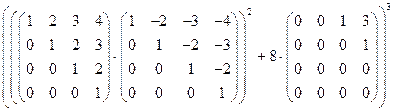 ;
;
9)  ;
;
10) 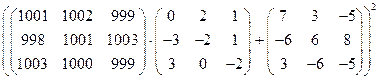 ;
; 
11) 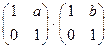 ;
;
12) 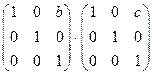 ;
;
13)  ;
;
14)  ;
;
15)  ;
;
16)  ;
;
17) 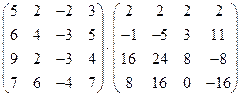 ;
;
18)  ;
;
19) 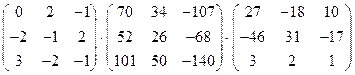 ;
;
20)  .
.
6. Вычислите:
1)  ;
;
2)  .
.
7. Вычислите  и
и  :
:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
, 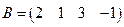 ;
;
4)  ,
,  ;
;
5)  ,
,  ;
;
6)  ,
,  ;
;
7)  ,
,  ;
;
8)  ,
,  .
.
8. Возведите в степень:
1) 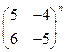 ; 2)
; 2) 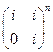 ;
;
3)  ; 4)
; 4) 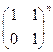 ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8) 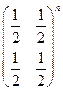 .
.
9. Вычислить обратную матрицу:
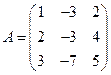 .
.
Решение.



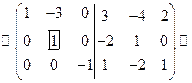

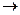

 .
.
10. Вычислить обратные матрицы:
1)  ; 2)
; 2)  ;
;
3) 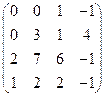 ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  ; 14)
; 14)  ;
;
15)  ;
;
16)  ;
;
17)  ;
;
18)  .
.
11. Решить матричные уравнения вида AX = B:
1)  ; 2)
; 2) 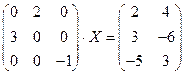 ;
;
3)  ; 4)
; 4)  ;
;
5) 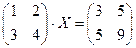 ;
;
6)  ;
;
7)  ; 8)
; 8)  ;
; 
9) 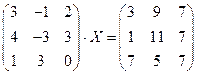 ;
;
10)  .
.
Решение.
5)  ;
;
Вычислим  :
:

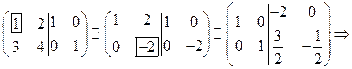
 ,
,
Тогда  :
:
 .
.

12. Решить матричные уравнения вида  :
:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ;
;
6)  ;
;
7) 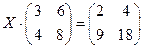 .
.
Решение.
5)  ,
,

 ,
,

 .
. 
13.. Решить матричные уравнения вида  :
:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  .
.
Решение.
 .
.
1) 


 ,
,
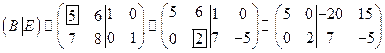


 ,
,
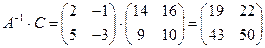 ,
,
 .
.
2) 


 ,
,



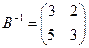 ,
,
 ,
,
 .
.
14. Решите матричные уравнения:
а)  ; б)
; б)  ; в)
; в) 
1)  ,
,  ,
, 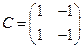 ;
;
2)  ,
,  ,
,  ;
;
3)  ,
,  ,
,  ;
;
4)  ,
,  ,
,  ;
;
5)  ,
,  ,
,  .
.
15. Вычислите 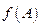 , если:
, если:
1)  ,
, 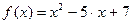 ;
;
2)  ,
,  ;
;
3)  ,
, 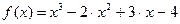 .
.
16. Вычислить 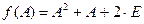 , где
, где  – единичная матрица:
– единичная матрица:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  .
.
17. Привести к диагональной форме путем элементарных преобразований:
1)  ; 2)
; 2)  ;
;
3)  ;
; 
 4)
4)  ;
;
5) 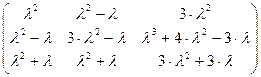 ;
;
6)  ; 7)
; 7)  ;
;
8)  .
.
18. Системы уравнений записать в матричном виде и решить их «методом обратной матрицы»:
1) 
2) 
3) 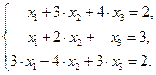
19. Вычислить определители матриц:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4) 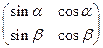 ;
;
6)  ;
;
7)  ; 8)
; 8)  ;
;
9) 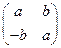 ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13) 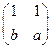 ; 14)
; 14)  ;
;
15)  .
.
Решение.
1)  .
.
3)  .
.
20. Найти определитель разложением по строке:
 .
.
Решение.
Разложим по элементам первой строки:


 .
.
21. Вычислить определители правилом «звездочка»:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ;
;
6)  ; 7)
; 7) 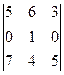 ;
;
8)  ; 9)
; 9)  ;
;
10)  .
.
Решение.
6)  .
.
7)  .
.
22. Вычислить определители, пользуясь только определением:
1)  ; 2)
; 2)  ;
;
3) 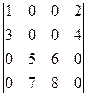 ; 4)
; 4)  ;
;
5)  ;
;
6) 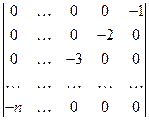 ;
;
7)  ;
;
8) 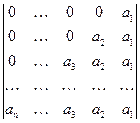 ;
;
9)  ; 10)
; 10)  .
.
23. Дан определитель

Разложите: а) по первому столбцу (строке);
б) по последнему столбцу (строке).
24. Разложите следующие определители:
1)  по элементам 4-го столбца;
по элементам 4-го столбца;
2)  по элементам 1-го столбца;
по элементам 1-го столбца;
3) 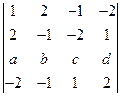 по элементам 3-й строки.
по элементам 3-й строки.
25. Вычислить определители:
1) 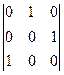 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 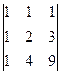 ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12) 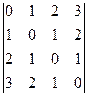 ;
;
13)  ; 14)
; 14) 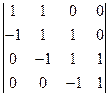 ;
;
15)  ; 16)
; 16)  ;
;
17)  ; 18)
; 18)  .
.
26. Вычислить определители:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 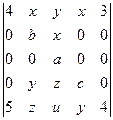 ;
;
7) 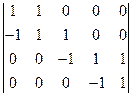 ; 8)
; 8) 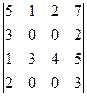 ;
;
9)  ; 10)
; 10) 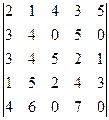 ;
;
11)  ; 11)
; 11)  ;
;
12)  ; 13)
; 13)  .
.
Решение.
1) 



 .
.
27. Вычислить определитель
 .
.
Решение.
1 способ.
Применяя свойства определителей, получим нули в первой строке. Для этого нужно вычесть из второго столбца удвоенный первый, из третьего столбца утроенный первый и т.д.
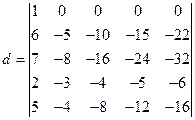 .
.
Разложим по первой строке 
 .
.
Аналогично преобразуем четвертую строку:
 .
.
Определитель равен нулю, так как имеет два пропорциональных столбца.
2 способ.
Вычтем из пятого столбца четвертый, затем из четвертого третий и т. д.:
 .
.
Четвертый и третий столбцы пропорциональны, т.е.  .
.
28. Вычислить определитель
 .
.
Решение.
Вычитаем второй столбец из четвертого и первый из третьего, затем удвоенный первый из второго. Полученный определитель разложим по первой строке:
 .
.
Из третьего столбца полученного определителя вычитаем второй:
 .
.
Разлагаем этот определитель по последнему столбцу:
 .
.
29. Найти решения уравнений:
1) 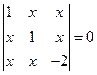 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  .
.
Решение.
2) Вычисляя определитель по правилу «звездочка», получим:
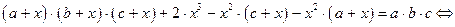


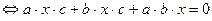

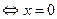 или
или 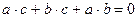 .
.
Тогда
если  , то
, то 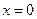 ;
;
если  , то
, то  - любое.
- любое.
30. Найти обратную матрицу  , используя формулу:
, используя формулу: 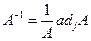
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6)  ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10) 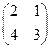 ;
;
11)  12)
12)  ;
;
13)  ; 14)
; 14) 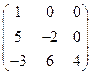 ;
;
15)  ; 16)
; 16)  .
.
Решение.
10) Вычислим определитель матрицы:
 ,
,
Найдем присоединенную матрицу по формуле:
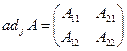 , где
, где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 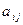 .
.
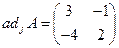 .
.
Тогда
 .
.
15) Найдем определитель матрицы:
 ;
;
Вычислим алгебраические дополнения:
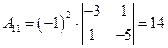 ;
; 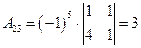 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;
Тогда
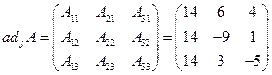 .
.
Следовательно
 .
.
16) Найдем определитель матрицы:
 ;
;
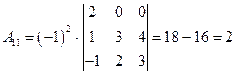 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
; 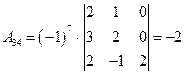 ;
;
 ;
;  ;
;
 ;
;  ;
;
 ;
;  ;
;
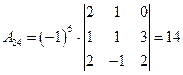 ;
; 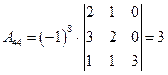 ;
;
 ;
;
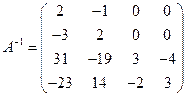 .
.
31. Вычислить определители  -го порядка:
-го порядка:
1)  ;
;
2)  ;
;
3)  .
.
Решение.
1 способ:
1. Приведем определитель к треугольному виду. Тогда он будет равен произведению диагональных элементов. Выполняем преобразования:
а) к первой строке прибавили все строки и результат записали в первой строке;
б) из первой строки определителя вынесли множитель  ;
;
в) вычли первую строку из всех остальных;
получим
 .
.
2 способ:
Обозначим определитель через  . Выразим
. Выразим  через
через  .
.
Первую строку представим как сумму двух строк  . В соответствии с этим разложим
. В соответствии с этим разложим  на сумму двух определителей:
на сумму двух определителей:
 .
.
Первое слагаемое приведем к треугольному виду, вычтя первый столбец из всех остальных. Второе слагаемое после понижения порядка равно  :
:
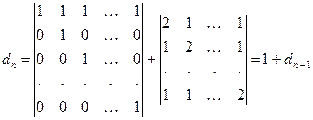 .
.
Получено рекуррентное соотношение 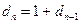 , т.е.
, т.е.  является членом арифметической прогрессии с разностью
является членом арифметической прогрессии с разностью  . Для вычисления некоторого члена этой прогрессии рассмотрим
. Для вычисления некоторого члена этой прогрессии рассмотрим  .
.
Итак,  . Поэтому
. Поэтому  тогда
тогда 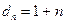 .
.
32. Вычислите коэффициент при  в разложении определителя:
в разложении определителя:
1)  ;
;
2)  .
.
33. Вычислить определители приведением к треугольному виду (всюду, где по виду определителя нельзя узнать его порядок, предполагается, что порядок равен 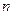 ):
):
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 7)
; 7)  ;
;
8)  .
.
34. Вычислить определители методом представления их в виде суммы (порядок определителей равен 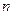 ):
):
1)  ;
;
2) 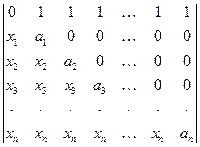 .
.
35. Докажите, что
1)  ;
;
2)  .
.
35. Вычислить определители, представляя их в виде произведений определителей:
1)  ;
;
2)  ;
;
3)  .
.
36. Решить системы уравнений по правилу Крамера:
1) 
2) 
3) 
4) 
5) 
Решение.
1) Найдем определитель системы:
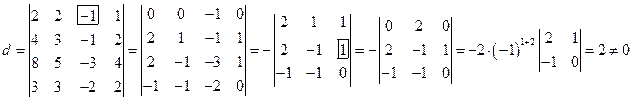 Вычислим определители, заменяя столбцом свободных членов поочередно столбцы основного определителя:
Вычислим определители, заменяя столбцом свободных членов поочередно столбцы основного определителя:
 ;
;
 ;
;
 ;
;
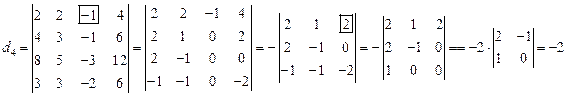 ;
;

Получим  .
.