Эллиптические параболоиды

Лекция 9.

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Лекция 9. Поверхности второго порядка. Цилиндрические поверхности. Поверхности вращения. Эллипсоид. Гиперболоиды. Конус. Параболоиды. Их канонические уравнения. Исследование поверхностей второго порядка методом сечений. Нахождение проекции линии пересечения двух поверхностей на координатную плоскость.

 

Определение. Поверхность второго порядка может быть задана алгебраическим уравнением:

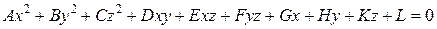или

.

§1.Цилиндрические поверхности.

Рис.83

Теорема 1.

1) Уравнение 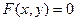определяет цилиндрическую поверхность с образующими, параллельными оси Oz и с направляющей

(1).

(То есть, уравнение цилиндра, образующие которого параллельны оси Oz, имеют вид 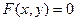, т.е. не содержат координату z.)

2) Уравнение 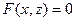определяет цилиндрическую поверхность с образующими, параллельными оси Oу и с направляющей

 

(2).

3) Уравнение 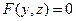определяет цилиндрическую поверхность с образующими, параллельными оси Oу и с направляющей

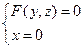(3).

Доказательство.

Докажем первое утверждение теоремы.

 

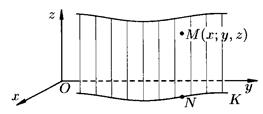Рис. 84.

Пусть в плоскости О х у лежит некоторая линия K, уравнение которой:

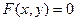. (12.21).

Построим цилиндр с образующими параллельными оси Oz,направляющей K.

Утверждения 2) и 3) теоремы 1 доказываются аналогично.

 

Эллиптический цилиндр. Параболический цилиндр.

 

 

 

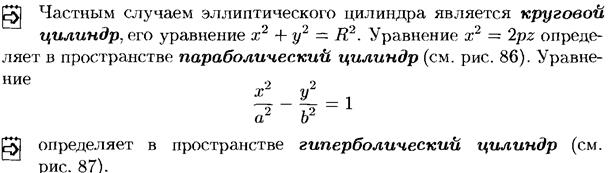
Гиперболический цилиндр.

 

 

 

Замечание. Основные типы цилиндров второго порядка см.

Методические рекомендации: О.А. Бархатова, Г.С. Садыхов.

Поверхности второго порядка. –Таблица 1, стр.9-11.

Преобразование сжатия. Под преобразованием сжатия к координатной плоско­сти xOz мы понимаем такое преобразование, при котором точка M(x; y; z) смещается в точку M'(x; y/k; z), k > 0. Параметр k называют коэффициентом сжатия. При k > 1 точки пространства, расположенные на одной прямой, перпендикулярной плоскости xOz, в резуль­тате такого преобразования сближаются, т.е. преобразование — действительно сжатие. При 0 < k < 1 преобразование фактически является растяжением.

Пусть в пространстве в прямоугольной системе координат Oxyz некоторое множество Q задано своим уравнением F(x,y,z) = 0. При преобразовании сжатия к координатной плоско­сти xOz с коэффициентом k это множество превратится в новое множество Q¹ с уравнением F(x,ky,z) = 0. Это следует из того, что точка (x; y; z) тогда и только тогда принадлежит множеству Q¹, когда точка (x; ky; z) принадлежит множеству Q.

Поверхности вращения. Канонические уравнения поверхностей второго порядка.

Определение. Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в её плоскости, называется поверхностью вращения.

Правило.

Чтобы найти уравнение поверхности, образованной вращением линии, принадлежащей координатной плоскости, вокруг координатной оси этой плоскости, нужно в уравнении линии оставить без изменения переменную, соответствующую оси вращения, а другую переменную заменить квадратным корнем из суммы квадратов этой переменной и переменной, не входящей в уравнение линии.

Пример 1.

Пусть плоская кривая: задана в полуплоскости . Поверхность образована вращением этой кривой вокруг оси Ox. Чтобы составить уравнение этой поверхности, нужно в уравнении кривой оставить без изменения , а вместо 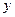подставить . Получаем уравнение поверхности вращения вокруг оси Ох в виде .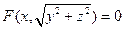

Пример 2. Рассмотрим эллипс 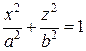, ось вращения Oz. В соответствии с правилом, заменим х на 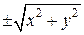и получим поверхность вращения - эллипсоид вращения с осью вращения Oz, который описывается уравнением:

(.)

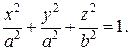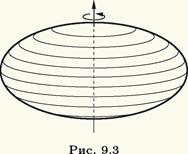Определение. Поверхность, которая получается при вращении эллипса вокруг одной из его осей симме­трии, называют эллипсоидом вращения.

Определение. Уравнение: 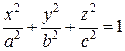задаёт поверхность второго порядка и называется каноническим уравнением эллипсоида. Три параметра a, b и с, входящие в него — это полуоси эллипсо­ида. Если все три полуоси эллипсоида попарно различны, то эллипсоид называют

трехосным.

При совпадении каких-либо двух полуосей (как, например, в уравнении (.)) эллипсоид является поверхностью вращения (эллипсоидом вращения). Если равны все три полуоси (a=b=c=r), то эллипсоид превращается в сферу, которая описывается уравнением: х² + у² + z² = r².

Замечание. Уравнение (.) приводится к каноническому уравнению эллипсоида преобразованием сжатия. (Преобразование сжатия – см. стр 81, лекц. 9 Крищенко А.П.).

Гиперболоиды

При вращении гиперболы вокруг одной из ее осей симметрии получается поверхность, назы­ваемая гиперболоидом вращения. Выбор оси вращения влияет на тип гиперболоида. Если осью вращения является действительная ось симметрии гиперболы, то поверхность вращения будет состоять из двух частей (полостей). Это двуполостный гиперболоид вращения (рис. 9.6). При вращении гиперболы вокруг ее мнимой оси симметрии поверхность будет состоять из одной полости (рис. 9.7). Такую поверхность называют однополостным ги­перболоидом вращения.

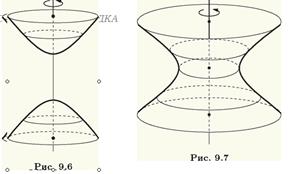
Двуполостный Однополостный

гиперболоид гиперболоид

вращения вращения

Определение. Уравнение: называется каноническим уравнением двуполостного гиперболоида.

Уравнение: 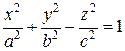называется каноническим уравнением однополостного гиперболоида.

 

Двуполостный Однополостный

гиперболоид гиперболоид

вращения вращения

Пример 3. Для случая двуполостного гиперболоида вращения гипербола задаётся уравнением: ,

ось вращения Oz (ось симметрии гиперболы).

В соответствии с правилом, заменим х на и получим поверхность вращения: - уравнение двуполостного гиперболоида вращения.

Для случая однополостного гиперболоида вращения гипербола задаётся уравнением: , ось вращения Oz (ось симметрии гиперболы). В соответствии с правилом, заменим х на и получим поверхность вращения: - уравнение однополостного гиперболоида вращения.

Замечание. Уравнениягиперболоидов вращения преобразованием сжатия к координатной плоскости хОz превращаются в канонические уравнения гиперболоидов.

Эллиптические параболоиды

При вращении параболы вокруг её оси получаем параболоид вращения.

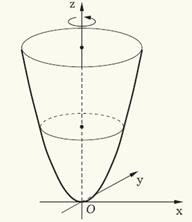
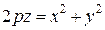Что­бы найти его уравнение, выберем прямоугольную систему координат, направив ось Oz по оси вращения и совместив координатную плоскость xOz с плоскостью параболы. Пусть при этом парабола описывается уравнением x² = 2pz, p > 0. Тогда для получения уравнения поверхно­сти вращения нужно заменить в этом уравнении х на . Тогда получим - уравнение параболоида вращения.

Определение. Уравнение: называется каноническим уравнением эллиптического параболоида, (который является поверхностью второго порядка)

При a=b он превращается в параболоид вращения.

Замечание. Уравнениепараболоида вращения преобразованием сжатия к координатной плоскости хОz превращается в каноническое уравнение эллиптического параболоида.

Конусы

При вращении прямой L, пересекающейся с осью вращения, образуется прямой круго­вой конус. Точка пересечения вращающейся прямой с осью вращения остается неподвижной, ее называют вершиной конуса.

 

Уравнение будем выводить в прямоугольной системе координат, ось Oz кото­рой совпадает с осью вращения, а начало системы координат — с вершиной конуса. Ось Ox расположим так, чтобы прямая L находилась в координатной плоскости xOz и описывалась уравнением z = k₁x. В этой системе координат уравнение поверхности вращения получается из уравнения прямой заменой х на 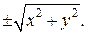В результате такой замены

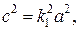получаем Возведя уравнение в квадрат, придём к соотношению разделив его на получим - каноническое уравнение прямого кругового конуса.

Определение. Уравнение 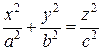называется каноническим уравнением эллиптического конуса.

Эл­липтический конус при а = b совпадает с прямым круговым конусом, и оба они являются поверхностями второго порядка.

Замечание. Преобразование сжатия прямого кругового конуса к координатной плоскости xOz с коэффициентом k даёт эллиптический конус.

Пример 4. Вращая прямую вокруг оси 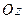, получим поверхность

вращения (её уравнение или ).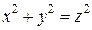

Она называется конусом второго порядка.

Пример 5. (Из типового расчёта). Написать уравнение поверхности, полученной при вращении заданной кривой вокруг заданной оси. Сделать рисунок.

Дано: 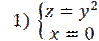, ось вращения - Oz

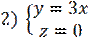, ось вращения - Ox

Решение:

1)

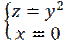
z - не меняется, т.к. вокруг оси Oz совершается вращение

― параболоид вращения.

2) ось вращения - Ox

 

x – не меняется, т.к. вокруг оси Ox совершается вращение

Тогда

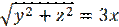
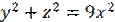
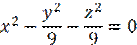
―Конус с центром в точке (0; 0; 0)